|
ГЛАВНАЯ
> Вернуться к содержанию
Кибернетика и программирование
Правильная ссылка на статью:
Вавилов В.А.
Анализ функционирующих в полумарковской среде RQ-систем с возвратом заявок
// Кибернетика и программирование.
2019. № 1.
С. 18-36.
DOI: 10.25136/2644-5522.2019.1.28838 URL: https://nbpublish.com/library_read_article.php?id=28838
Анализ функционирующих в полумарковской среде RQ-систем с возвратом заявок
Вавилов Вячеслав Анатольевич
кандидат физико-математических наук
доцент, кафедра программной инженерии, Национальный исследовательский Томский государственный университет
634050, Россия, Томская область, г. Томск, ул. Ленина, 36
Vavilov Viacheslav
PhD in Physics and Mathematics
Associate Professor, Department of Software Engineering, National Research Tomsk State University
634050, Russia, Tomskaya oblast', g. Tomsk, ul. Lenina, 36

|
vavilovv@yandex.ru
|
|
 |
Другие публикации этого автора
|
|
|
DOI: 10.25136/2644-5522.2019.1.28838
Дата направления статьи в редакцию:
01-02-2019
Дата публикации:
04-03-2019
Аннотация:
Объектом исследования данной работы являются RQ-системы (retrial queueing systems, системы с повторными вызовами) с простейший входящим потоком требований, ожиданием на орбите, возвратом заявок и функционированием в случайной (полумарковской) среде. Рассматриваемые системы являются моделями широкого класса реальных систем обслуживания, в которых заявка по завершении успешного обслуживания может покинуть систему навсегда или через некоторый промежуток времени вернуться в систему для повторного обслуживания. Примерами таких систем являются банки, где выплативший кредит клиент может повторно обратиться за новым кредитом, центры занятости, где клиенты могут обращаться повторно в поисках новой работы и т. п. Эффективность функционирования таких систем зависит от ряда факторов, характер влияния которых можно определить как случайный (случайная полумарковская среда). В данной работе проводится математическое моделирование изучаемого класса систем. Инструментом исследования рассматриваемых систем является математический аппарат теории массового обслуживания. Предложенная математическая модель RQ-систем с возвратом заявок в полумарковской среде исследуется методом асимптотического анализа марковизируемых систем. Научная новизна работы заключается в том, что впервые предложена математическая модель функционирующей в полумарковской среде RQ-системы с вызываемыми заявками и проведён её асимптотический анализ. Найдено асимптотическое среднее нормированного числа заявок в системе, величины отклонения от среднего, получена основная вероятностно-временная характеристика – плотность распределения вероятностей значений процесса изменения состояний системы.
Ключевые слова:
система массового обслуживания, орбита, случайная среда, полумарковский процесс, метод асимптотического анализа, диффузионная аппроксимация, диффузионный процесс, цепь Маркова, переменные параметры, простейший поток заявок
Abstract: The object of this research is RQ-systems (retrial queueing systems, systems with repeated calls) with the simplest incoming flow of requirements, waiting in orbit, return of requests and functioning in a random (semi-Markov) environment. The systems in question are models of a wide class of real service systems in which an application, upon completion of a successful service, can leave the system permanently or, after a certain period of time, return to the system for repeated maintenance. Examples of such systems are banks, where a customer who has repaid a loan can reapply for a new loan, employment centers, where customers can reapply in search of new work, etc. The efficiency of such systems depends on a number of factors, the nature of which can be defined as random (random semi-Markov environment). In this article, the author presents a mathematical modeling of the class of systems under study. The research tool of the systems under consideration is the mathematical apparatus of the theory of mass service. The proposed mathematical model of RQ-systems with the return of applications in a semi-Markov medium is investigated by the method of asymptotic analysis of markovized systems. The scientific novelty of the work lies in the fact that for the first time a mathematical model of an RQ-system functioning in a semi-Markovian environment with called applications was proposed and its asymptotic analysis was performed. The asymptotic average of the normalized number of customers in the system, the deviation from the average is found, the main probability-time characteristic is obtained - the probability density distribution of the values of the process of changing the system states.
Keywords: queuing system, orbit, random environment, semi-Markov process, asymptotic analysis method, diffusion approximation, diffusion process, Markov chain, variable parameters, Poisson flow of applications
1. Введение
Основным средством исследования стохастических систем являются марковские процессы [1-7]. Марковские цепи накладывают определённые ограничение на исследуемые процессы, что обусловлено требованием перехода из одного состояния марковской цепи в другое в каждый единичный промежуток времени. Если же снять это ограничение и допустить произвольное распределение времени пребывания в данном состоянии, то получится полумарковский процесс [4-6, 8-11], являющийся обобщением марковских процессов.
Необходимость оптимизации сетей связи, математическими моделями которых являются системы массового обслуживания, привела к рассмотрению управляемых систем массового обслуживания [12-15]. По-другому такие системы называют системами с переменными параметрами. Таким системам посвящены работы Коротаева И. А. [16-21].
Изменение параметров может происходить как внутри системы в зависимости от ее состояния, так и под воздействием внешних условий, например изменения случайной среды, в которой и функционирует система. В работе [22] представлены исследования систем массового обслуживания со случайной интенсивностью входящего пуассоновского потока.
Впервые понятие дважды стохастического входящего потока было введено Кингманом [23]. Системы массового обслуживания с входящим дважды стохастическим пуассоновским потоком не сводятся к классическим системам массового обслуживания с постоянными параметрами, поскольку входящий поток в данном случае не является рекуррентным.
Можно рассматривать задачу, когда изменяются не только параметры входящего потока, но и параметры обслуживания. Такие системы принято называть системами массового обслуживания, функционирующими в случайной среде [24-25]. Впервые понятие система, функционирующая в случайной среде, появилось в работе [26].
Соответствующие исследования применительно не только к системам массового обслуживания, но и к сетям связи представлены в трудах Дудина А.Н. [27-30], Neuts M.P. [31], Sztrick J. [32], Takahashi H., Akimaru H. A [33]. Возможные значения параметров систем массового обслуживания связываются со значениями некоторого случайного процесса, который называют управляющим процессом. Изменения значений управляющего процесса приводит к изменению параметров функционирования системы.
В связи с тем, что получение точных выражений для вычисления требуемых вероятностно-временных характеристик является достаточно сложной задачей, возникло направление решения задач теории массового обслуживания с помощью асимптотических методов [10, 34-37]. Эти методы позволяют отойти от явной разрешимости с использованием диффузионных процессов.
В ряде работ при анализе систем массового обслуживания, функционирующих в случайной среде, применяется метод диффузионной аппроксимации. В этом случае задача сводится к анализу характеристик диффузионного процесса с изменяющимися в случайные моменты времени коэффициентами переноса и диффузии. Плотности распределения можно найти из системы дифференциальных уравнений Фоккера-Планка. Такой подход используется в [38-43].
Особый интерес в последнее время представляет исследование RQ-систем (retrial queueing systems, системы с повторными вызовами), которые являются адекватными моделями широкого класса технических и социально-экономических систем [43-50]. Так, например, в работе [44] приводится более семи сотен ссылок на работы данной направленности. Тем не менее, исследованию RQ-систем, функционирующих в случайной среде, уделяется недостаточно внимания. В наших работах представлены RQ-системы, где в качестве математической модели случайной среды рассмотрена цепь Маркова [46-47], полумарковский процесс [48-49], диффузионный процесс [50].
В данной работе предлагается математическая модель RQ-систем с возвратом заявок и функционированием в полумарковской среде, проводится асимптотическое исследование.
2. Математическая модель
Рассмотрим RQ-систему, на вход которой поступает простейший с параметром λ поток заявок. Прибор этой системы может находиться в одном из двух состояний: k=0, если он свободен; k=1, если он занят обслуживанием заявки. Заявка, заставшая в момент поступления прибор свободным, начинает обслуживаться с интенсивностью µ. Если в течение обслуживания этой заявки другие требования на прибор не поступают, то исходная заявка по завершении обслуживания покидает систему с вероятностью r или с вероятностью 1-r переходит на орбиту. Если в течение обслуживания одной заявки поступает другая, то поступившая заявка переходит на орбиту. Повторное обращение заявок к прибору из орбиты происходит после случайной задержки, продолжительность которой имеет экспоненциальное распределение с параметром γ. Число заявок на орбите обозначим i.
Система функционирует в случайной среде. В качестве математической модели случайной среды рассмотрим полумарковский процесс s(t) с непрерывным временем t, то есть такой дискретный случайный процесс, который принимает значения из конечного множества состояний s=1,2,...,S и для которого вложенная по моментам времени tn изменения состояний цепь s(tn) является Марковской. Времена пребывания этого процесса в различных состояниях являются условно независимыми случайными величинами, распределение вероятностей значений которых зависит лишь от номера состояния полумарковского процесса.
Для определения полумарковского процесса s(t) зададим стохастическую матрицу одношаговых вероятностей ps1s2 переходов вложенной цепи Маркова
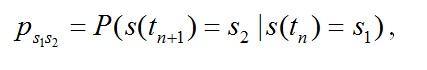
при этом будем полагать, что pss=0.
Понятно, что
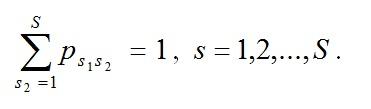
Также зададим набор функций распределения Gs(x) значений времени пребывания полумарковского процесса в s-м состоянии.
Влияние случайной среды на функционирование RQ-системы определяется зависимостью интенсивности µ обслуживания заявок от состояний s(t)=s случайной среды, то есть µ=µ(s), а также зависимостью параметров λ и γ от состояний s(t)=s случайной среды, то есть λ=λ(s), γ=γ(s). Вероятность окончания обслуживания заявки на приборе за бесконечно малый промежуток времени Δt равна µ(s)Δt+o(Δt). Вероятность поступления нового требования в систему за бесконечно малый промежуток времени Δt равна λ(s)Δt+o(Δt). Вероятность обращения заявки на прибор из орбиты за бесконечно малый промежуток времени Δt равна γ(s)Δt+o(Δt).
В силу свойств приведенной математической модели трехмерный случайный вектор {k(t),i(t),s(t)} изменения во времени состояний {k(t),i(t)} RQ-системы и состояний {s(t)} математической модели случайной среды является полумарковским процессом.
Для исследования описанной математической модели марковизируем процесс {k(t),i(t),s(t)} методом дополнительной переменной. Введем переменную ζ(t), имеющую смысл длины интервала времени от момента t до момента смены текущего состояния случайной среды, тогда процесс изменения значений вектора {k(t),i(t),s(t),ζ(t)} является марковским процессом.
Обозначим P(k(t)=k,i(t)=i,s(t)=s, ζ(t)<ζ)=Pk(i,s,ζ,t).
В любой момент времени должно выполняться условие нормировки
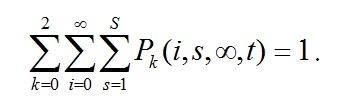
Для распределения Pk(i,s,ζ,t) можно составить систему дифференциальных уравнений Колмогорова:
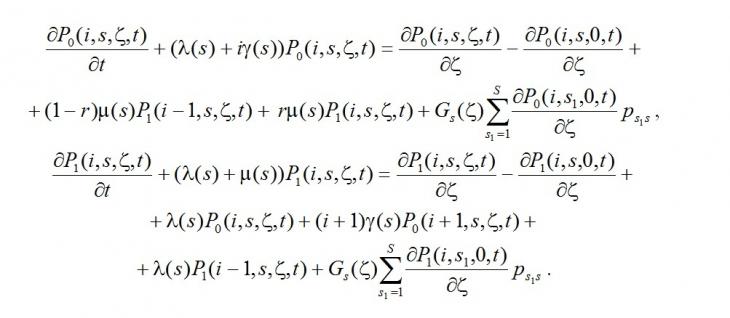
Обозначим γ(s)= γσ(s) и перепишем данную систему в следующем виде
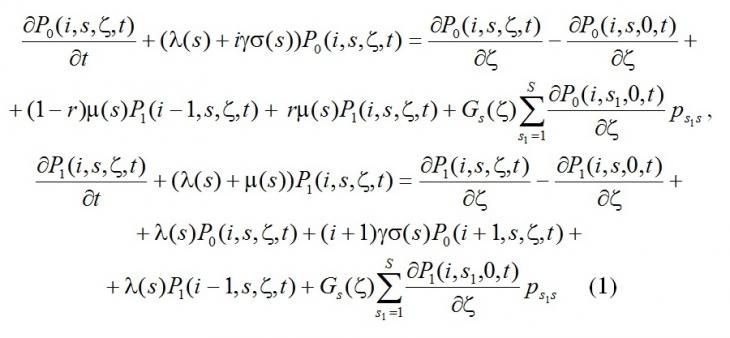
Систему (1) будем исследовать методом асимптотического анализа [40] в условиях большой задержки заявок на орбите γ→0. Для этого в (1) выполним замены:
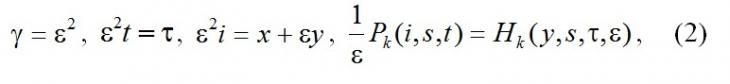
тогда получим
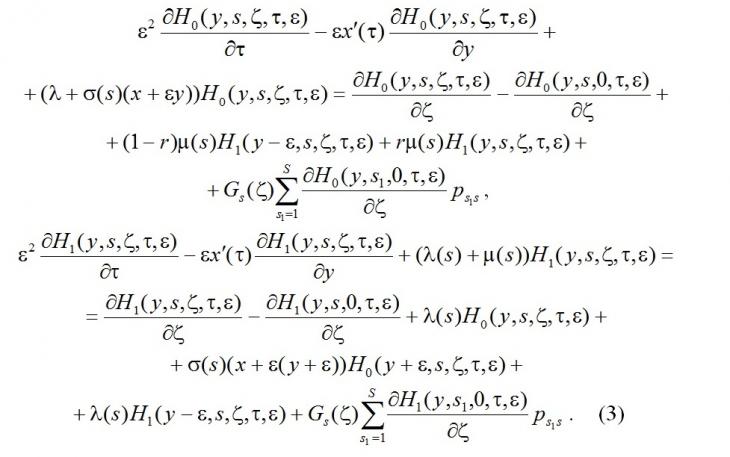
3. Исследование асимптотических средних характеристик
Под асимптотическими средними характеристиками RQ-систем с вызываемыми заявками, будем понимать распределение вероятностей Rk(x) состояний k канала и предельную функцию
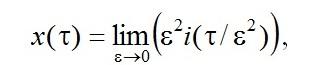
имеющую смысл асимптотического среднего нормированного числа заявок в системе.
В системе (3) перейдем к пределу при ε→0 и, полагая, что существуют конечные пределы
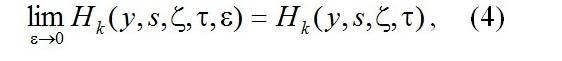
получим систему
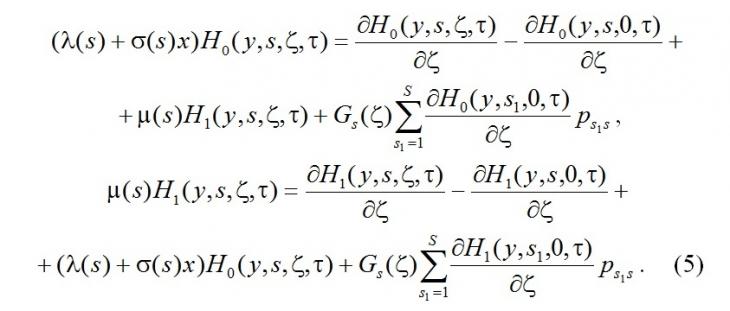
Решение Hk(y,s,ζ,τ) системы (5) будем искать в виде
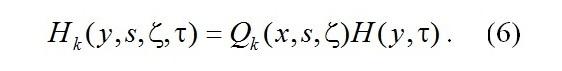
Тогда Qk(x,s,ζ), имеющая смысл условного совместного распределения вероятностей состояний k канала и s среды при условии x(τ)=x определяется системой вида
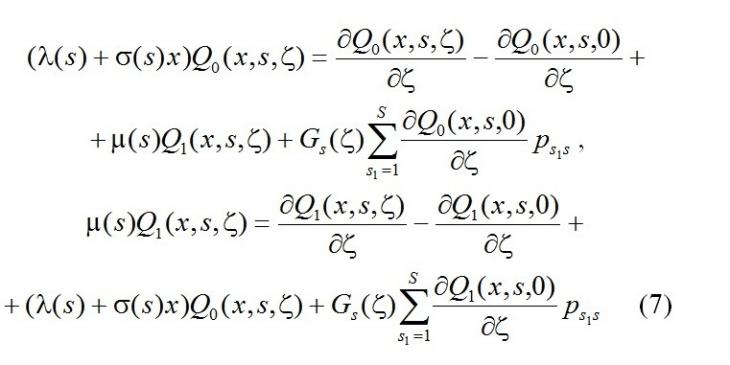
и условием нормировки
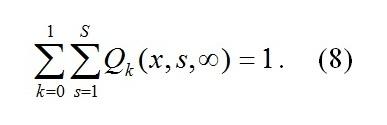
Будем полагать, что Qk(x,s,ζ) известны, если удается каким либо образом решить систему (7).
Далее покажем, что x=x(τ) является детерминированной функцией.
В системе (3) функции Hk(y±ε,s,τ,ε) разложим в ряд по приращениям аргумента y с точностью до o(ε), получим
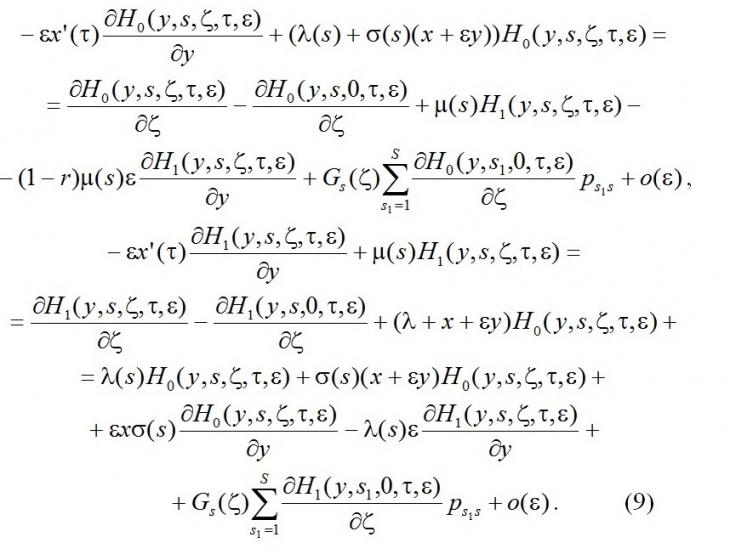
Уравнения системы (9) просуммируем по k и по s, и при ζ→∞ получим
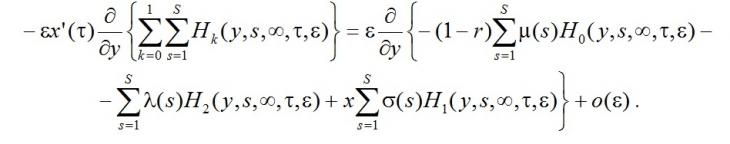
Поделим на ε обе части полученного уравнения, выполним предельный переход (4), учтём (6), получим
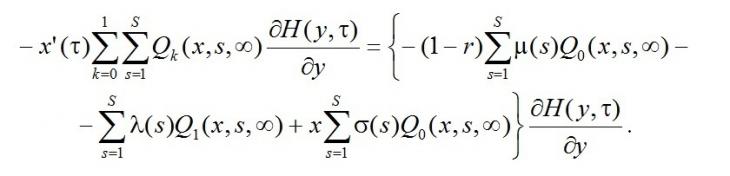
Учтём условие нормировки (8), обозначим
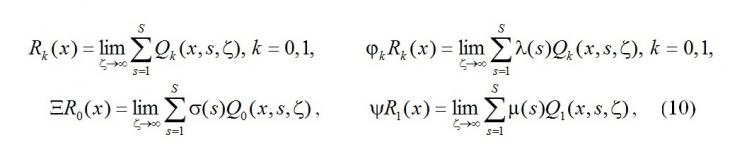
заметим, что Rk(x) имеет смысл распределения вероятностей состояний канала, получим
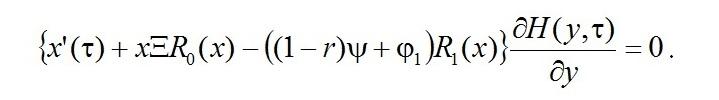
Поскольку производная плотности распределения H(y,τ) не может тождественно равняться нулю, следовательно, функция x=x(τ) является решением обыкновенного дифференциального уравнения
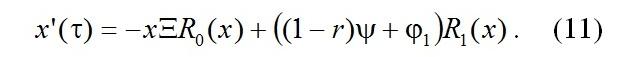
Получили, что x=x(τ) является детерминированной функцией.
4. Величины отклонения нормированного числа заявок в системе от среднего
Рассмотрим процесс
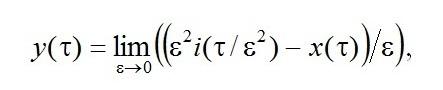
который характеризует изменение величин отклонения нормированного числа заявок в системе от их асимптотического среднего и покажем, что он является диффузионным процессом авторегрессии.
Обозначим
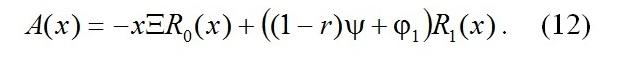
Будем искать решение Hk(y,s,ζ,τ,ε) системы (3) в виде
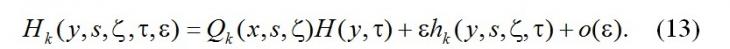
Подставим в систему (9) разложение (13), учтём (7) и запишем полученную систему, сократив на  все уравнения, в следующем виде все уравнения, в следующем виде
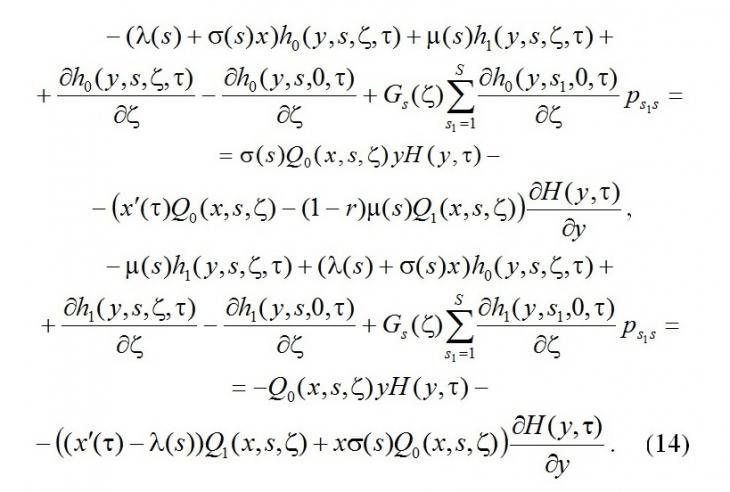
Будем искать решение системы (14) в следующем виде
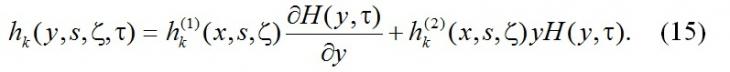
Подставим (15) в (14) и представим систему в виде двух систем
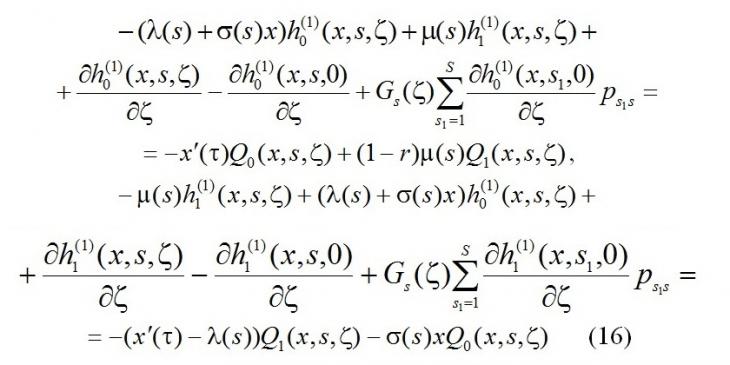
и
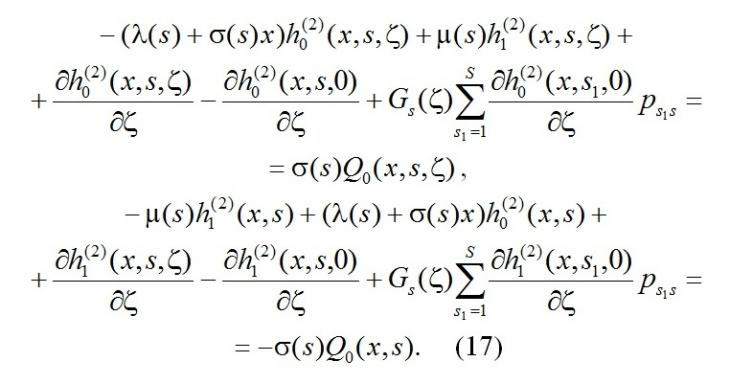
Продифференцируем систему (7) по x, получим
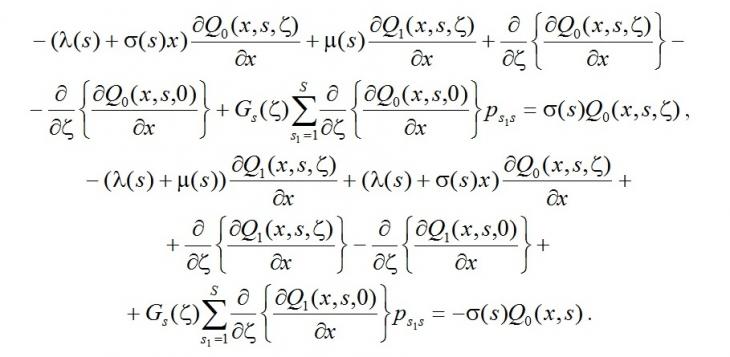
Из последней системы с учётом системы (17) следует, что решение
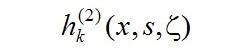
системы (17) имеет вид
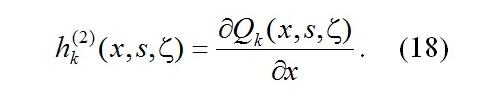
С учётом (18) и (15) разложение (13) примет вид
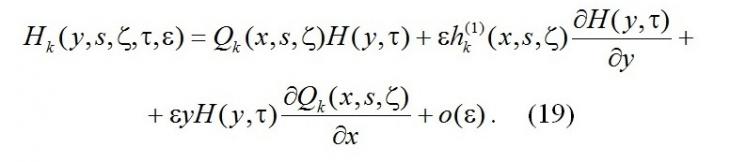
Теперь найдём вид функции H(y,τ). Для этого функции в правой части системы (3) разложим в ряд по приращениям аргумента y с точностью до o(ε2), получим
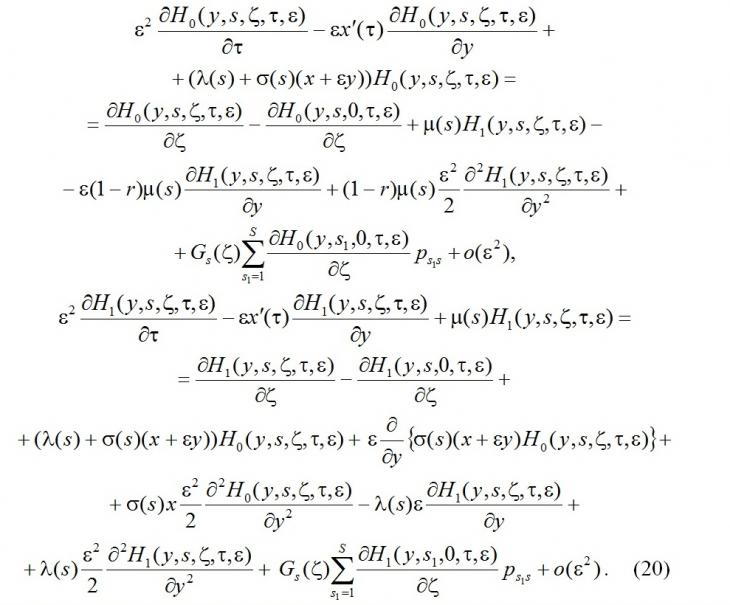
Сложим все уравнения системы (20) по k, получим
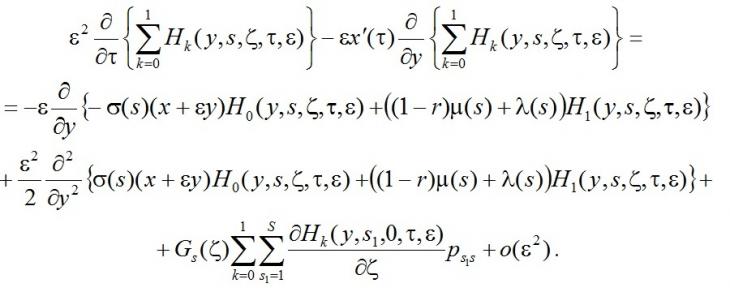
Подставим в полученную систему разложение функций Hk(y,s,ζ,τ,ε) в виде (19), учтём обозначение (10), получим
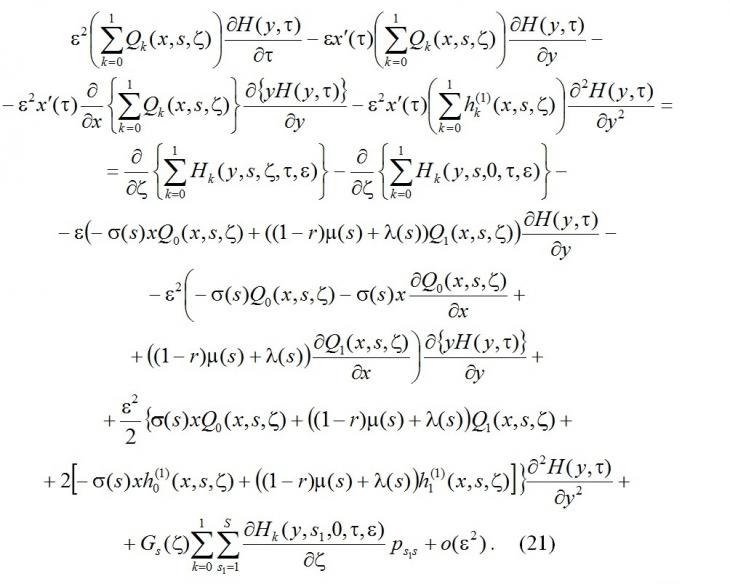
Просуммируем уравнения системы (21) по s, выполним предельный переход при ζ→∞, воспользуемся условием нормировки (8), обозначением (10), также обозначим
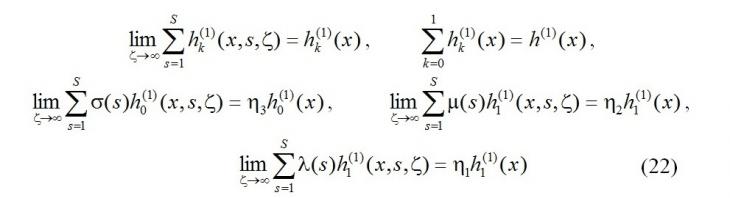
учтём, что
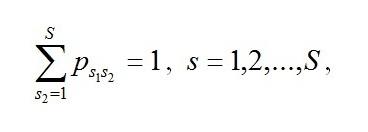
получим
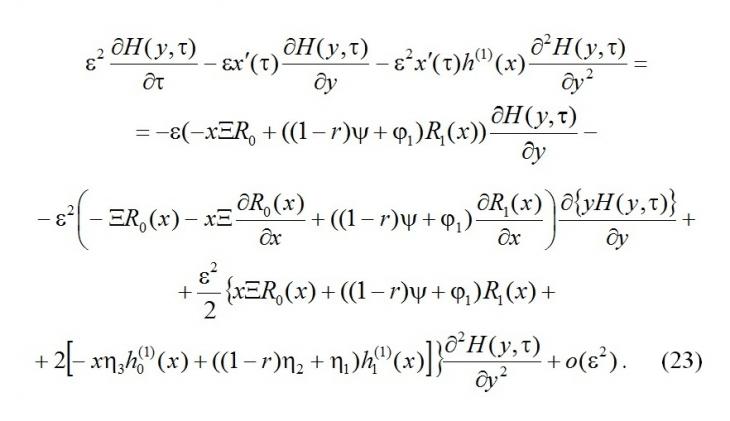
В силу дифференциального уравнения (11) уничтожим в (23) слагаемые порядка o(ε), поделим обе части полученного уравнения на ε2, выполним преобразования, будем иметь
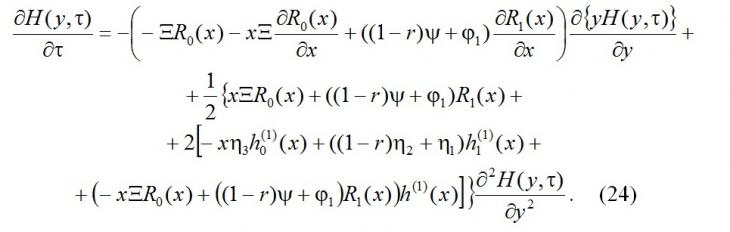
Получили уравнение Фоккера – Планка для плотности распределения вероятностей H(y,τ) значений диффузионного процесса авторегрессии y(τ). Заметим, что коэффициент переноса уравнения (24) есть производная по x от правой части дифференциального уравнения (11). В силу обозначения (12) можно записать
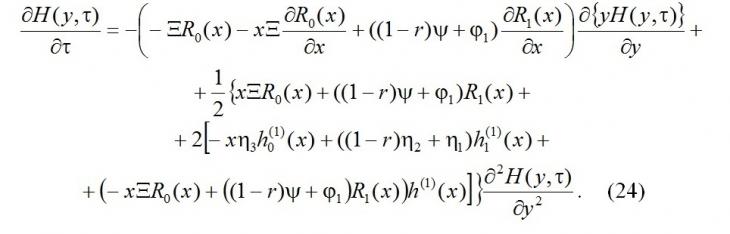
Коэффициент диффузии с учётом (24) обозначим следующим образом
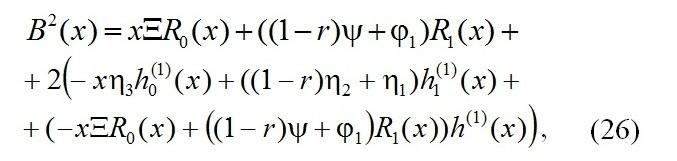
если выражение в правой части больше нуля.
Из (24) следует, что H(y,τ) является плотностью распределения вероятностей диффузионного процесса y(τ), который удовлетворяет стохастическому дифференциальному уравнению
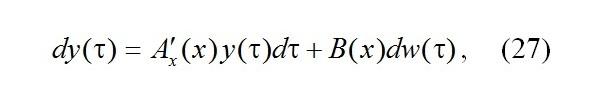
где w(τ) является стандартным процессом Винера, то есть y(τ) является процессом авторегрессии.
5. Плотность распределения вероятностей процесса изменения состояний RQ-системы
Используя предельные процессы x(τ) и y(τ) для достаточно малых значений параметра ε, рассмотрим процесс z(τ)=x(τ)+εy, который аппроксимирует процесс изменения числа заявок в системе ε2i(τ/ε2) и покажем, что он является однородным диффузионным процессом.
Дифференцируя z(τ) по τ получаем dz(τ)=x'(τ)dτ+εdy.
В силу (11) и (12) имеем
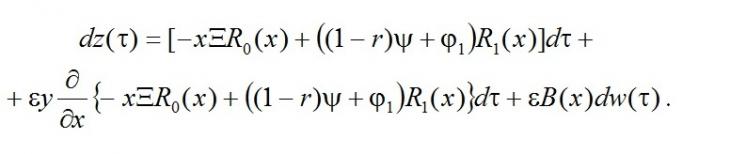
Так как правая часть содержит разложение в ряд по приращениям εy аргументаx, то можно записать
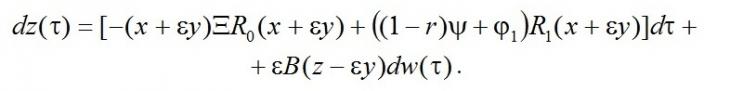
С точностью до o(ε), имеем
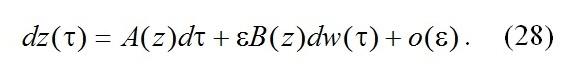
Обозначим F(z,τ) плотность распределения вероятностей значений процесса z(τ), тогда можно записать уравнение Фоккера – Планка для плотности этого процесса
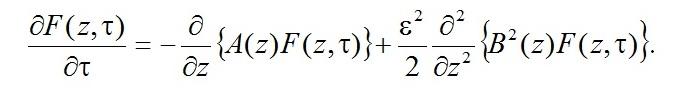
Рассмотрим функционирование процесса z(τ) в стационарном режиме, то есть F(z,τ)=F(z), тогда стабильное распределение можно найти из уравнения Фоккера – Планка
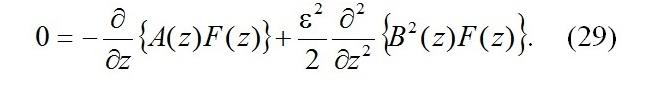
Уравнение (29) является однородным дифференциальным уравнением второго порядка и имеет решение:
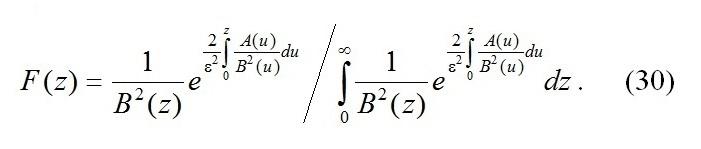
6. Выводы
Таким образом, в данной работе предложена математическая модель функционирующей в полумарковской среде RQ-системы с вызываемыми заявками. Методом асимптотического анализа [8] получено обыкновенное дифференциальное уравнение (11), определяющее асимптотическое среднее x=x(τ) нормированного числа заявок в системе. Представлено распределение Rk(x), k=0,1, вероятностей состояний прибора в виде (10), где величины Qk(x,s,ζ), k=0,1, имеющие смысл условного совместного распределения вероятностей состояний k канала и состояний s полумарковской среды, определяются системой уравнений вида (7). Показано, что процесс y(τ), характеризующий изменение величин отклонения нормированного числа заявок в системе от их асимптотического среднего, является диффузионным процессом авторегрессии и определяется стохастическим дифференциальным уравнением вида (27). Показано, что для достаточно малых значений параметра ε процесс z(τ)=x(τ)+εy, является однородным диффузионным процессом. Найдена важнейшая вероятностно-временная характеристика процесса z(τ) – плотность распределения вероятностей его значений в виде (30).
Библиография
1. Баруча-Рид А. Г. Теория марковских процессов и ее приложения. – М.: Наука, 1969. – 511 с.
2. Гнеденко Б. В., Коваленко И. Н. Введение в теорию массового обслуживания. – М.: Наука, 1987. – 336 с.
3. Жожикашвили В. А., Вишневский В. М. Сети массового обслуживания. Теория и применения к сетям ЭВМ. – М.: Радио и связь, 1988. – 192 с.
4. Клейнрок Л. Теория массового обслуживания. – М.: Машиностроение, 1979. – 432 с.
5. Матвеев В. Ф.; Ушаков В. Г. Системы массового обслуживания. – М.: Изд-во МГУ 1984. – 240 с.
6. Саати Т. Элементы теории массового обслуживания и ее приложения. – М.: Сов. радио, 1971. – 520 с.
7. Франкен П., Кениг Д., Арндт У., Шмидт Ф. Очереди и точечные процессы: Пер. с англ. – Киев: Наукова думка, 1984. – 284 с.
8. Апанасович В. В., Коледа А. А., Чернявский А. Ф. Статистический анализ случайных потоков в физическом эксперименте. – Минск: Университетское, 1988. – 254 с.
9. Башарин Г. П., Бочаров П. П., Коган Я. А. Анализ очередей в вычислительных сетях. Теория и методы расчета. – М.: Наука, 1989. – 336 с.
10. Боровков А. А. Асимптотические методы в теории массового обслуживания. – М.: Наука, 1980. – 210 с.
11. Джевелл В. С. Управляемые полумарковские процессы // Кибернетический сборник. – М.: Мир, 1967. Вып. 4. – С. 97-137.
12. Головко Н. И., Коротаев И. А. Приближенный расчет средней длины очереди в системах массового обслуживания с переменной интенсивностью входящего потока // Управляемые системы массового обслуживания. – Томск, 1986. Вып. 4. – С. 28-34.
13. Коротаев И. А. Системы массового обслуживания с переменными параметрами. – Томск: Изд-во Том. ун-та, 1991. – 167 с.
14. Назаров А. А. Управляемые системы массового обслуживания и их оптимизация. – Томск: Изд-во Том. ун-та, 1984. – 234 с.
15. Рыков В. В. Управляемые системы массового обслуживания // Теория вероятностей. Математическая статистика. Теоретическая кибернетика, 1975. Т.12. С. 43-154.
16. Головко Н. И., Коротаев И. А. Анализ некоторых систем массового обслуживания с переменной интенсивностью входящего потока // Поиск сигнала в многоканальных системах. – Томск, 1987. Вып. 2. – С. 65-76.
17. Головко Н. И., Коротаев И. А. Время задержки сообщения в узле сети при переменной интенсивности входящего потока // Автоматика и вычислительная техника, 1989. №2. С. 36-39.
18. Головко Н. И., Коротаев И. А. О времени задержки сообщения в узле сети при переменной интенсивности входящего потока // Вычислительные сети коммутации пакетов. Рига: ИЭВТ, 1987. Т.1. С. 107-111.
19. Коротаев И. А. Системы массового обслуживания с переменными параметрами. – Томск: Изд-во Том. ун-та, 1991. – 167 с.
20. Коротаев И. А. Приближенный расчет средней длины очереди в адаптирующихся системах массового обслуживания с переменной интенсивностью обслуживания // Управляемые системы массового обслуживания. – Томск, 1984. Вып. 3. С. 50-57.
21. Коротаев И. А., Терпугов А. Ф. Приближенный расчет характеристик адаптирующихся многолинейных систем массового обслуживания со вспомогательными приборами // Автоматика и вычислительная техника, 1982. №6. – С. 61-65.
22. Каспарсон В. А. Об обслуживании пуассоновского потока требований со случайной интенсивностью // Известия АН СССР. Техническая кибернетика, 1969. №6. С. 52-57.
23. Kingman J. F. On doubly stochastic Poisson process // Proceedings of Cambridge Philosophical Society. 1964. Vol. 60. #4. P. 923-930.
24. Дудин А. Н., Клименок В. И. Расчет характеристик однолинейной системы обслуживания, функционирующей в Марковской синхронной случайной среде // Автоматика и телемеханика, 1997. № 1. С. 74-84.
25. Коган Я. А., Литвин В. Г. К вычислению характеристик системы массового обслуживания с конечным буфером, работающей в случайной среде // Автоматика и телемеханика, 1976. № 12. С. 49-57.
26. Purdue P. The M/M/1 queue in a Markovian environment // Operations Research, 1974. Vol. 22. #3. P. 562-569.
27. Дудин А. Н. Об обслуживающей системе с переменным режимом работы // Автоматика и вычислительная техника, 1985. №2. С. 27-29.
28. Дудин А. Н., Клименок В. И. Расчет характеристик однолинейной системы обслуживания, функционирующей в Марковской синхронной случайной среде // Автоматика и телемеханика, 1997. № 1. С. 74-84.
29. Дудин А. Н. Оптимальное гистерезисное управление ненадежной системой BMAP/SM/1 с двумя режимами работы // Автоматика и телемеханика, 2002. №11. С. 58-73.
30. Dudin A. N. About queuing system operating in the random environment // Izvestia of USSR Academy of Sciences. Technical Cybernetics, 1985. С. 64-78.
31. Neuts M. P. Further results of the M/M/1 queue with randomly varying rates // Opsearch. 1978. Vol. 15. #4. P. 139-157.
32. Sztrick J. On the heterogeneous M/G/N blocking system in a random environment // Journal of Operations Research Society. 1987. Vol. 38. #1. P. 57-63.
33. Takahashi H., Akimaru H. A diffusion model for queues in a randomly varying environment // The Transactions of The IECE of Japan. 1986. Vol. E69. #1. P. 13-20.
34. Анисимов В. В., Закусило О. К., Донченко В. С. Элементы теории массового обслуживания и асимптотического анализа систем. – Киев: Вища школа, 1987. – 248 с.
35. Добрушин Р. Л., Прелов В. В. Асимптотический подход к исследованию сетей коммутации сообщений линейной структуры с большим числом узлов // Проблемы передачи информации. – 1979. Т.15. №1. – С. 61-73.
36. Коган Я. А., Нерсесян С. Г. Асимптотические методы анализа замкнутых сетей в условиях большой загрузки // Автоматика и телемеханика, 1984. №8. – С. 93-103.
37. Назаров А. А. Асимптотический анализ многолинейных систем массового обслуживания с повторными вызовами // Автоматика и вычислительная техника, 1990. №3. С. 65-71.
38. Коган Я. А., Литвин В. Г. К вычислению характеристик системы массового обслуживания с конечным буфером, работающей в случайной среде // Автоматика и телемеханика, 1976. №12. С. 49-57.
39. Kogan Ya. A., Litvin V. G. Piesewise diffusion approximations for queuing problems with heterogeneous arrivals and service // Problem of Operation and Theory Information, 1979. Vol. 8. #5-6. P. 133-143.
40. Назаров А. А., Моисеева С. П. Метод асимптотического анализа в теории массового обслуживания. – Томск: Изд-во НТЛ, 2006. – 112 с.
41. Гарайшина И. Р., Моисеева С. П., Назаров А. А. Методы исследования коррелированных потоков и специальных систем массового обслуживания. – Томск: Изд-во НТЛ, 2010. – 204 с.
42. Моисеев А. Н., Назаров А. А. Бесконечнолинейные системы и сети массового обслуживания. – Томск: Изд-во НТЛ, 2015. – 240 с.
43. Пауль С. В., Назаров А. А., Анализ RQ-системы M/GI/GI/1/1 с вызываемыми заявками, ненадёжным прибором и дообслуживанием прерванных заявок // Информационные технологии и математическое моделирование (ИТММ-2018): Материалы XVII Международной конференции имени А. Ф. Терпугова (10-15 сентября 2018 г.) – Томск: Изд-во НТЛ, 2018. – С. 139-145.
44. Artalejo J. R., Gomez-Corral A. Retrial Queueing Systems: A Computational Approach. Springer, Heidelberg, 2008.
45. Вавилов В. А. Исследование одноканальной системы с повторными вызовами // Методы прогнозирования в технике и технологиях: сборник статей Международной научно-практической конференции (г. Тюмень, 20 февраля 2018 г.). В 2 ч. Ч. 2. – Уфа: Аэтерна, 2018. – С. 6-13.
46. Вавилов В. А. Исследование немарковских RQ-систем, функционирующих в случайной среде // Современные концепции научных исследований: ежемесячный научный журнал. – М.: ЕСУ, 2014. – № 5 (13). – С. 56-59.
47. Вавилов В. А. Исследование RQ-систем в условиях возрастающего количества абонентских станций // Информационные технологии и математическое моделирование (ИТММ-2012): Материалы XI Всероссийской научно-практической конференции с международным участием (23-24 ноября 2012 г.) – Кемерово, 2012. Ч. 2. С. 80-85.
48. Вавилов В. А., Назаров А. А. Исследование RQ-систем в полумарковской среде // Международная конференция "Теория вероятностей и ее приложения", посвященная 100-летию со дня рождения Б. В. Гнеденко. – Москва: Ленанд, 2012. – С. 180-183.
49. Вавилов В. А. Исследование RQ-систем, функционирующих в полумарковской среде // Вестник Кемеровского госуниверситета. – Кемерово: Изд-во КемГУ, 2014. – № 3 (59). Т. 3. – С. 99-106.
50. Вавилов В. А. Математическое моделирование неустойчивых сетей случайного доступа в диффузионной среде при дважды стохастическом входящем потоке // Вестник Томского госуниверситета. Управление, вычислительная техника и информатика. Научный журнал. – Томск: Изд-во НТЛ, 2009. – № 2 (7). C. 31-51.
References
1. Barucha-Rid A. G. Teoriya markovskikh protsessov i ee prilozheniya. – M.: Nauka, 1969. – 511 s.
2. Gnedenko B. V., Kovalenko I. N. Vvedenie v teoriyu massovogo obsluzhivaniya. – M.: Nauka, 1987. – 336 s.
3. Zhozhikashvili V. A., Vishnevskii V. M. Seti massovogo obsluzhivaniya. Teoriya i primeneniya k setyam EVM. – M.: Radio i svyaz', 1988. – 192 s.
4. Kleinrok L. Teoriya massovogo obsluzhivaniya. – M.: Mashinostroenie, 1979. – 432 s.
5. Matveev V. F.; Ushakov V. G. Sistemy massovogo obsluzhivaniya. – M.: Izd-vo MGU 1984. – 240 s.
6. Saati T. Elementy teorii massovogo obsluzhivaniya i ee prilozheniya. – M.: Sov. radio, 1971. – 520 s.
7. Franken P., Kenig D., Arndt U., Shmidt F. Ocheredi i tochechnye protsessy: Per. s angl. – Kiev: Naukova dumka, 1984. – 284 s.
8. Apanasovich V. V., Koleda A. A., Chernyavskii A. F. Statisticheskii analiz sluchainykh potokov v fizicheskom eksperimente. – Minsk: Universitetskoe, 1988. – 254 s.
9. Basharin G. P., Bocharov P. P., Kogan Ya. A. Analiz ocheredei v vychislitel'nykh setyakh. Teoriya i metody rascheta. – M.: Nauka, 1989. – 336 s.
10. Borovkov A. A. Asimptoticheskie metody v teorii massovogo obsluzhivaniya. – M.: Nauka, 1980. – 210 s.
11. Dzhevell V. S. Upravlyaemye polumarkovskie protsessy // Kiberneticheskii sbornik. – M.: Mir, 1967. Vyp. 4. – S. 97-137.
12. Golovko N. I., Korotaev I. A. Priblizhennyi raschet srednei dliny ocheredi v sistemakh massovogo obsluzhivaniya s peremennoi intensivnost'yu vkhodyashchego potoka // Upravlyaemye sistemy massovogo obsluzhivaniya. – Tomsk, 1986. Vyp. 4. – S. 28-34.
13. Korotaev I. A. Sistemy massovogo obsluzhivaniya s peremennymi parametrami. – Tomsk: Izd-vo Tom. un-ta, 1991. – 167 s.
14. Nazarov A. A. Upravlyaemye sistemy massovogo obsluzhivaniya i ikh optimizatsiya. – Tomsk: Izd-vo Tom. un-ta, 1984. – 234 s.
15. Rykov V. V. Upravlyaemye sistemy massovogo obsluzhivaniya // Teoriya veroyatnostei. Matematicheskaya statistika. Teoreticheskaya kibernetika, 1975. T.12. S. 43-154.
16. Golovko N. I., Korotaev I. A. Analiz nekotorykh sistem massovogo obsluzhivaniya s peremennoi intensivnost'yu vkhodyashchego potoka // Poisk signala v mnogokanal'nykh sistemakh. – Tomsk, 1987. Vyp. 2. – S. 65-76.
17. Golovko N. I., Korotaev I. A. Vremya zaderzhki soobshcheniya v uzle seti pri peremennoi intensivnosti vkhodyashchego potoka // Avtomatika i vychislitel'naya tekhnika, 1989. №2. S. 36-39.
18. Golovko N. I., Korotaev I. A. O vremeni zaderzhki soobshcheniya v uzle seti pri peremennoi intensivnosti vkhodyashchego potoka // Vychislitel'nye seti kommutatsii paketov. Riga: IEVT, 1987. T.1. S. 107-111.
19. Korotaev I. A. Sistemy massovogo obsluzhivaniya s peremennymi parametrami. – Tomsk: Izd-vo Tom. un-ta, 1991. – 167 s.
20. Korotaev I. A. Priblizhennyi raschet srednei dliny ocheredi v adaptiruyushchikhsya sistemakh massovogo obsluzhivaniya s peremennoi intensivnost'yu obsluzhivaniya // Upravlyaemye sistemy massovogo obsluzhivaniya. – Tomsk, 1984. Vyp. 3. S. 50-57.
21. Korotaev I. A., Terpugov A. F. Priblizhennyi raschet kharakteristik adaptiruyushchikhsya mnogolineinykh sistem massovogo obsluzhivaniya so vspomogatel'nymi priborami // Avtomatika i vychislitel'naya tekhnika, 1982. №6. – S. 61-65.
22. Kasparson V. A. Ob obsluzhivanii puassonovskogo potoka trebovanii so sluchainoi intensivnost'yu // Izvestiya AN SSSR. Tekhnicheskaya kibernetika, 1969. №6. S. 52-57.
23. Kingman J. F. On doubly stochastic Poisson process // Proceedings of Cambridge Philosophical Society. 1964. Vol. 60. #4. P. 923-930.
24. Dudin A. N., Klimenok V. I. Raschet kharakteristik odnolineinoi sistemy obsluzhivaniya, funktsioniruyushchei v Markovskoi sinkhronnoi sluchainoi srede // Avtomatika i telemekhanika, 1997. № 1. S. 74-84.
25. Kogan Ya. A., Litvin V. G. K vychisleniyu kharakteristik sistemy massovogo obsluzhivaniya s konechnym buferom, rabotayushchei v sluchainoi srede // Avtomatika i telemekhanika, 1976. № 12. S. 49-57.
26. Purdue P. The M/M/1 queue in a Markovian environment // Operations Research, 1974. Vol. 22. #3. P. 562-569.
27. Dudin A. N. Ob obsluzhivayushchei sisteme s peremennym rezhimom raboty // Avtomatika i vychislitel'naya tekhnika, 1985. №2. S. 27-29.
28. Dudin A. N., Klimenok V. I. Raschet kharakteristik odnolineinoi sistemy obsluzhivaniya, funktsioniruyushchei v Markovskoi sinkhronnoi sluchainoi srede // Avtomatika i telemekhanika, 1997. № 1. S. 74-84.
29. Dudin A. N. Optimal'noe gisterezisnoe upravlenie nenadezhnoi sistemoi BMAP/SM/1 s dvumya rezhimami raboty // Avtomatika i telemekhanika, 2002. №11. S. 58-73.
30. Dudin A. N. About queuing system operating in the random environment // Izvestia of USSR Academy of Sciences. Technical Cybernetics, 1985. S. 64-78.
31. Neuts M. P. Further results of the M/M/1 queue with randomly varying rates // Opsearch. 1978. Vol. 15. #4. P. 139-157.
32. Sztrick J. On the heterogeneous M/G/N blocking system in a random environment // Journal of Operations Research Society. 1987. Vol. 38. #1. P. 57-63.
33. Takahashi H., Akimaru H. A diffusion model for queues in a randomly varying environment // The Transactions of The IECE of Japan. 1986. Vol. E69. #1. P. 13-20.
34. Anisimov V. V., Zakusilo O. K., Donchenko V. S. Elementy teorii massovogo obsluzhivaniya i asimptoticheskogo analiza sistem. – Kiev: Vishcha shkola, 1987. – 248 s.
35. Dobrushin R. L., Prelov V. V. Asimptoticheskii podkhod k issledovaniyu setei kommutatsii soobshchenii lineinoi struktury s bol'shim chislom uzlov // Problemy peredachi informatsii. – 1979. T.15. №1. – S. 61-73.
36. Kogan Ya. A., Nersesyan S. G. Asimptoticheskie metody analiza zamknutykh setei v usloviyakh bol'shoi zagruzki // Avtomatika i telemekhanika, 1984. №8. – S. 93-103.
37. Nazarov A. A. Asimptoticheskii analiz mnogolineinykh sistem massovogo obsluzhivaniya s povtornymi vyzovami // Avtomatika i vychislitel'naya tekhnika, 1990. №3. S. 65-71.
38. Kogan Ya. A., Litvin V. G. K vychisleniyu kharakteristik sistemy massovogo obsluzhivaniya s konechnym buferom, rabotayushchei v sluchainoi srede // Avtomatika i telemekhanika, 1976. №12. S. 49-57.
39. Kogan Ya. A., Litvin V. G. Piesewise diffusion approximations for queuing problems with heterogeneous arrivals and service // Problem of Operation and Theory Information, 1979. Vol. 8. #5-6. P. 133-143.
40. Nazarov A. A., Moiseeva S. P. Metod asimptoticheskogo analiza v teorii massovogo obsluzhivaniya. – Tomsk: Izd-vo NTL, 2006. – 112 s.
41. Garaishina I. R., Moiseeva S. P., Nazarov A. A. Metody issledovaniya korrelirovannykh potokov i spetsial'nykh sistem massovogo obsluzhivaniya. – Tomsk: Izd-vo NTL, 2010. – 204 s.
42. Moiseev A. N., Nazarov A. A. Beskonechnolineinye sistemy i seti massovogo obsluzhivaniya. – Tomsk: Izd-vo NTL, 2015. – 240 s.
43. Paul' S. V., Nazarov A. A., Analiz RQ-sistemy M/GI/GI/1/1 s vyzyvaemymi zayavkami, nenadezhnym priborom i doobsluzhivaniem prervannykh zayavok // Informatsionnye tekhnologii i matematicheskoe modelirovanie (ITMM-2018): Materialy XVII Mezhdunarodnoi konferentsii imeni A. F. Terpugova (10-15 sentyabrya 2018 g.) – Tomsk: Izd-vo NTL, 2018. – S. 139-145.
44. Artalejo J. R., Gomez-Corral A. Retrial Queueing Systems: A Computational Approach. Springer, Heidelberg, 2008.
45. Vavilov V. A. Issledovanie odnokanal'noi sistemy s povtornymi vyzovami // Metody prognozirovaniya v tekhnike i tekhnologiyakh: sbornik statei Mezhdunarodnoi nauchno-prakticheskoi konferentsii (g. Tyumen', 20 fevralya 2018 g.). V 2 ch. Ch. 2. – Ufa: Aeterna, 2018. – S. 6-13.
46. Vavilov V. A. Issledovanie nemarkovskikh RQ-sistem, funktsioniruyushchikh v sluchainoi srede // Sovremennye kontseptsii nauchnykh issledovanii: ezhemesyachnyi nauchnyi zhurnal. – M.: ESU, 2014. – № 5 (13). – S. 56-59.
47. Vavilov V. A. Issledovanie RQ-sistem v usloviyakh vozrastayushchego kolichestva abonentskikh stantsii // Informatsionnye tekhnologii i matematicheskoe modelirovanie (ITMM-2012): Materialy XI Vserossiiskoi nauchno-prakticheskoi konferentsii s mezhdunarodnym uchastiem (23-24 noyabrya 2012 g.) – Kemerovo, 2012. Ch. 2. S. 80-85.
48. Vavilov V. A., Nazarov A. A. Issledovanie RQ-sistem v polumarkovskoi srede // Mezhdunarodnaya konferentsiya "Teoriya veroyatnostei i ee prilozheniya", posvyashchennaya 100-letiyu so dnya rozhdeniya B. V. Gnedenko. – Moskva: Lenand, 2012. – S. 180-183.
49. Vavilov V. A. Issledovanie RQ-sistem, funktsioniruyushchikh v polumarkovskoi srede // Vestnik Kemerovskogo gosuniversiteta. – Kemerovo: Izd-vo KemGU, 2014. – № 3 (59). T. 3. – S. 99-106.
50. Vavilov V. A. Matematicheskoe modelirovanie neustoichivykh setei sluchainogo dostupa v diffuzionnoi srede pri dvazhdy stokhasticheskom vkhodyashchem potoke // Vestnik Tomskogo gosuniversiteta. Upravlenie, vychislitel'naya tekhnika i informatika. Nauchnyi zhurnal. – Tomsk: Izd-vo NTL, 2009. – № 2 (7). C. 31-51.
Результаты процедуры рецензирования статьи
В связи с политикой двойного слепого рецензирования личность рецензента не раскрывается.
Со списком рецензентов издательства можно ознакомиться здесь.
Предмет исследования – разработка асимптотической математической модели RQ-систем (retrial queueing systems, системы с повторными вызовами) с возвратом заявок, функционирующих в полумарковской среде.
Методология исследования основана на сочетании теоретического и модельного подходов с применением методов анализа, моделирования, сравнения, обобщения, синтеза.
Актуальность исследования обусловлена широким применением систем массового обслуживания в различных отраслях современной экономики и, соответственно, необходимостью их изучения и моделирования в целях повышения эффективности, включая системы с повторными вызовами с возвратом заявок, функционирующие в полумарковской среде.
Научная новизна связана с обоснованием автором математической модели функционирующей в полумарковской среде RQ-системы с вызываемыми заявками.
Стиль изложения научный. Статья написана русским литературным языком.
Структура рукописи включает следующие разделы: 1. Введение (средства исследования стохастических систем, марковские процессы, марковские цепи, полумарковский процесс, управляемые системы массового обслуживания / системы с переменными параметрами, изменение параметров внутри системы и под воздействием внешних условий, понятие дважды стохастического входящего потока, системы массового обслуживания, функционирующие в случайной среде, направление решения задач теории массового обслуживания с помощью асимптотических методов, метод диффузионной аппроксимации, система дифференциальных уравнений Фоккера-Планка, исследование RQ-систем (retrial queueing systems, системы с повторными вызовами), математическая модель RQ-систем с возвратом заявок и функционированием в полумарковской среде), 2. Математическая модель (RQ-система, на вход которой поступает простейший с параметром λ поток заявок, в случайной среде, полумарковский процесс s (t ) с непрерывным временем t , определение полумарковского процесса s (t ), стохастическая матрица одношаговых вероятностей p s1s2 переходов вложенной цепи Маркова, набор функций распределения G s(x ) значений времени пребывания полумарковского процесса в s -м состоянии, зависимость интенсивности µ обслуживания заявок от состояний s (t )=s случайной среды, марковизация процесса {k (t ),i (t ),s (t )} методом дополнительной переменной, система дифференциальных уравнений Колмогорова), 3. Исследование асимптотических средних характеристик (распределение вероятностей R k(x ) состояний k канала, предельная функция, имеющая смысл асимптотического среднего нормированного числа заявок в системе, условное совместное распределение вероятностей состояний k канала и s среды при условии x (τ)=x (детерминированная функция)), 4. Величины отклонения нормированного числа заявок в системе от среднего (изменение величин отклонения нормированного числа заявок в системе от их асимптотического среднего, уравнение Фоккера-Планка для плотности распределения вероятностей H (y ,τ) значений диффузионного процесса авторегрессии y (τ)), 5. Плотность распределения вероятностей процесса изменения состояний RQ-системы (предельные процессы x (τ) и y (τ) для достаточно малых значений параметра ε, процесс z (τ)=x (τ)+εy , который аппроксимирует процесс изменения числа заявок в системе ε2i (τ/ε2) – однородный диффузионный процесс), 6. Выводы (заключение), Библиография.
Разделы «Введение», «Выводы» нумеровать не следует. Текст, предшествующий формулам, завершается двоеточием. В разделе «Введение» нужно указать инициалы учёного Кингмана.
Содержание в целом соответствует названию. В то же время желательно скорректировать формулировку заголовка, исключив из неё аббревиатуру RQ, например: «Анализ функционирующих в полумарковской среде систем с повторными вызовами с возвратом заявок». Желательно указать области практического применения разработанной модели, представить подтверждение её эффективности.
Библиография включает 49 источников отечественных и зарубежных авторов – монографии, научные статьи, материалы научных мероприятий. Библиографические описания некоторых источников нуждаются в корректировке в соответствии с ГОСТ и требованиями редакции, например:
5. Матвеев В. Ф., Ушаков В. Г. Системы массового обслуживания. – М. : Изд-во Моск. ун-та, 1984. – 240 с.
11. Джевелл В. С. Управляемые полумарковские процессы // Кибернетический сборник. – М. : Мир, 1967. – Вып. 4. – С. 97–137.
17. Головко Н. И., Коротаев И. А. Время задержки сообщения в узле сети при переменной интенсивности входящего потока // Автоматика и вычислительная техника. – 1989. – № 2. – С. 36–39.
18. Головко Н. И., Коротаев И. А. О времени задержки сообщения в узле сети при переменной интенсивности входящего потока // Вычислительные сети коммутации пакетов. – Рига : ИЭВТ, 1987. – Т. 1. – С. 107–111.
23. Kingman J. F. On doubly stochastic Poisson process // Proceedings of Cambridge Philosophical Society. – 1964. – Vol. 60. – № 4. – P. 923–930.
43. Пауль С. В., Назаров А. А., Анализ RQ-системы M/GI/GI/1/1 с вызываемыми заявками, ненадёжным прибором и дообслуживанием прерванных заявок // Информационные технологии и математическое моделирование (ИТММ-2018) : материалы XVII Международной конференции имени А. Ф. Терпугова (10–15 сентября 2018 г.) – Томск : Изд-во НТЛ, 2018. – С. 139–145.
44. Artalejo J. R., Gomez-Corral A. Retrial Queueing Systems: A Computational Approach. – Heidelberg : Springer, 2008. – ??? р.
45. Вавилов В. А. Исследование одноканальной системы с повторными вызовами // Методы прогнозирования в технике и технологиях : сборник статей Международной научно-практической конференции (г. Тюмень, 20 февраля 2018 г.) : в 2 ч. – Уфа : Аэтерна, 2018. – Ч. 2. – С. 6–13.
49. Вавилов В. А. Исследование RQ-систем, функционирующих в полумарковской среде // Вестник Кемеровского госуниверситета. – 2014. – № 3 (59). – Т. 3. – С. 99–106.
50. Вавилов В. А. Математическое моделирование неустойчивых сетей случайного доступа в диффузионной среде при дважды стохастическом входящем потоке // Вестник Томского госуниверситета. Управление, вычислительная техника и информатика. – 2009. – № 2 (7). – C. 31–51.
Источники №№ 13, 19 идентичны, что следует исправить. Возможно излишнее самоцитирование (Коротаев И. А., Вавилов В. А., Назаров А. А. с соавторами).
Апелляция к оппонентам (Гнеденко Б. В., Коваленко И. Н., Жожикашвили В. А., Вишневский В. М., Клейнрок Л., Матвеев В. Ф.; Ушаков В. Г., Апанасович В. В., Коледа А. А., Чернявский А. Ф., Башарин Г. П., Бочаров П. П., Коган Я. А., Боровков А. А., Рыков В. В., Каспарсон В. А., Дудин А. Н., Клименок В. И., Коган Я. А., Литвин В. Г., Дудин А. Н., Клименок В. И., Анисимов В. В., Закусило О. К., Донченко В. С., Добрушин Р. Л., Прелов В. В., Нерсесян С. Г., Коган Я. А., Литвин В. Г., Моисеева С. П., Гарайшина И. Р., Баруча-Рид А. Г., Саати Т.,Франкен П., Кениг Д., Арндт У., Шмидт Ф., Джевелл В. С., Пауль С. В., Artalejo J. R., Gomez-Corral A., Neuts M. P., Sztrick J., Takahashi H., Akimaru H., Purdue P., Kingman J. F. и др.) имеет место.
В целом рукопись соответствует основным требованиям, предъявляемым к научным статьям. Материал представляет интерес для читательской аудитории и после доработки может быть опубликован в журнале «Кибернетика и программирование» (рубрика «Математическое моделирование и вычислительный эксперимент»).
Ссылка на эту статью
Просто выделите и скопируйте ссылку на эту статью в буфер обмена. Вы можете также
попробовать найти похожие
статьи
|
|





