|
ГЛАВНАЯ
> Вернуться к содержанию
Кибернетика и программирование
Правильная ссылка на статью:
Катасёв А.С.
Нейронечеткая модель формирования правил классификации, как эффективный аппроксиматор объектов с дискретным выходом
// Кибернетика и программирование.
2018. № 6.
С. 110-122.
DOI: 10.25136/2644-5522.2018.6.28081 URL: https://nbpublish.com/library_read_article.php?id=28081
Нейронечеткая модель формирования правил классификации, как эффективный аппроксиматор объектов с дискретным выходом
Катасёв Алексей Сергеевич
кандидат технических наук
доцент кафедры систем информационной безопасности Казанского национального исследовательского технического университета им. А.Н. Туполева-КАИ
420111, Россия, Республика Татарстан, г. Казань, ул. К. Маркса, 10
Katasev Alexey Sergeevich
PhD in Technical Science
Associate Professor of Information Security Systems Department of the Tupolev Kazan National Research Technical University
420111, Russia, respublika Tatarstan, g. Kazan', ul. K.marksa, 10

|
Kat_726@mail.ru
|
|
 |
Другие публикации этого автора
|
|
|
DOI: 10.25136/2644-5522.2018.6.28081
Дата направления статьи в редакцию:
21-11-2018
Дата публикации:
15-01-2019
Аннотация:
Предметом исследования данной статьи является оценка эффективности аппроксимации объектов с дискретным выходом на основе нечетких баз знаний. Объектом исследования является нейронечеткая модель, позволяющая на основе обучения нечеткой нейронной сети формировать систему нечетко-продукционных правил (нечеткую базу знаний) для оценки состояния объектов. Автор подробно рассматривает предложенный им вид нечетко-продукционных правил, алгоритм логического вывода на правилах, описывает разработанную модель нечеткой нейронной сети. Особое внимание уделяется необходимости оценки аппроксимирующей способности модели с целью определения возможности и эффективности ее практического использования. Данная оценка производилась методом анализа следующих характеристик модели: - сходимости разработанного алгоритма обучения нечеткой нейронной сети; - удовлетворения ее работы принципам нечеткой аппроксимации; - непротиворечивости алгоритма логического вывода на правилах модели известному алгоритму аппроксимации объектов с дискретным выходом на основе нечеткой базы знаний. Произведена оценка аппроксимирующей способности нейронечеткой модели, по результатам которой сделан вывод, что данная модель является эффективным аппроксиматором объектов с дискретным выходом. Кроме того, с целью апробации модели проведена оценка классифицирующей способности формируемых нечетких правил. Точность классификации на базе нечетких правил оказалась не ниже точности других известных методов классификации. Практической ценностью применения таких правил является возможность построения систем поддержки принятия решений по оценке состояния объектов в различных предметных областях.
Ключевые слова:
нечеткая нейронная сеть, нейронечеткая модель, нечетко-продукционное правило, аппроксимация, моделирование, оценка состояния объекта, поддержка принятия решений, нечеткая логика, нейронная сеть, нечеткая база знаний
Данная работа выполнена в рамках государственного задания Министерства образования и науки Российской Федерации, проект № 8.6141.2017/8.9.
Abstract: The subject of this research is to evaluate the effectiveness of the approximation of objects with discrete output based on fuzzy knowledge bases. The object of the research is the neuro-fuzzy model, which allows, based on the training of a fuzzy neural network, to form a system of fuzzy-production rules (a fuzzy knowledge base) for assessing the state of objects. The author examines in detail the type of fuzzy-production rules proposed by him, the algorithm of logical inference on the rules, describes the developed model of a fuzzy neural network. Particular attention is paid to the need to assess the approximating ability of the model in order to determine the feasibility and effectiveness of its practical use. This assessment was made by analyzing the following model characteristics:- convergence of the developed learning algorithm for fuzzy neural network;- satisfaction of its work with the principles of fuzzy approximation;- consistency of the logic inference algorithm on the rules of the model to the well-known algorithm for approximating objects with discrete output based on a fuzzy knowledge base. The estimation of the approximating ability of the neuro-fuzzy model was made, based on the results of which it was concluded that this model is an effective approximator of objects with a discrete output. In addition, in order to test the model, an assessment was made of the classifying ability of the fuzzy rules being formed. The accuracy of classification based on fuzzy rules turned out to be no lower than the accuracy of other known classification methods. The practical value of the application of such rules is the ability to build decision support systems for assessing the state of objects in various subject areas.
Keywords: fuzzy neural network, neuro-fuzzy model, fuzzy production rule, approximation, modeling, state object evaluation, decision support, fuzzy logic, neural network, fuzzy knowledge base
Введение
В настоящее время в различных предметных областях возникает необходимость моделирования сложных объектов и систем [19], которые характеризуются следующими особенностями:
- наличием большого числа входов, выходов и состояний;
- разнотипностью входных параметров и нелинейным характером внутренних связей и закономерностей;
- неопределенностью, нечеткостью и неполнотой исходных данных, используемых для моделирования объекта;
- нечеткой выраженностью структуры, которая может изменяться в зависимости от ситуации.
Традиционные подходы, основанные на математической статистике и имитационном моделировании, не всегда позволяют строить адекватные модели объектов в условиях ограниченности временных, вычислительных и материальных ресурсов. Поэтому в настоящее время при решении различных задач, связанных с управлением производственными процессами, распознаванием образов, оценкой состояния объектов, наблюдается повышение научного и практического интереса к методам и моделям искусственного интеллекта с применением технологий интеллектуального анализа данных [1,4,10,12,14].
Теория нечетких множеств, как одно из направлений искусственного интеллекта, позволяет строить нечеткие модели объектов [15]. Методы нечеткой логики и разработанные на ее основе интеллектуальные системы применяются для решения задач оценки состояния объектов [11,18], управления [2,5], поддержки принятия решений [21,23] в различных предметных областях.
Однако, несмотря на достоинства нечетких систем, они имеют существенный недостаток, связанный с необходимостью привлечения человека-эксперта для построения правил базы знаний (БЗ) и задания используемых в них функций принадлежности (ФП). Наиболее сложным этапом построения нечеткой системы является выбор формы и параметров ФП, так как из-за субъективности мнения эксперта построенные им ФП могут не вполне отражать реальную действительность. Кроме того, процесс формулирования нечетких правил и задания ФП требует значительных временных затрат и большой аналитической работы эксперта, что существенно усложняет разработку таких систем.
Для разрешения указанных проблем при разработке интеллектуальных систем актуально применение инструментальных средств, позволяющих автоматически формировать нечеткие правила, адекватно описывающие закономерности в анализируемых данных. В качестве такого средства предлагается специально разработанная нечеткая нейронная сеть (ННС) [6], позволяющая на основе анализа исходных данных формировать систему нечетко-продукционных правил, используемых для оценки состояния объектов.
Вид нечетко-продукционных правил и алгоритм логического вывода на правилах для оценки состояния объектов
Для решения задачи оценки состояния объекта, относящейся к классу задач аппроксимации объектов с дискретным выходом [24], предложен следующий вид нечетко-продукционных правил [8]:
ЕСЛИ x1 = 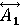 (w1) И x2 = (w1) И x2 =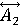 (w2) И … xn = (w2) И … xn =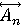 (wn) ТО y =B [CF], (1) (wn) ТО y =B [CF], (1)
где xi – входные параметры, wi – веса условий "xi = 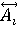 ", ", 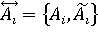 , Ai – четкое значение входа, , Ai – четкое значение входа, 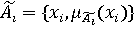 – нечеткое значение входа, – нечеткое значение входа, 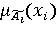 – функция принадлежности, y – выходной параметр, B – четкое значение выхода (состояние объекта), CF – достоверность правила. – функция принадлежности, y – выходной параметр, B – четкое значение выхода (состояние объекта), CF – достоверность правила.
Для определения состояния объекта на основе правил вида (1) разработан алгоритм логического вывода. Введем следующие обозначения:
- R (response) – степень срабатывания условной части правила:
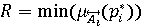 , (2) , (2)
где 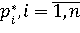 – четкие значения n входных параметров правила (факты), – четкие значения n входных параметров правила (факты),
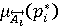 – степени принадлежности входных значений – степени принадлежности входных значений 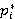 к к 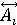 : :
- T (trust) – совокупный вес условной части правила:
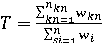 , (3) , (3)
где wi, 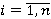 – веса всех ограничений – веса всех ограничений 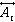 на параметры в правиле, на параметры в правиле,
wkn, 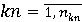 – веса ограничений – веса ограничений 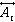 с известными значениями; с известными значениями;
- C (complex) – комплексная оценка достоверности решения правила:
C=R*T*CF, (4)
где CF (certainty factor) – достоверность правила.
С учетом (2)-(4) разработанный алгоритм состоит из следующих этапов.
1. Ввод значений 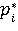 входных параметров в правилах. входных параметров в правилах.
2. Для каждого правила Ruler, 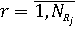 расчет степени срабатывания его условий Rr по формуле (2). расчет степени срабатывания его условий Rr по формуле (2).
3. Формирование конфликтного множества, включающего правила с ненулевой степенью срабатывания: Sconf = {Ruler | Rr ≠ 0}, 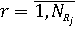 . .
4. Для всех правил RulerÎSconf расчет совокупного веса условной части правила Tr по формуле (3) и комплексной оценки Cr по формуле (4).
5. Разрешение конфликта – выбор правила с максимальной комплексной оценкой достоверности решения: 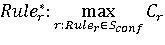 . .
6. Получение значения 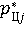 выходного параметра выходного параметра 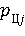 выбранного правила выбранного правила 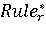 в качестве искомого состояния объекта. в качестве искомого состояния объекта.
Данный алгоритм позволяет на основании сопоставления имеющихся входных данных (фактов) с антецедентами нечетких правил выбрать решающее правило, выходное значение которого определяет искомое состояние объекта.
Описание разработанной нейронечеткой модели
Для формирования системы правил вида (1) разработана нейронечеткая модель, структура которой определяется следующими параметрами:
1) числом входных параметров объекта (определяет число нейронов входного слоя сети);
2) числом значений (градаций) входных параметров объекта (определяет число нейронов слоя значений-градаций входных нейронов сети);
3) числом значений целевого параметра объекта (определяет число нейронов слоя значений выходного нейрона сети);
4) алгоритмом логического вывода на системе правил вида (1) (определяет число слоев сети и их функциональность).
На рисунке 1 приведен пример структуры нечеткой нейронной сети.
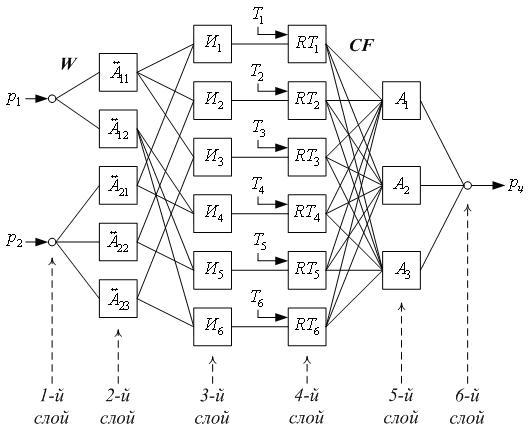
Рис. 1. Пример структуры нечеткой нейронной сети
Первый слой сети состоит из Р-нейронов, выполняющих распределение входных сигналов по нейронам второго слоя сети. Второй слой состоит из 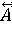 -нейронов, моделирующих входные условия "p= -нейронов, моделирующих входные условия "p=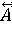 " правил. Выходами " правил. Выходами 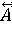 -нейронов являются значения ФП -нейронов являются значения ФП 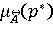 , определяющие степень срабатывания условных частей правил. С каждым , определяющие степень срабатывания условных частей правил. С каждым 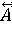 -нейроном связан параметр w, определяющий вес (важность) условия в правиле. Третий слой сети состоит из И-нейронов, определяющих оценку R степени срабатывания условной части правил. В четвертом слое сети вычисляется произведение оценок R и Т. Пятый слой значений выходного нейрона сети состоит из А-нейронов, на входы которых поступают выходные значения RT-нейронов и связанные с ними достоверности правил CF. Каждый А-нейрон вычисляет комплексную оценку достоверности решения C и формирует на выходе максимальную из этих оценок. В шестом слое содержится один Pц-нейрон, формирующий значение выхода сети "pц=A", соответствующее А-нейрону с максимальной величиной оценки С. -нейроном связан параметр w, определяющий вес (важность) условия в правиле. Третий слой сети состоит из И-нейронов, определяющих оценку R степени срабатывания условной части правил. В четвертом слое сети вычисляется произведение оценок R и Т. Пятый слой значений выходного нейрона сети состоит из А-нейронов, на входы которых поступают выходные значения RT-нейронов и связанные с ними достоверности правил CF. Каждый А-нейрон вычисляет комплексную оценку достоверности решения C и формирует на выходе максимальную из этих оценок. В шестом слое содержится один Pц-нейрон, формирующий значение выхода сети "pц=A", соответствующее А-нейрону с максимальной величиной оценки С.
Для определения возможности и эффективности практического использования разработанной нейронечеткой модели потребовалась оценка ее аппроксимирующей способности. Данная оценка производилась на основе анализа следующих факторов:
- сходимости разработанного алгоритма обучения, используемого для построения нейронечеткой модели;
- удовлетворения работы ННС принципам нечеткой аппроксимации;
- непротиворечивости алгоритма логического вывода в ННС алгоритму аппроксимации объектов с дискретным выходом на основе нечеткой базы знаний.
Оценка аппроксимирующей способности нейронечеткой модели
Важным моментом всех алгоритмов обучения нейронных сетей является вопрос их сходимости. Сходимость разработанного алгоритма обучения ННС обусловлена следующими факторами:
- настройка параметров ФП в ННС производится на основе метода градиентного спуска – эффективного метода оптимизации [7];
- экспериментальной способностью к обучению нечеткой нейронной сети с одновременным уменьшением ошибки выхода.
Метод градиентного спуска основывается на известном факте, что градиент функции показывает направление ее наискорейшего возрастания, а антиградиент – направление убывания. При этом модуль градиента характеризует скорость этого процесса. Вектор градиента может быть получен через свои проекции на оси координат, которые равны частным производным по соответствующим аргументам целевой функции. Градиент перпендикулярен линии уровня, проходящей через ту точку, в которой он вычислен.
Многократное итерационное повторение данного метода в алгоритме обучения ННС позволяет определять оптимальные значения параметров ФП. При этом ошибка выхода сети стремится к своему минимальному значению.
Настройка значений параметров ФП в продукционных правилах с одновременным уменьшением ошибки выхода нечеткой нейронной сети приводит к повышению точности аппроксимации экспериментальных данных нечеткими гранулами, часто наделенными лингвистической интерпретацией. На принципе аппроксимации экспериментальных данных нечеткими гранулами базируются теоремы о нечеткой аппроксимации [26-30].
В общем случае задача нечеткой аппроксимации может быть рассмотрена, как аппроксимация непрерывной функции f : X -> Y в виде нечеткого объединения, называемого гранулированной спецификацией [16]:
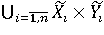 , (7) , (7)
где 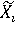 , , 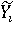 – нечеткие гранулы. – нечеткие гранулы.
Лингвистическая аппроксимация имеет место при наделении нечетких множеств 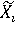 , , 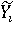 , , 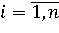 языковой интерпретацией. Данная аппроксимация может рассматриваться, как формализация функции f : X -> Y набором нечетких продукций, то есть нечеткой системой, функционирующей по этим правилам. языковой интерпретацией. Данная аппроксимация может рассматриваться, как формализация функции f : X -> Y набором нечетких продукций, то есть нечеткой системой, функционирующей по этим правилам.
Система F, определяемая совокупностью нечетко-продукционных правил, отображает нечеткое множество 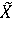 , поданное на ее вход, в нечеткое множество , поданное на ее вход, в нечеткое множество 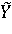 , являющееся ее выходом. Нечеткие гранулы ( , являющееся ее выходом. Нечеткие гранулы (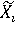 , , 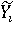 ), ), 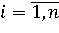 , соответствующие нечетким правилам, определяют покрытие функции f аппроксимирующими ее нечеткими отпечатками [28]. На рисунке 2 показан пример аппроксимации непрерывной функции нечеткими отпечатками. , соответствующие нечетким правилам, определяют покрытие функции f аппроксимирующими ее нечеткими отпечатками [28]. На рисунке 2 показан пример аппроксимации непрерывной функции нечеткими отпечатками.
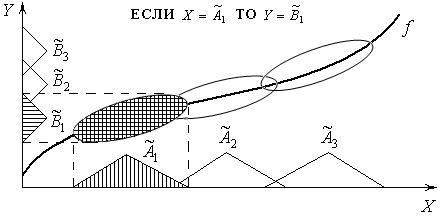
Рис. 2. Пример аппроксимации непрерывной функции нечеткими отпечатками
Для дискретной функции f аппроксимация ее нечеткими отпечатками будет иметь вид, как показано на рисунке 3.
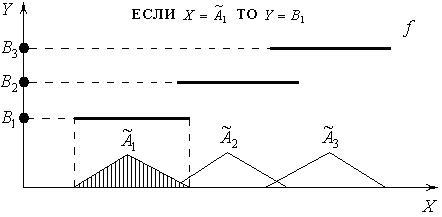
Рис. 3. Пример аппроксимации дискретной функции нечеткими отпечатками
Таким образом, используя нечеткие продукционные правила, лингвистическая аппроксимация позволяет выполнять приближение функции f. При необходимости более точной аппроксимации необходима более детальное гранулирование осей координат, то есть использование большего числа значений лингвистических переменных и, соответственно, большего количества нечетко-продукционных правил. Применительно к ННС это требование сводится к выбору количества градаций для входных лингвистических переменных.
Обученная ННС является аддитивной нечеткой системой, задаваемой совокупностью формируемых нечетко-продукционных правил. Каждое из них устанавливает некоторую область в пространстве решений с нечеткими размытыми границами, определяемыми коэффициентами достоверности правил CF и важности их нечетких градаций w. В совокупности правила производят аппроксимацию анализируемых данных нечеткими гранулами.
Для окончательной оценки аппроксимирующей способности разработанной нечеткой нейронной сети сопоставим используемый в ней алгоритм нечеткого логического вывода с алгоритмом А. П. Ротштейна [20], используемого для аппроксимации объектов с дискретным выходом. Для этого представим разработанный алгоритм вывода в матричном виде (см. рис. 4).
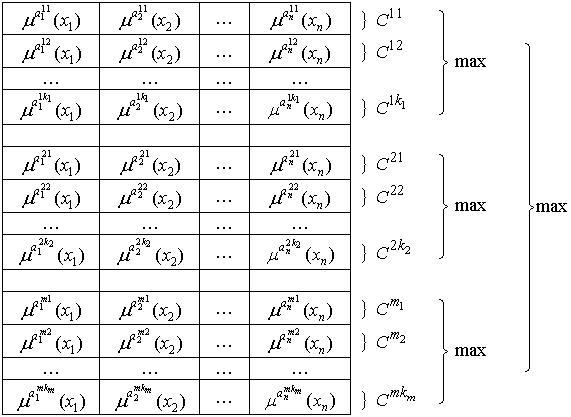
Рис. 4. Матричный вид алгоритма логического вывода
Здесь Cjp, 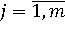 , , 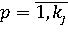 – комплексная оценка достоверности jp-го правила, равная произведению (R*T*CF)jp, где – комплексная оценка достоверности jp-го правила, равная произведению (R*T*CF)jp, где 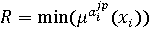 , , 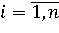 . Можно показать, что при T = 1 и CF = 1 разработанный алгоритм становится эквивалентным алгоритму А. П. Ротштейна. Следовательно, при данных ограничениях алгоритм логического вывода позволяет производить аппроксимацию объектов с дискретным выходом. В случае, когда параметры T и CF отличны от единицы, логика работы алгоритма не нарушается и его можно рассматривать, как обобщение алгоритма А. П. Ротштейна. При этом оценка T позволяет расширить применимость алгоритма на случай неполных входных данных, а коэффициент CF позволяет ранжировать предлагаемые решения. . Можно показать, что при T = 1 и CF = 1 разработанный алгоритм становится эквивалентным алгоритму А. П. Ротштейна. Следовательно, при данных ограничениях алгоритм логического вывода позволяет производить аппроксимацию объектов с дискретным выходом. В случае, когда параметры T и CF отличны от единицы, логика работы алгоритма не нарушается и его можно рассматривать, как обобщение алгоритма А. П. Ротштейна. При этом оценка T позволяет расширить применимость алгоритма на случай неполных входных данных, а коэффициент CF позволяет ранжировать предлагаемые решения.
Таким образом, опираясь на приведенные оценки аппроксимирующей способности разработанной нечеткой нейронной сети, можно сделать вывод, что нейронечеткая модель является эффективным аппроксиматором объектов с дискретным выходом.
Оценка классифицирующей способности формируемых нечетко-продукционных правил
В качестве апробации предложенного подхода к формированию нечетких правил на основе нейронечеткой модели проведена оценка их классифицирующей способности на базе разработанного программного комплекса [13]. Исследования проводились на примере решения известных задач классификации путем анализа данных из общедоступного источника UCI Machine Learning Repository [25].
В таблице 1 представлена информация о характеристиках наборов исходных данных, соответствующих решаемым задачам классификации.
Табл. 1. Характеристика исходных данных
|
Набор исходных данных
|
Число входных параметров
|
Типы входных параметров
|
Объем выборки
|
Число классов
|
|
Iris Plants Database
|
4
|
числовые
|
150
|
3
|
|
BUPA Liver Disorders
|
6
|
числовые
|
345
|
2
|
|
Australian Credit Approval
|
14
|
числовые, категориальные
|
690
|
2
|
|
German Credit Data
|
20
|
числовые, категориальные
|
1000
|
2
|
Первый набор данных соответствует задаче классификации видов ирисов Фишера. Во втором наборе представлены данные, соответствующие задаче диагностирования заболевания печени человека по результатам анализа его крови. Третий набор соответствует задаче выявления подозрительных транзакций с банковскими картами. Четвертый набор соответствует задаче принятия решения о выдаче потребительского кредита на основании анкетных данных заемщика.
Для оценки классифицирующей способности формируемых нечетких правил проведены исследования, основанные на выполнении этапов [9]:
1) построение систем нечетко-продукционных правил для нечеткой аппроксимации зависимостей в каждом наборе данных;
2) сравнение результатов классификации на основе сформированных систем правил с известными результатами других авторов.
На первом этапе были сформированы системы нечетких правил, соответствующие анализируемым наборам данных (см. табл. 2).
Табл. 2. Характеристики сформированных систем правил
|
Параметры БЗ
Набор данных
|
Число сформированных правил
|
Точность классификации
|
|
Iris Plants Database
|
44
|
0,98
|
|
BUPA Liver Disorders
|
87
|
0,762
|
|
Australian Credit Approval
|
537
|
0,859
|
|
German Credit Data
|
927
|
0,827
|
В качестве меры эффективности сформированных систем нечетких правил выступает точность классификации – отношение числа правильно классифицированных входных образов к общему числу анализируемых данных. Самая высокая точность классификации получена на наборе данных Iris Plants Database. На остальных выборках точность классификации ниже.
Для определения значимости полученных результатов классификации сравним их с известными результатами других авторов, проводивших исследования на тех же наборах данных. Так, в работах [3,22] проводились исследования эффективности различных методов классификации на трех наборах данных: BUPA Liver Disorders, Australian Credit Approval и German Credit Data. В таблице 3 приведено сравнение точности классификации, полученной при использовании сформированных систем нечетких правил, с точностью других методов классификации.
Табл. 3. Сравнение точности методов классификации
|
Наборы данных
Метод
классификации
|
BUPA Liver Disorders
|
Australian Credit Approval
|
German Credit Data
|
|
Коллективный классификатор на нечеткой логике
|
0,757
|
0,921
|
0,821
|
|
Классификатор на нечеткой логике
|
0,725
|
0,891
|
0,794
|
|
Байесовский классификатор
|
0,629
|
0,847
|
0,679
|
|
Многослойный персептрон
|
0,693
|
0,833
|
0,716
|
|
Бустинг
|
0,656
|
0,76
|
0,7
|
|
Бэггинг
|
0,63
|
0,847
|
0,684
|
|
Метод случайных подпространств
|
0,632
|
0,852
|
0,677
|
|
Коллектив нейронных сетей: простое усреднение
|
0,74
|
0,892
|
0,805
|
|
Коллектив нейронных сетей: равноправное голосование
|
0,783
|
0,918
|
0,815
|
|
Коллектив нейронных сетей: правило Борда
|
0,772
|
0,905
|
0,831
|
|
Коллектив нейронных сетей: многоярусное обобщение
|
0,785
|
0,925
|
0,852
|
|
Коллектив нейронных сетей: трехступенчатые эволюционные метод
|
0,804
|
0,947
|
0,857
|
|
Коэволюционный метод обучения алгоритмических композиций
|
0,644
|
0,866
|
0,746
|
|
Система нечетких правил
|
0,762
|
0,859
|
0,827
|
Из таблицы видно, что классифицирующая способность сформированных систем нечетких правил сравнима с точностью некоторых известных методов классификации (например, коллективом нейронных сетей, многослойным персептроном, классификатором на нечеткой логике), превосходит на 15% методы Байеса, Бустинга, Бэггинга, случайных подпространств и на 9% коэволюционный метод обучения алгоритмических композиций. Значимость полученных результатов на данном этапе исследований определяется возможностью использования сформированных систем нечетко-продукционных правил для решения задач классификации с точностью, не уступающей точности любых других известных методов классификации.
В работе [24] приведены результаты исследования эффективности метода нечеткой классификации на наборе данных Iris Plants Database. Данный метод был специально разработан автором для выполнения нечеткого логического вывода в среде MATLAB при аппроксимации объектов с дискретным выходом. Для полноты экспериментов на том же наборе данных построен нейросетевой классификатор (многослойный персептрон) на базе аналитической платформы Deductor [17], а также спроектирован нейронечеткий классификатор ANFIS инструментальными средствами среды моделирования MATLAB.
Точность классификации на основе использования сформированной БЗ на наборе данных Iris Plants Database составила 0,98. Данная точность, как и в предыдущем случае, сравнима с точностью нейросетевого метода классификации на основе многослойного персептрона (0,987). Во всех остальных случаях разработанный метод позволяет достичь лучшего результата классификации: на 3% превышает точность метода нечеткой классификации объектов с дискретным выходом (0,947) и на 1% – точность нейронечеткого метода на основе нечеткой нейронной сети ANFIS (0,973). Таким образом, преимущество использования предложенного метода классификации перед нечетким и нейронечетким методами заключается в повышении точности классификации, а, следовательно, в возможности принятия более точных решений в составе интеллектуальных систем оценки состояния объектов.
Следует отметить, что, несмотря на совпадение точности классификации предложенным и нейросетевым методами, в интеллектуальных системах оценки состояния объектов целесообразно использовать метод классификации на основе формирования базы нечетких правил, так как такие модели, в отличие от нейросетевых, поддаются лингвистической интерпретации. Таким образом, формируемые системы нечетко-продукционных правил совместно с разработанными алгоритмами логического вывода являются эффективными функциональными аппроксиматорами объектов с дискретным выходом и обладают высокой степенью классифицирующей способности.
Заключение
Описанная в данной работе нейронечеткая модель, основанная на обучении нечеткой нейронной сети, позволяет формировать систему нечетких правил, используемых для оценки состояния объектов. Эта задача является разновидностью задачи классификации. В данном случае нечеткий классификатор на основе формируемых нечетких правил производит аппроксимацию объектов с дискретным выходом. Несмотря на большое количество методов и алгоритмов классификации, используемых в настоящее время в интеллектуальных системах, разработанная модель обладает рядом преимуществ, главное из которых – высокая аппроксимирующая способность. Как показали результаты проведенных исследований, нейронечеткую модель можно считать эффективным аппроксиматором объектов с дискретным выходом. Это позволяет формировать системы нечетких правил на основе обучения сети на экспериментальных данных и успешно использовать их в механизмах поддержки принятия решений.
Практическая ценность предложенного подхода заключается в возможности построения эффективных систем поддержки принятия решений по оценке состояния объектов в различных предметных областях.
Библиография
1. Аникин И.В. Технология интеллектуального анализа данных для выявления внутренних нарушителей в компьютерных системах // Научно-технические ведомости Санкт-Петербургского государственного политехнического университета. Информатика. Телекоммуникации. Управление. – 2010. – № 6 (113). – С. 112-117.
2. Ахметвалеев А.М., Катасёв А.С. Нейросетевая модель и программный комплекс определения функционального состояния человека // Автоматизация процессов управления. 2017. № 3 (49). С. 88-95.
3. Бухтояров В.В. Трехступенчатый эволюционный метод формирования коллективов нейронных сетей для решения задач классификации // Программные продукты и системы. – 2012. – № 4. – С. 101-106.
4. Глова В.И., Катасёв А.С., Корнилов Г.С. Преднастройка и оптимизация параметров нечеткой нейронной сети при формировании баз знаний экспертных систем // Информационные технологии. – 2010. – № 5. – С. 15-19.
5. Горбунов Д.В., Нестерова С.И., Рамзаев В.М., Хаймович И.Н., Чумак В.Г. Управление инновационным процессом развития малого бизнеса в регионе на основе интеллектуального анализа данных (технология Big Data) // Фундаментальные исследования. 2016. № 4-2. С. 381-386.
6. Емалетдинова Л.Ю., Катасёв А.С., Кирпичников А.П. Нейронечеткая модель аппроксимации сложных объектов с дискретным выходом // Вестник Казанского технологического университета. – 2014. – Т. 17. № 1. – С. 295-299.
7. Кабанихин С.И., Гасанов А., Пененко А.В. Метод градиентного спуска для решения обратной коэффициентной задачи теплопроводности // Сибирский журнал вычислительной математики. – 2008. – Т. 11. № 1. – С. 41-54.
8. Катасёв А.С. Аппроксимация объектов с дискретным выходом на основе нечетко-продукционных баз знаний // Вестник Казанского государственного технического университета им. А.Н. Туполева. – 2013. – № 4. – С. 212-217.
9. Катасёв А.С. Математическое и программное обеспечение формирования баз знаний мягких экспертных систем диагностики состояния сложных объектов: монография. – Казань: ГБУ «Республиканский центр мониторинга качества образования», 2013. – 200 с.
10. Катасёв А.С., Ахатова Ч.Ф. Гибридная нейронечеткая модель интеллектуального анализа данных для формирования баз знаний мягких экспертных диагностических систем // Наука и образование: научное издание МГТУ им. Н.Э. Баумана. – 2012. – № 12. – С. 34-42.
11. Катасёв А.С., Емалетдинова Л.Ю. Нечетко-продукционная каскадная модель диагностики состояния сложного объекта // Программные системы и вычислительные методы. – 2013. – № 1. – С. 69-81.
12. Катасёв А.С., Катасёва Д.В., Кирпичников А.П. Распознавание рукописных символов на базе искусственной нейронной сети // Вестник технологического университета. – 2015. – Т. 18. № 11. – С. 173-176.
13. Катасёв А.С., Левадный Т.Р. Свидетельство о государственной регистрации программы для ЭВМ № 2013661597. Программа для автоматизированного формирования баз знаний мягких экспертных диагностических систем. – М.: Роспатент, 2013.
14. Кошкин О.В., Сидоркина И.Г. Интеллектуальные технологии создания и проектирования открытых образовательных систем // Известия ТРТУ. 2003. № 2 (31). С. 269-273.
15. Круглов В.В. Адаптивные системы нечеткого вывода // Нейрокомпьютеры: разработка и применение. – 2003. – № 5. – С. 15-19.
16. Круглов В.В. Сравнение алгоритмов Мамдани и Сугено в задаче аппроксимации функции // Нейрокомпьютеры: разработка, применение. – 2003. – № 5. – С. 70-82.
17. Паклин Н.Б., Орешков В.И. Бизнес-аналитика: от данных к знаниям: учебное пособие. – 2-е изд., испр. – СПб.: Питер, 2013. – 704 с.: ил.
18. Палюх Б.В., Большаков С.В. Оценка качества образования в вузе с помощью интеллектуальных технологий анализа данных // Вестник Тверского государственного технического университета. – 2007. – № 10. – С. 248-251.
19. Подлесных В.Г. Продукционная парадигма моделирования сложных объектов и систем // Новые информационные технологии в автоматизированных системах. – 2014. – № 17. – С. 105-114.
20. Ротштейн А.П. Интеллектуальные технологии идентификации: нечеткая логика, генетические алгоритмы, нейронные сети. – Винница: УНИВЕРСУМ-Винница, 1999. – 320 с.
21. Семенкина М.Е. Самоадаптивные эволюционные алгоритмы проектирования информационных технологий интеллектуального анализа данных // Искусственный интеллект и принятие решений. 2013. № 1. С. 13-24.
22. Сергиенко Р.Б. Метод формирования нечеткого классификатора самонастраивающимися коэволюционными алгоритмами // Искусственный интеллект и принятие решений. – 2010. – № 3. – С. 98-106.
23. Талипов Н.Г., Катасёв А.С. Система поддержки принятия решений по распределению заданий по ведению реестра операторов персональных данных на основе нечетко-продукционной модели // Кибернетика и программирование. 2016. № 6. С. 96-114.
24. Штовба С.Д. Классификация объектов на основе нечеткого логического вывода // Exponenta Pro-Математика в приложениях. – 2004. – № 1(5). – С. 68-69.
25. Bache K., Lichman M. UCI Machine Learning Repository. – URL: http://archive.ics.uci.edu/ml.
26. Castro J.L. Fuzzy logic controllers are universal approximators // IEEE Trans. on Systems, Man and Cyb. Part B: Cybernetics. – 1995. – Vol. 25. – P. 629-635.
27. Castro J.L., Delgado M. Fuzzy Systems With Defuzzification Are Universal Approximators // IEEE Transactions on Systems, Man and Cybernetics. – Part B: Cybernet. – 1996. – Vol. 26. – P. 149-152.
28. Kosko B. Fuzzy systems as universal approximators // IEEE Transactions on Computers. – 1994. – Vol. 43. N 11. – P. 1329-1333.
29. Wang L.X. Fuzzy systems are universal approximators // Proceedgins of IEEE International Conference on Fuzzy Systems. – San Diego, CA, 1992. – Vol. 10. – P. 1163-1170.
30. Wang L.X., Mendel J.M. Fuzzy basis functions, universal approximation, and orthogonal least squares learning // IEEE Transactions of Neural Networks. – 1992. – Vol. 3. – P. 807-813
References
1. Anikin I.V. Tekhnologiya intellektual'nogo analiza dannykh dlya vyyavleniya vnutrennikh narushitelei v komp'yuternykh sistemakh // Nauchno-tekhnicheskie vedomosti Sankt-Peterburgskogo gosudarstvennogo politekhnicheskogo universiteta. Informatika. Telekommunikatsii. Upravlenie. – 2010. – № 6 (113). – S. 112-117.
2. Akhmetvaleev A.M., Katasev A.S. Neirosetevaya model' i programmnyi kompleks opredeleniya funktsional'nogo sostoyaniya cheloveka // Avtomatizatsiya protsessov upravleniya. 2017. № 3 (49). S. 88-95.
3. Bukhtoyarov V.V. Trekhstupenchatyi evolyutsionnyi metod formirovaniya kollektivov neironnykh setei dlya resheniya zadach klassifikatsii // Programmnye produkty i sistemy. – 2012. – № 4. – S. 101-106.
4. Glova V.I., Katasev A.S., Kornilov G.S. Prednastroika i optimizatsiya parametrov nechetkoi neironnoi seti pri formirovanii baz znanii ekspertnykh sistem // Informatsionnye tekhnologii. – 2010. – № 5. – S. 15-19.
5. Gorbunov D.V., Nesterova S.I., Ramzaev V.M., Khaimovich I.N., Chumak V.G. Upravlenie innovatsionnym protsessom razvitiya malogo biznesa v regione na osnove intellektual'nogo analiza dannykh (tekhnologiya Big Data) // Fundamental'nye issledovaniya. 2016. № 4-2. S. 381-386.
6. Emaletdinova L.Yu., Katasev A.S., Kirpichnikov A.P. Neironechetkaya model' approksimatsii slozhnykh ob''ektov s diskretnym vykhodom // Vestnik Kazanskogo tekhnologicheskogo universiteta. – 2014. – T. 17. № 1. – S. 295-299.
7. Kabanikhin S.I., Gasanov A., Penenko A.V. Metod gradientnogo spuska dlya resheniya obratnoi koeffitsientnoi zadachi teploprovodnosti // Sibirskii zhurnal vychislitel'noi matematiki. – 2008. – T. 11. № 1. – S. 41-54.
8. Katasev A.S. Approksimatsiya ob''ektov s diskretnym vykhodom na osnove nechetko-produktsionnykh baz znanii // Vestnik Kazanskogo gosudarstvennogo tekhnicheskogo universiteta im. A.N. Tupoleva. – 2013. – № 4. – S. 212-217.
9. Katasev A.S. Matematicheskoe i programmnoe obespechenie formirovaniya baz znanii myagkikh ekspertnykh sistem diagnostiki sostoyaniya slozhnykh ob''ektov: monografiya. – Kazan': GBU «Respublikanskii tsentr monitoringa kachestva obrazovaniya», 2013. – 200 s.
10. Katasev A.S., Akhatova Ch.F. Gibridnaya neironechetkaya model' intellektual'nogo analiza dannykh dlya formirovaniya baz znanii myagkikh ekspertnykh diagnosticheskikh sistem // Nauka i obrazovanie: nauchnoe izdanie MGTU im. N.E. Baumana. – 2012. – № 12. – S. 34-42.
11. Katasev A.S., Emaletdinova L.Yu. Nechetko-produktsionnaya kaskadnaya model' diagnostiki sostoyaniya slozhnogo ob''ekta // Programmnye sistemy i vychislitel'nye metody. – 2013. – № 1. – S. 69-81.
12. Katasev A.S., Kataseva D.V., Kirpichnikov A.P. Raspoznavanie rukopisnykh simvolov na baze iskusstvennoi neironnoi seti // Vestnik tekhnologicheskogo universiteta. – 2015. – T. 18. № 11. – S. 173-176.
13. Katasev A.S., Levadnyi T.R. Svidetel'stvo o gosudarstvennoi registratsii programmy dlya EVM № 2013661597. Programma dlya avtomatizirovannogo formirovaniya baz znanii myagkikh ekspertnykh diagnosticheskikh sistem. – M.: Rospatent, 2013.
14. Koshkin O.V., Sidorkina I.G. Intellektual'nye tekhnologii sozdaniya i proektirovaniya otkrytykh obrazovatel'nykh sistem // Izvestiya TRTU. 2003. № 2 (31). S. 269-273.
15. Kruglov V.V. Adaptivnye sistemy nechetkogo vyvoda // Neirokomp'yutery: razrabotka i primenenie. – 2003. – № 5. – S. 15-19.
16. Kruglov V.V. Sravnenie algoritmov Mamdani i Sugeno v zadache approksimatsii funktsii // Neirokomp'yutery: razrabotka, primenenie. – 2003. – № 5. – S. 70-82.
17. Paklin N.B., Oreshkov V.I. Biznes-analitika: ot dannykh k znaniyam: uchebnoe posobie. – 2-e izd., ispr. – SPb.: Piter, 2013. – 704 s.: il.
18. Palyukh B.V., Bol'shakov S.V. Otsenka kachestva obrazovaniya v vuze s pomoshch'yu intellektual'nykh tekhnologii analiza dannykh // Vestnik Tverskogo gosudarstvennogo tekhnicheskogo universiteta. – 2007. – № 10. – S. 248-251.
19. Podlesnykh V.G. Produktsionnaya paradigma modelirovaniya slozhnykh ob''ektov i sistem // Novye informatsionnye tekhnologii v avtomatizirovannykh sistemakh. – 2014. – № 17. – S. 105-114.
20. Rotshtein A.P. Intellektual'nye tekhnologii identifikatsii: nechetkaya logika, geneticheskie algoritmy, neironnye seti. – Vinnitsa: UNIVERSUM-Vinnitsa, 1999. – 320 s.
21. Semenkina M.E. Samoadaptivnye evolyutsionnye algoritmy proektirovaniya informatsionnykh tekhnologii intellektual'nogo analiza dannykh // Iskusstvennyi intellekt i prinyatie reshenii. 2013. № 1. S. 13-24.
22. Sergienko R.B. Metod formirovaniya nechetkogo klassifikatora samonastraivayushchimisya koevolyutsionnymi algoritmami // Iskusstvennyi intellekt i prinyatie reshenii. – 2010. – № 3. – S. 98-106.
23. Talipov N.G., Katasev A.S. Sistema podderzhki prinyatiya reshenii po raspredeleniyu zadanii po vedeniyu reestra operatorov personal'nykh dannykh na osnove nechetko-produktsionnoi modeli // Kibernetika i programmirovanie. 2016. № 6. S. 96-114.
24. Shtovba S.D. Klassifikatsiya ob''ektov na osnove nechetkogo logicheskogo vyvoda // Exponenta Pro-Matematika v prilozheniyakh. – 2004. – № 1(5). – S. 68-69.
25. Bache K., Lichman M. UCI Machine Learning Repository. – URL: http://archive.ics.uci.edu/ml.
26. Castro J.L. Fuzzy logic controllers are universal approximators // IEEE Trans. on Systems, Man and Cyb. Part B: Cybernetics. – 1995. – Vol. 25. – P. 629-635.
27. Castro J.L., Delgado M. Fuzzy Systems With Defuzzification Are Universal Approximators // IEEE Transactions on Systems, Man and Cybernetics. – Part B: Cybernet. – 1996. – Vol. 26. – P. 149-152.
28. Kosko B. Fuzzy systems as universal approximators // IEEE Transactions on Computers. – 1994. – Vol. 43. N 11. – P. 1329-1333.
29. Wang L.X. Fuzzy systems are universal approximators // Proceedgins of IEEE International Conference on Fuzzy Systems. – San Diego, CA, 1992. – Vol. 10. – P. 1163-1170.
30. Wang L.X., Mendel J.M. Fuzzy basis functions, universal approximation, and orthogonal least squares learning // IEEE Transactions of Neural Networks. – 1992. – Vol. 3. – P. 807-813
Ссылка на эту статью
Просто выделите и скопируйте ссылку на эту статью в буфер обмена. Вы можете также
попробовать найти похожие
статьи
|
|





