|
ГЛАВНАЯ
> Вернуться к содержанию
Кибернетика и программирование
Правильная ссылка на статью:
Пономарев Д.Ю.
Оптимизационная модель спутниковой инфокоммуникационной сети
// Кибернетика и программирование.
2017. № 4.
С. 66-74.
DOI: 10.25136/2644-5522.2017.4.21176 URL: https://nbpublish.com/library_read_article.php?id=21176
Оптимизационная модель спутниковой инфокоммуникационной сети
Пономарев Дмитрий Юрьевич
кандидат технических наук
доцент, Сибирский государственный аэрокосмический университет им. академика М.Ф. Решетнева
660037, Россия, Красноярский край, г. Красноярск, пр. им. газеты Красноярский рабочий, 31
Ponomarev Dmitriy
PhD in Technical Science
Associate Professor, Department of Electrical Engineering and Telecommunications, Reshetnev Siberian State Aerospace University.
660037, Russia, Krasnoyarskii krai, g. Krasnoyarsk, pr. im. gazety Krasnoyarskii rabochii, 31

|
ponomarevdu@yandex.ru
|
|
 |
Другие публикации этого автора
|
|
|
DOI: 10.25136/2644-5522.2017.4.21176
Дата направления статьи в редакцию:
22-11-2016
Дата публикации:
17-09-2017
Аннотация:
В качестве объекта исследования в работе рассматриваются многоуровневые спутниковые инфокоммуникационные сети. Динамическое влияние факторов разного рода на характеристики линий связи на различных участках сети приводит к изменению распределения трафика в исследуемой сети, что в свою очередь может приводить к снижению показателей качества обслуживания, одним из которых является среднее время задержки доставки информации. В работе представлены результаты разработки модели оптимизации распределения трафика в спутниковой иерархической сети связи по критерию минимума среднего времени задержки с целью повышения качества обслуживания информационных потоков в исследуемой сети. Основным методом, используемым для разработки оптимизационной модели выбран узловой метод тензорного анализа сетей, удовлетворяющий, как по возможностям учета взаимодействия топологии сети и процессов обслуживания информационных потоков, так и по используемому набору исходных данных. Научная новизна заключается в использовании узлового метода тензорного анализа к задаче оптимизации распределения трафика в иерархической инфокоммуникационной спутниковой сети по критерию минимума среднего времени задержки путем использования целевой функции, учитывающей среднее время задержки в каждой системе маршрута передачи информации, и ограничений, определяемых тензорным уравнением поведения исходной сети.
Ключевые слова:
спутниковые сети, среднее время задержки, тензорный анализ сетей, узловой метод, качество обслуживания, иерархические сети, топология сети, межспутниковые линии связи, загрузка системы, метод множителей Лагранжа
Abstract: The researcdh object in this study involves the multi-level satellite infocommunication networks. The dynamic influence of various factors upon the characteristics of communication lines in different elements of the network causes changes in the distribution of traffic within the studied network, which in turn can lead to a decline in service quality markers, one of which is the average delay in the delivery of information. The article presents the results of the development of the traffic optimization model in the satellite hierarchical communication network based upon the criterion of minimum mean delay time for the purpose of improving the quality of information flows in the studied network. The key method used to develop the optimization model is the node method for the tensor analysis of networks, which fits the requirements of accounting for the interaction of the network topology and the processes of servicing information flows, and the used set of initial data. The scientific novelty involves the use of the nodal tensor analysis method in order to optimize the traffic distribution in the hierarchical infocommunication satellite network using the criterion of minimum mean delay time by using an objective function that takes into account the average delay time in each system of the information transmission route and the constraints determined by the tensor equation of behavior of the initial network .
Keywords: Lagrange multipliers method, system load, inter-satellite link, network topology, hierarchical networks, quality of service, node method, tensor analysis of networks, average delay, satellite networks
Введение.
В настоящее время с целью формирования глобального информационного пространства без ограничений, накладываемых на мобильность пользователей, широко используются возможности технологий спутниковых инфокоммуникационных сетей. Современные и перспективные спутниковые технологии предполагают реализацию практически любого вида взаимодействия сетей и систем, включая мультисервисное обслуживание, путем применения различных алгоритмов обработки и передачи информации и разнообразных видов доступа [1-4].
Для решения задач специального назначения, например при обработке и передаче информации об оперативной обстановке на театре военных действий, требуется обеспечить своевременную (или в режиме реального времени) доставку сообщений в независимости от местонахождения объектов связи или наблюдения. Обеспечить такую возможность позволяют спутниковые инфокоммуникационные сети специального назначения. Построение таких сетей обычно основано на многоуровневом взаимодействии систем связи [5-7]. При этом, для обеспечения режима реального времени, необходимо обеспечить требуемое качество обслуживания трафика, одним из показателей которого является среднее время задержки [3,4,7-9].
Многоуровневое взаимодействие, используемое в иерархических спутниковых сетях, основано на декомпозиции функций, обеспечивающих обработку и передачу информации. Это позволяет: упростить алгоритмы взаимодействия систем, повысить надежность оборудования, обеспечить заданное качество обслуживания [5,7-9]. В многоуровневой иерархической спутниковой сети условно можно определить несколько уровней взаимодействия систем: спутниковые системы сбора информации (обычно низкие и средние орбиты ), спутниковые системы агрегации информации (возможно использование геостационарных систем), наземные системы обработки (анализа) информации [1-3,5,8,9]. Взаимодействие между уровнями сети и систем одного уровня обеспечивается спутниковыми линиями (в том числе и межспутниковыми) различного вида и их количество может динамически изменяться в зависимости от пространственного расположения спутниковых систем и других факторов [1-5,8-10]. Создаваемая отдельными системами сети задержка определяется интенсивностью нагрузки, поступающей на эти системы со стороны других систем.
Таким образом, для обеспечения своевременной и оперативной доставки информации с уровня сбора на уровень анализа необходимо обеспечить такое распределение трафика, которое бы приводило к минимизации среднего времени задержки информации в исследуемой спутниковой сети. Следовательно, актуальной является задача разработки модели оптимизации многоуровневой иерархической спутниковой инфокоммуникационной сети [6-9] по критерию минимизации среднего времени задержки.
Модель оптимизации спутниковой инфокоммуникационной сети.
Для иерархической трехуровневой (уровень сбора, уровень агрегации, уровень обработки) спутниковой инфокоммуникационной сети можно определить следующие множества моделей систем сети. Множество 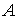 состоит из систем, моделирующих процессы сбора информации состоит из систем, моделирующих процессы сбора информации 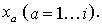 Множество Множество 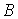 определяет модели систем уровня агрегации определяет модели систем уровня агрегации 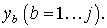 Множество Множество 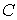 определяет модели систем уровня обработки определяет модели систем уровня обработки 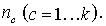 Задача состоит в определении загрузок (отношение интенсивности поступающего потока к интенсивности обслуживания) систем, моделирующих процессы обработки/передачи информации в спутниковой сети Задача состоит в определении загрузок (отношение интенсивности поступающего потока к интенсивности обслуживания) систем, моделирующих процессы обработки/передачи информации в спутниковой сети 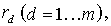 таких, что позволят обеспечить минимальное время задержки в исследуемой сети. таких, что позволят обеспечить минимальное время задержки в исследуемой сети.
Целевую функцию для такой оптимизационной задачи можно задать в виде суммы средних времен задержек для всех систем сети. Например, при использовании в качестве моделей систем массового обслуживания вида M/M/1, целевая функция записывается, как: 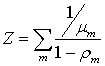 , где , где 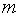 – номер системы модели, участвующие в процессах передачи и обработки информации в исследуемой спутниковой инфокоммуникационной сети; – номер системы модели, участвующие в процессах передачи и обработки информации в исследуемой спутниковой инфокоммуникационной сети; 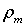 – загрузка m-ой системы модели (определяется интенсивностью нагрузки, поступающей в систему); – загрузка m-ой системы модели (определяется интенсивностью нагрузки, поступающей в систему); 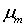 – интенсивность обслуживания обработки/передачи информации в системе – интенсивность обслуживания обработки/передачи информации в системе 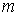 . Уравнение поведения узловой модели тензорного анализа сетей имеет следующий вид [10,11]: . Уравнение поведения узловой модели тензорного анализа сетей имеет следующий вид [10,11]:
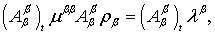 (1) (1)
где 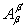 – тензор преобразования загрузок исходной (вспомогательной) и примитивной сетей [10,11], – тензор преобразования загрузок исходной (вспомогательной) и примитивной сетей [10,11], 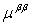 – тензор интенсивностей обслуживания, – тензор интенсивностей обслуживания, 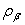 – тензор загрузок систем вспомогательной сети, – тензор загрузок систем вспомогательной сети, 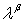 – тензор интенсивностей поступления. В данной работе в качестве вспомогательной сети рассматривается сеть массового обслуживания, обеспечивающая геометрические преобразования между исходной и примитивной сетями с целью введения информации о структуре связей между системами в модель исследуемой спутниковой сети [10,11]. – тензор интенсивностей поступления. В данной работе в качестве вспомогательной сети рассматривается сеть массового обслуживания, обеспечивающая геометрические преобразования между исходной и примитивной сетями с целью введения информации о структуре связей между системами в модель исследуемой спутниковой сети [10,11].
В соответствии с выводами, представленными в работе [11], уравнение (1) позволяет задать ограничения, накладываемые на целевую функцию минимизации среднего времени задержки для узловой модели спутниковой инфокоммуникационной сети . В таком случае система ограничений может быть определена, как:
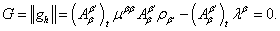 (2) (2)
Число уравнений 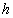 равно количеству узлов модели сети и обычно совпадает с числом систем модели [10]. Кроме использования системы (2) требуется обеспечить учет наличия мнимых систем [10,11] и выполнение условия равенства суммы потоков в узле модели нулю. равно количеству узлов модели сети и обычно совпадает с числом систем модели [10]. Кроме использования системы (2) требуется обеспечить учет наличия мнимых систем [10,11] и выполнение условия равенства суммы потоков в узле модели нулю.
Для обеспечения минимума среднего времени задержки сообщений в исследуемой спутниковой сети и в связи с тем, что целевая функция является нелинейной, при решении поставленной задачи используем метод множителей Лагранжа [11,12]. Функция Лагранжа для данного случая приобретает вид: 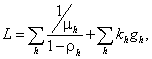 где: где: 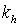 – множители Лагранжа, – множители Лагранжа, 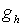 – уравнения системы ограничений (2). Таким образом, задача минимизации средней задержки в исследуемой спутниковой сети сводится к решению системы алгебраических уравнений, составленной из частных производных функции Лагранжа по всем переменным: – уравнения системы ограничений (2). Таким образом, задача минимизации средней задержки в исследуемой спутниковой сети сводится к решению системы алгебраических уравнений, составленной из частных производных функции Лагранжа по всем переменным: 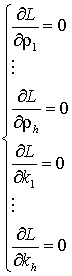 . .
В результате решения данной системы уравнений будут получены значения загрузок вспомогательной сети (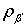 ), из которых определяются загрузки систем в исходной сети ( ), из которых определяются загрузки систем в исходной сети (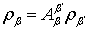 [10,11]), используя которые находим среднее время задержки ( [10,11]), используя которые находим среднее время задержки (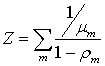 ) в исследуемой спутниковой сети. ) в исследуемой спутниковой сети.
Численные результаты.
В качестве примера использования предложенной модели оптимизации, рассмотрим спутниковую инфокоммуникационную сеть, структура которой представлена на рис. 1 и имеет три уровня.
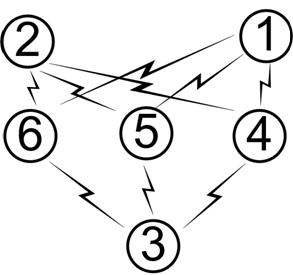
Рисунок 1. Обобщенная структура спутниковой сети
На первом уровне размещаются системы сбора (системы 1 и 2) на низких орбитах, ко второму уровню относятся системы агрегации (системы 4, 5, 6) на геостационарных или средних орбитах, на третьем наземном уровне производится обработка и анализ информации (система 3).
Как было отмечено ранее, в качестве модели спутниковой инфокоммуникационной сети рассматривается узловая модель тензорного анализа сетей [10]. Структура этой модели представлена на рис. 2.
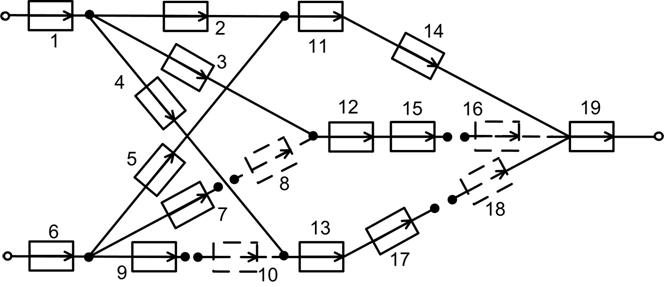
Рисунок 2. Структура узловой модели исследуемой сети
Спутниковая система 1 (рис. 1) моделируется системами 1-4 (рис. 2), где через систему 1 поток информации поступает в сеть и через системы 2, 3 и 4 поступает на модели спутниковых систем 4, 5 и 6 (т.е. на системы модели 11, 12 и 13) соответственно. Определенное ранее множество 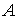 состоит из систем с 1 по 10, включая мнимые 8 и 10; множество состоит из систем с 1 по 10, включая мнимые 8 и 10; множество 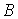 определяет модели систем уровня агрегации с 11 по 18, в том числе мнимые 16 и 18; множество определяет модели систем уровня агрегации с 11 по 18, в том числе мнимые 16 и 18; множество 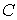 состоит из системы 19. состоит из системы 19.
Нагрузка, поступающая со спутниковых низкоорбитальных систем сбора поступает через системы модели 1 и 6, поэтому интенсивности трафика 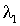 и и 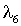 являются исходными данными. В связи с тем, что рассматриваются системы без потерь, должно соблюдаться условие равенства суммы интенсивностей на входе (интенсивности являются исходными данными. В связи с тем, что рассматриваются системы без потерь, должно соблюдаться условие равенства суммы интенсивностей на входе (интенсивности 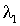 и и 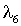 ) и выходе ) и выходе 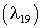 сети. Таким образом, целевая функция для данного частного случая записывается, как (при этом результат вносимый мнимыми системами не учитывается): сети. Таким образом, целевая функция для данного частного случая записывается, как (при этом результат вносимый мнимыми системами не учитывается): 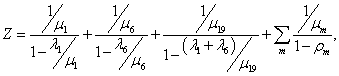 где где 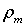 определяются тензором определяются тензором 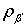 [10]. Интенсивности обслуживания определяются уровнем размещения системы в модели сети. [10]. Интенсивности обслуживания определяются уровнем размещения системы в модели сети.
Как было отмечено ранее, в качестве ограничений выступает матричное уравнение (2), полученное на основе (1). С учетом присутствия мнимых систем и необходимости выполнения условия равенства суммы интенсивностей потоков в узле нулю, систему ограничений записывается, как [10,11]:
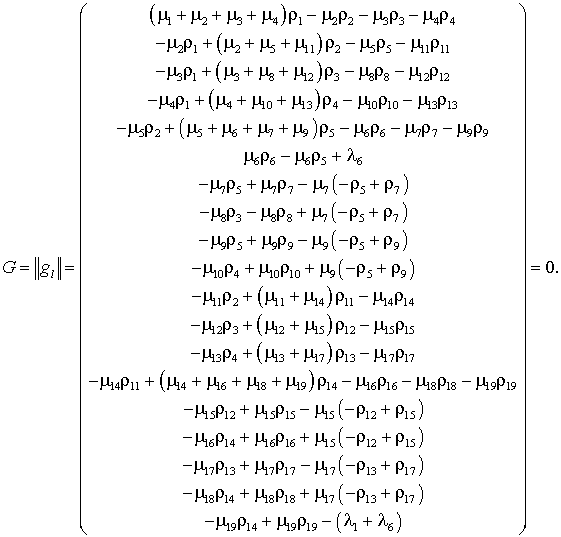 (3) (3)
Далее, необходимо сформировать функцию Лагранжа и систему уравнений, состоящую из частных производных этой функции по всем переменным. В результате решения системы уравнений для рассматриваемой спутниковой сети при заданных интенсивностях источников 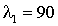 и и 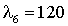 были получены значения загрузок, позволяющие обеспечить минимальное время задержки путем перераспределения трафика (табл. 1: все значения в условных единицах). были получены значения загрузок, позволяющие обеспечить минимальное время задержки путем перераспределения трафика (табл. 1: все значения в условных единицах).
Таблица 1. Результаты оптимизации распределения трафика в спутниковой сети
|
Номер системы модели
|
Интенсивности обслуживания 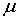
|
Интенсивности поступления 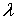
|
Загрузки систем 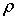
|
|
1
|
120
|
90
|
0.75
|
|
2
|
40
|
21.183
|
0.53
|
|
3
|
50
|
30.379
|
0.608
|
|
4
|
60
|
38.438
|
0.641
|
|
5
|
60
|
33.892
|
0.565
|
|
6
|
140
|
120
|
0.857
|
|
7,8
|
70
|
41.605
|
0.594
|
|
9,10
|
80
|
44.503
|
0.556
|
|
11
|
75
|
55.075
|
0.734
|
|
12
|
90
|
71.984
|
0.8
|
|
13
|
100
|
82.941
|
0.829
|
|
14
|
80
|
55.075
|
0.688
|
|
15,16
|
100
|
71.984
|
0.72
|
|
17,18
|
110
|
82.941
|
0.754
|
|
19
|
220
|
210
|
0.955
|
Среднее время задержки для найденного оптимального распределения интенсивностей поступления составило значение: 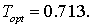 При равномерном распределении трафика, т.е. интенсивность При равномерном распределении трафика, т.е. интенсивность 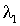 равномерно распределяется между системами модели 2, 3 и 4, а интенсивность равномерно распределяется между системами модели 2, 3 и 4, а интенсивность 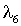 между системами модели 5, 7 и 9. В таком случае среднее время задержки в сети составляет 0.917, что относительно между системами модели 5, 7 и 9. В таком случае среднее время задержки в сети составляет 0.917, что относительно 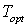 обеспечивает худшие показатели примерно на 30%. обеспечивает худшие показатели примерно на 30%.
Заключение.
Современные инфокоммуникационные спутниковые сети, в том числе и специального назначения, обладают сложной многоуровневой структурой и динамически изменяющейся, в основном в связи с непостоянством пространственного расположения систем, топологией. Для оперативной доставки информации спутниковая инфокоммуникационная сеть должна обеспечить минимальную задержку при обслуживании информационных потоков. Таким образом, требуется реализовать такое распределение трафика в исследуемой сети, которое бы привело к минимизации среднего времени задержки. Предложенная в данной работе модель оптимизации распределения трафика по критерию среднего времени задержки основана на тензорной методологии сетей и позволяет решать задачи обеспечения минимальной задержки в спутниковой инфокоммуникационной сети с учетом структурно-процессного взаимодействия.
Библиография
1. Maini A.K., Agrawal V. Satellite Technology: Principles and Applications. John Wiley & Sons Inc. 2014. 846 pp.
2. Minoli D. Innovations in satellite communication and satellite technology: the industry implications of DVB-S2X, high throughput satellites, Ultra HD, M2M, and IP. John Wiley & Sons Inc. 2015. 421 pp.
3. Kolawole M.O. Satellite Communication Engineering. CRC Press Taylor & Francis Group. 2014. 285 pp.
4. Тарасов С.С. Современные технологии и системы спутникового доступа в сеть интернет // T-Comm. 2013. № 10. С. 89-91.
5. Аганесов А.В. Модель сети спутниковой связи на основе протокола случайного множественного доступа S-ALOHA // Системы управления, связи и безопасности. 2015. № 2. С. 99-134.
6. Косяков Е.Н., Косаревич Д.В., Викторов Е.А. Моделирование процесса обслуживания неоднородного трафика в мультисервисных сетях спутниковой связи // Труды Военно-космической академии им. А.Ф. Можайского. 2011. № 632. С. 13-18.
7. Илюхин А.А., Щербаков М.В. Структурные и динамические свойства многоуровневого иерархического управления процессами обработки и передачи пакетных данных в мультисервисных спутниковых сетях // T-Comm. 2014. № 5. С. 28-32.
8. Nishiyama H., Tada Y., Kato N., Yoshimura N., Toyoshima M., Toward Optimized Traffic Distribution for Efficient Network Capacity Utilization in Two-Layered Satellite Networks // IEEE Transactions on Vehicular Technology. 2012. vol. 62. № 3. pp. 1303-1313.
9. Kawamoto Y., Nishiyama H., Kato N., Kadowaki N. A Traffic Distribution Technique to Minimize Packet Delivery Delay in Multilayered Satellite Networks // IEEE Transactions on Vehicular Technology. 2013. vol. 62. № 7. pp. 3315-3324.
10. Пономарев Д.Ю. Узловая модель распределения трафика для перспективных спутниковых сетей связи // Успехи современной радиоэлектроники. 2015. № 10. С. 55-58.
11. Пономарев Д.Ю. Оптимизация среднего времени задержки в сети IMS // Пятая Международная конференция «Системный анализ и информационные технологии» САИТ – 2013: Труды конференции. Красноярск: ИВМ СО РАН, 2013. Т. 2. С. 388-394
12. Гришенцев А.Ю., Коробейников А.Г. Постановка задачи оптимизации распределённых вычислительных систем // Программные системы и вычислительные методы. 2013. № 4. C. 370-375. DOI: 10.7256/2305-6061.2013.4.10548.
References
1. Maini A.K., Agrawal V. Satellite Technology: Principles and Applications. John Wiley & Sons Inc. 2014. 846 pp.
2. Minoli D. Innovations in satellite communication and satellite technology: the industry implications of DVB-S2X, high throughput satellites, Ultra HD, M2M, and IP. John Wiley & Sons Inc. 2015. 421 pp.
3. Kolawole M.O. Satellite Communication Engineering. CRC Press Taylor & Francis Group. 2014. 285 pp.
4. Tarasov S.S. Sovremennye tekhnologii i sistemy sputnikovogo dostupa v set' internet // T-Comm. 2013. № 10. S. 89-91.
5. Aganesov A.V. Model' seti sputnikovoi svyazi na osnove protokola sluchainogo mnozhestvennogo dostupa S-ALOHA // Sistemy upravleniya, svyazi i bezopasnosti. 2015. № 2. S. 99-134.
6. Kosyakov E.N., Kosarevich D.V., Viktorov E.A. Modelirovanie protsessa obsluzhivaniya neodnorodnogo trafika v mul'tiservisnykh setyakh sputnikovoi svyazi // Trudy Voenno-kosmicheskoi akademii im. A.F. Mozhaiskogo. 2011. № 632. S. 13-18.
7. Ilyukhin A.A., Shcherbakov M.V. Strukturnye i dinamicheskie svoistva mnogourovnevogo ierarkhicheskogo upravleniya protsessami obrabotki i peredachi paketnykh dannykh v mul'tiservisnykh sputnikovykh setyakh // T-Comm. 2014. № 5. S. 28-32.
8. Nishiyama H., Tada Y., Kato N., Yoshimura N., Toyoshima M., Toward Optimized Traffic Distribution for Efficient Network Capacity Utilization in Two-Layered Satellite Networks // IEEE Transactions on Vehicular Technology. 2012. vol. 62. № 3. pp. 1303-1313.
9. Kawamoto Y., Nishiyama H., Kato N., Kadowaki N. A Traffic Distribution Technique to Minimize Packet Delivery Delay in Multilayered Satellite Networks // IEEE Transactions on Vehicular Technology. 2013. vol. 62. № 7. pp. 3315-3324.
10. Ponomarev D.Yu. Uzlovaya model' raspredeleniya trafika dlya perspektivnykh sputnikovykh setei svyazi // Uspekhi sovremennoi radioelektroniki. 2015. № 10. S. 55-58.
11. Ponomarev D.Yu. Optimizatsiya srednego vremeni zaderzhki v seti IMS // Pyataya Mezhdunarodnaya konferentsiya «Sistemnyi analiz i informatsionnye tekhnologii» SAIT – 2013: Trudy konferentsii. Krasnoyarsk: IVM SO RAN, 2013. T. 2. S. 388-394
12. Grishentsev A.Yu., Korobeinikov A.G. Postanovka zadachi optimizatsii raspredelennykh vychislitel'nykh sistem // Programmnye sistemy i vychislitel'nye metody. 2013. № 4. C. 370-375. DOI: 10.7256/2305-6061.2013.4.10548.
Ссылка на эту статью
Просто выделите и скопируйте ссылку на эту статью в буфер обмена. Вы можете также
попробовать найти похожие
статьи
|
|





