|
DOI: 10.7256/2306-4196.2016.5.20414
Дата направления статьи в редакцию:
16-09-2016
Дата публикации:
29-01-2017
Аннотация:
В статье предложен подход к прогнозированию групп временных рядов с применением технологий кластерного анализа и принципов многоцелевой оптимизации. Разработано описание временных рядов – центроидов кластеров с использованием моделей прогнозирования на основе строго бинарных деревьев и многоцелевого модифицированного алгоритма клонального отбора, при реализации которого в процесс отбора лучших моделей прогнозирования вовлечены два показателя качества моделей: показатель аффинитета, основанный на расчете средней относительной ошибки прогнозирования, и показатель несовпадения тенденций. Учет двух показателей качества модели прогнозирования реализован с использованием принципов Парето-доминирования, применяемых при формировании новых популяций моделей прогнозирования в многоцелевом модифицированном алгоритме клонального отбора.В рамках решения задачи многоцелевой оптимизации при формировании новой популяции моделей прогнозирования для поддержания ее высокого разнообразия предложено учитывать значения расстояния скученности моделей прогнозирования. Показана перспективность применения общих моделей прогнозирования, формируемых на основе строго бинарных деревьев,для прогнозирования временных рядов, входящих в один кластер. Приведены результаты экспериментальных исследований, подтверждающие эффективность предложенного подхода к краткосрочному и среднесрочному прогнозированию групп временных рядов в рамках решения задачи многоцелевой оптимизации.
Ключевые слова:
временной ряд, модель прогнозирования, строго бинарное дерево, алгоритм клонального отбора, многоцелевая оптимизация, показатель аффинитета, показатель несовпадения тенденций, средняя относительная ошибка, Парето-доминирование, расстояние скученности
УДК: 004.8
Работа поддержана грантом РФФИ, номер 16-08-00771, тема «Интеллектуальные программно-математические средства индивидуального и группового прогнозирования временных рядов».
Abstract: In article the approach to forecasting of time series groups with use of technologies of the cluster analysis and the principles of multiobjective optimization has been offered. The description of time series – centroids of clusters with use of the forecasting models on the base of the strictly binary trees and the multiobjective modified clonal selection algorithm in case of which the implementation of two quality indicators of models – the affinity indicator based on calculation of an average forecasting relative error and the tendencies discrepancy indicator are involved in selection process of the best forecasting models has been developed. Accounting of quality two indicators of the forecasting model is realized with use of the Pareto-dominance principles applied when forming new populations of the forecasting models in the multiobjective modified clonal selection algorithm. Within the solution of a problem of multiobjective optimization when forming new population of the forecasting models for maintenance of its high variety it is offered to consider values of the crowding distance of the forecasting models. Prospects of application of the general forecasting models created on the base of the strictly binary trees for forecasting of the time series entering one cluster are shown. The results of experimental studies confirming the efficiency of the offered approach to short-term and mid-term forecasting of time series groups within the solution of a problem of multiobjective optimization are given.
Keywords: time series, forecasting model, strictly binary tree, clonal selection algorithm, multiobjective optimization, affinity indicator, tendencies discrepancy indicator, average error rate, Pareto-dominance, crowding distance
Введение В настоящее время во многих отраслях экономической и социальной сферы приходится решать задачи прогнозирования поведения различных сложно развивающихся процессов, представляемых с помощью временных рядов (ВР) [1 – 6]. При этом усложнение прогнозируемых процессов заставляет аналитиков учитывать при решении этих задач сразу несколько показателей качества (ПК) моделей прогнозирования (МП). Риски использования некорректных прогнозов возрастают с увеличением конкурентоспособности рынка, с включением в управляемые процессы большего числа населения. Использование, например, только средней относительной ошибки прогнозирования как единственного показателя качества построенной МП становится недостаточным в силу часто неподконтрольных изменений в экономике, производстве и общественных институтах.
Очевидно, что система принятия решений должна получать более качественную, оперативную и доступную информацию об изменениях и тенденциях в тех процессах, которыми она управляет. Следовательно, прогнозы из приближенных должны становится точными, учитывающими не только сегодняшнюю ситуацию, но также предпосылки будущих изменений. Сегодняшнее верное решение завтра с изменением ситуации может стать главной ошибкой менеджмента. Задача аналитика – предвидеть эти изменения и выполнить прогноз с учетом всех ключевых факторов.
При этом должно быть увеличено не только число ПК МП, но также должна быть обеспечена и более тщательная детализация прогнозов. В последние годы с повышением вычислительной способности современных информационных систем осуществляется переход от получения агрегированных результатов прогнозирования ключевых экономических и демографических факторов, которые могут показать лишь общее направление развитие анализируемой системы, к детализации результатов прогнозирования, которые позволяют выявить скрытые проблемы, а также предупредить негативные тенденции, влияние которых замедляет развитие.
Помощь в решении обозначенных проблем на сегодняшний момент уверенно предоставляют информационные технологии, в частности технологии «добычи знаний» (Data Mining) и искусственного интеллекта [7, 8]. Их развитие началось еще в прошлом веке и стремительно продолжается по сегодняшний день, обеспечивая аналитиков все более эффективными инструментами решения ключевых задач обработки данных.
Целью настоящей статьи является разработка метода прогнозирования групп ВР с использованием современных интеллектуальных технологий анализа данных и принципов многоцелевой оптимизации. Общая характеристика проблематики работы Ключевым моментом при решении задачи прогнозирования является выбор лучшей МП. В настоящее время выбор лучшей МП чаще всего осуществляется с использованием только одного ПК МП, основанного на вычислении средней относительной ошибки прогнозирования, – показателя аффинитета.
Использование данного показателя качества является очевидным и обоснованным в силу того, что он позволяет среди нескольких МП выбрать модель с минимальным расхождением между фактическим и прогнозным значениями анализируемого ВР, что, в сущности, и является задачей прогнозирования. Однако, весьма вероятна ситуация, когда учет только значения средней относительной ошибки прогнозирования может привести к неправильному выбору лучшей МП. Например, из рисунка 1, полученного по результатам прогнозирования с помощью модели краткосрочного прогнозирования (на 1 – 3 шага вперед), видно, что с увеличением горизонта прогнозирования (то есть при среднесрочном прогнозировании) данная МП показывает противоположное направление изменения тенденций ВР, что ведет к кратному увеличению ошибок прогнозирования.
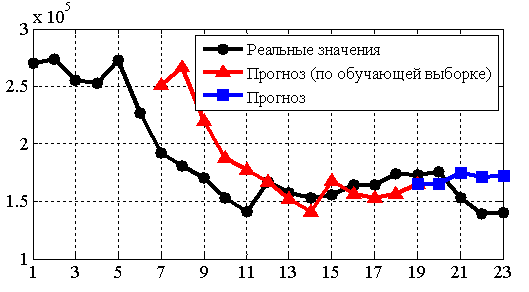
Рис. 1. Пример прогнозирования значений элементов временного ряда
Подобные ситуации заставляют искать альтернативные способы оценки качества МП, учитывающие, прежде всего, математический закон изменения прогнозируемой величины.
Вместе с тем, замена одного ПК МП на другой не допустима в силу того, что ни один из них не удовлетворяет всем предъявляемым требованиям. В связи с этим возникает проблема разработки алгоритмов одновременного учета нескольких ПК МП.
В сфере искусственного интеллекта для решения данной проблемы применяются технологии многоцелевой оптимизации, в рамках которых активно развиваются алгоритмы, основанные на соответствующих модификациях генетических алгоритмов (ГА) и алгоритмов клонального отбора (АКО).
Необходимо помнить, что учет нескольких ПК МП требует дополнительных вычислительных затрат. Усложняя алгоритм обработки, следует иметь в виду, что на сегодняшний день объемы наборов данных, над которыми необходимо производить сложные вычисления постоянно растут. К там наборам данных относятся и разнообразные группы ВР, для каждого из которых должен быть получен прогноз, то есть каждому ВР должна быть поставлена в соответствие некоторая МП. В связи с этим возникает необходимость в экономии вычислительной емкости на построение и актуализацию МП.
Для решения данной проблемы также возможно использование технологий искусственного интеллекта, а именно технологий кластерного анализа. Кластеризация – как инструментарий образования меньших наборов данных без задания первоначальных параметров классификации – позволяет обрабатывать однородные данные как один объект. Следовательно, в контексте задачи выбора МП можно построить общую МП (т.е. сформулировать математический закон) для группы ВР (а именно – для ВР-центроида кластера) и использовать эту модель для формирования индивидуальных прогнозов по каждому ВР.
Для разработки МП ВР-центроидов кластеров предлагается использовать подход, основанный на применении строго бинарных деревьев (СБД) и модифицированного алгоритма клонального отбора (МАКО) [9 – 15]. В этом случае удается сформировать аналитические зависимости, наилучшим образом описывающие известные значения ВР и обеспечивающие получение минимальных значений показателя аффинитета.
Далее в статье приведено теоретическое обоснование и экспериментальное подтверждение предложенных подходов к решению задачи прогнозирования групп ВР с использованием принципов многоцелевой оптимизации. Теоретическое обоснование предлагаемого метода прогнозирования Пусть имеется группа ВР `T`: `t_(i)` ` (i=1,m)`. Предположим, что каждый ВР `t_(i)` содержит `n` ` (10<=n<=30)` элементов `t_i^(j)" " (j=1,n)`, измеренных с некоторым постоянным шагом по времени.
МАКО, основанный на моделировании законов функционирования естественной иммунной системы, обеспечивает при разработке МП ВР на основе СБД формирование сложных аналитических зависимостей [9 – 12]. В [10] приведено подробное описание МАКО, реализующего построение и отбор МП на основе СБД. В МАКО в простейшем виде реализованы принципы распознавания антигенов с помощью антител. При этом для представления антигена Ag` ` используются известные значения элементов прогнозируемого ВР, а в роли антитела Ab выступает некоторая аналитическая зависимость, определяющая МП. В качестве «лучшего» антитела Ab выбирается антитело, обеспечивающее минимальное значение показателя аффинитета Aff [9 – 11].
Кодирование антитела Ab осуществляется посредством записи в строку символов, выбираемых из трёх символьных алфавитов [9 – 11]: алфавита арифметических операций (операций сложения, вычитания, умножения и деления) – Operation={'+', '–', '`.`', '/'}; алфавита функционалов Functional={'S', 'C', 'Q', 'L', 'E', '_'}, в котором символы 'S', 'C', 'Q', 'L', 'E' определяют математические функции «синус», «косинус», «квадратный корень», «натуральный логарифм», «экспонента», а символ '_' – отсутствие математической функции; алфавита терминалов Terminal={'a', 'b', 'c', ..., 'z', '?'}, в котором символы'a', 'b', 'c', ..., 'z' определяют аргументы аналитической зависимости, а символ '?' – константу. При использовании указанных выше трёх символьных алфавитов удается обеспечить корректное преобразование случайным образом формируемых антител, структура которых может быть описана с помощью СБД, в аналитические зависимости [9 – 11].
Для обеспечения высокой точности прогнозирования ВР со сложно формализуемым математическим законом при формировании антител используются СБД со структурой аналогичной той, что приведена на рисунке 2. Искомое СБД получается в результате композиции одного «левого» поддерева максимально возможного порядка `K=3` и некоторого количества «правых» поддеревьев максимально возможного порядка `K=2`. При этом термины «левое» и «правое» поддерево используются для указания того, в какую ветвь (левую или в правую) некоторого уровня СБД следует включать новое поддерево [10].
При формировании антитела целесообразно сначала реализовать разбиение СБД на поддеревья. Далее выполнить обход вершин каждого поддерева с формированием упорядоченных списков символов, находящихся в его вершинах. Затем – последовательное объединение этих списков [9 – 11]. При формировании упорядоченного списка символов на основе поддерева осуществляется последовательный двукратный обход его вершин. При этом сначала при движении по поддереву «снизу-вверх» и «слева-направо» попарно обходятся вершины, содержащие символы из алфавита терминалов Terminal и соответствующие им расположенные сверху вершины, содержащие символы из алфавита функционалов Functional. Затем при движении в том же направлении («снизу-вверх» и «слева-направо») попарно обходятся вершины, содержащие символы из алфавита арифметических операций Operation, и соответствующие им расположенные сверху вершины, содержащие символы из алфавита функционалов Functional [9 – 11].
Антитело (при движении по нему слева направо) в качестве первых двух символов содержит пару символов нулевого уровня СБД из алфавита функционалов Functional и алфавита арифметических операций Operation. Затем в антителе располагаются списки символов, соответствующие «правым» поддеревьям максимально возможного порядка `K=2` (при движении по СБД «сверху – вниз»), и, наконец, список символов, входящих в «левое» поддерево максимально возможного порядка `K=3` [9 – 11].
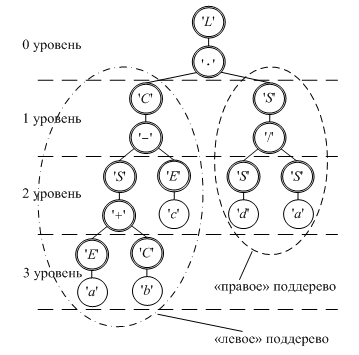
Рис. 2. Пример строго бинарного дерева
Так, антитело, сформированное на основе СБД, представленном на рисунке 2, кодируется строкой символов: `L*S"/"SeSdC-S+EaCbEa`, а соответствующая этому антителу МП 4-го порядка с учетом упорядоченности символов `a,b,c,d` в алфавите терминалов Terminal` ` может быть записана как:
` f(d^(j-1),d^(j-2),d^(j-3),d^(j-4),d^(j-5))= ln(cos(sin(exp(d^(j-1))+cos(d^(j-2)))-exp(d^(j-3)))*sin(sin(d^(j-4))/sin(d^(j-1)))`
МАКО включает в себя подготовительную часть, которая отвечает за формирование начальной популяции антител, и итерационную часть, в которой последовательно реализуются: упорядочение антител по возрастанию значений аффинитета `Aff`; отбор и клонирование части «лучших» антител (антител с наименьшими значениями аффинитета `Aff`); гипермутация клонов антител; самоуничтожение клонов антител, «похожих» на другие клоны и антитела текущей популяции; вычисление аффинитета клонов антител и формирование новой популяции антител (которая становится текущей популяцией антител для очередной итерации); супрессия текущей популяции антител; генерация новых антител и добавление их к текущей популяции до получения ее исходного размера; проверка условия завершения работы МАКО [10].
Существенный интерес представляет решение задачи среднесрочного прогнозирования временных рядов, входящих в группу `T`, с приемлемыми (для выполнения всех необходимых вычислений) временными затратами [13 – 15].
В качестве первого ПК МП предлагается использовать показатель аффинитета `Aff` (Affinity), основанный на расчете значения средней относительной ошибки прогнозирования (Average Forecasting Error Rate) `AFER` [16, 17]:
`AFER=100/(n-k)*sum_(j=k+1)^n|(f^j-d^j)/d^j|` (1)
где `d^j` и `f^j` – соответственно реальное (фактическое) и предсказанное значения для `j`-го элемента ВР; `n` – количество элементов ВР.
Для повышения точности прогнозов с применением МП на основе СБД и МАКО при решении задачи краткосрочного прогнозирования и обеспечения возможности применения этих моделей при решении задачи среднесрочного прогнозирования при оценке качества МП наряду с показателем аффинитета предлагается использовать еще один ПК – показатель несовпадения тенденций ВР `Tendency`, который может быть вычислен как [16, 17]:
`Tendency=h/(n-k-1)` , (2)
где `h` – количество отрицательных произведений `(f^(j-1)-f^j)*(d^(j-1)-d^j)` при `j=r+2,n`; `f^j` и `d^j` – предсказанное и реальное значения ВР для `j`-го отсчета времени; `n` – количество элементов ВР; `k` – порядок модели; `n-k-1` – общее количество произведений `(f^(j-1)-f^j)*(d^(j-1)-d^j)`.
Оба рассматриваемых ПК МП – `Aff ` (1) и `Tendency` (2) – реализуют оценку сходства моделируемого и реального ВР, но с применением разных принципов оценивания. Показатель аффинитета `Aff ` основан на учете сходства прогнозных и реальных значений известных элементов ВР, а показатель несовпадения тенденций `Tendency` – на учете сходства направлений изменения прогнозных и реальных значений известных элементов ВР (что позволяет проанализировать тенденции изменения ВР, а также наличие сезонных колебаний). При этом оба ПК должны быть минимизированы. Таким образом, при разработке МП на основе СБД и МАКО очевидна целесообразность реализации одновременного учета при оценке качества МП наряду со значением показателя аффинитета `Aff ` (1) еще и значения показателя несовпадения тенденций `Tendency` (2).
Использование дополнительного ПК позволит скорректировать направление поиска искомой МП, и, в итоге, сократить количество итераций для её определения. Для решения задачи одновременного учета двух ПК при разработке МП целесообразно использовать подход, предполагающий применение алгоритмов многоцелевой оптимизации (МЦО), в том числе, эволюционных алгоритмов [18 – 38], обеспечивающих решение проблемы учета нескольких целевых функций (критериев, ПК) при решении различных прикладных задач.
Наибольшее применение среди эволюционных алгоритмов МЦО в настоящее время находят ГА [18, 24 – 26, 28, 29, 32, 34]. Следует отметить и многоцелевые АКО [20, 21, 25, 30, 31, 38], однако они менее проработаны и, в своем большинстве, заимствуют принципы МЦО, заложенные в ГА. Возможность данного заимствования может быть объяснена многими сходными механизмами реализации эволюционного процесса в ГА и АКО.
На данный момент широко известны следующие ГА МЦО: VEGA (Vector Evaluated Genetic Algorithm) [38]; FFGA (Fonseca and Fleming’s Genetic Algorithm) [26]; NPGA (Niched Pareto Genetic Algorithm) [30]; NSGA (Non-dominated Sorting Genetic Algorithm) [32]; NSGA-II (Non-dominated Sorting Genetic Algorithm-II) [22]; NSGA-III (Non-dominated Sorting Genetic Algorithm-III) [23]; SPEA (Strength Pareto Evolutionary Algorithm) [34]. В качестве наиболее распространенных АКО МЦО следует указать: MISA (Multiobjective Immune System Algorithm) [35]; MOIA (Multiobjective Immune Algorithm) [33]; MOCSA (Multiobjective Clonal Selection Algorithm) [29]; IDCMA (Immune Dominance Clonal Multiobjective Algorithm) [30]; ACSAMO (Adaptive Clonal Selection Algorithm for Multiobjective Optimization) [36]; NNIA (Nondominated Neighbor Immune Algorithm) [37].
Анализ работ, посвященных вопросам применения МЦО на основе эволюционных алгоритмов, в частности, ГА [22, 23, 26, 30, 32, 34, 38] и АКО [29, 33, 35, 36, 37], показал, что преобладающее большинство алгоритмов основаны на принципах Парето-доминирования. В связи с этим был сделан вывод о перспективности использования принципов Парето-доминирования при усовершенствовании МАКО, применяемого для отбора МП на основе СБД. С учетом особенностей решаемой задачи и вычислительных характеристик ГА и АКО МЦО было принято решение о целесообразности адаптации идей, заложенных в алгоритм NSGA-II, который относится к группе алгоритмов МЦО, использующих принципы Парето-доминирования для определения целесообразности включения решения в следующее поколение популяции решений.
В соответствии с принципами Парето-доминирования будем говорить, что `z`-я МП доминирует над `s`-й МП (`s=1,S;" " z=1,S`), если `z`-я МП не хуже `s`-й МП по всем `v`-м (`v=1,V`) ПК и хотя бы по одному ПК превосходит `s`-ю МП, то есть для всех значений `v" "(v=1,V)` выполняется условие: `Q_(s,v)= > Q_(z,v)` и существует хотя бы один `v^("*")`-й `(1=<v^("*")=<V)` ПК, для которого `Q_(s,v*) > Q_(z,v*)`. При этом все ПК должны быть минимизированы [16]. При этом ранг `s`-й МП равен количеству МП в популяции, которые доминируют над `s`-й МП. Ранг недоминируемой `s`-й МП полагается равным нулю.
В случае когда число ПК МП равно 2 `(V=2)`, а `Q_(s,1)=Aff_s`, `Q_(s,2)=Tendency_s`, где `Aff_s` и `Tendency_s `– соответственно значения показателя аффинитета (1) и показателя несовпадения тенденций (2) для `s`-й МП (`s=1,S`), `s`-я МП доминируема `z`-й МП (`s=1,S;" "z=1,S`), если выполняются условия: (`Q_(s,1)>=Q_(z,1)` и `Q_(s,2)>Q_(z,2)`) или (`Q_(s,1)>Q_(z,1)` и `Q_(s,2)=>Q_(z,2)`), то есть (`Aff_s>=Aff_z` и `Tendency_s>Tendency_z`) или (`Aff_s>Aff_z` и `Tendency_s>=Tendency_z`) [16].
Также при анализе целесообразности использования МП в качестве антитела-родителя предлагается оценивать так называемое расстояние скученности, что позволит исключить возможность попадания МП в локальные минимумы. Расстояние скученности для `s` -й МП может быть вычислено как:
`tau_s=sum_(v=1)^V[(Q_(s-1,v)-Q_(s+1,v))/(Q_v^max-Q_v^min)]` , (3)
где `Q_(s-1,v)` и `Q_(s+1,v)` – значения `v`-го ПК `(v=1,V)` для МП c номерами `(s-1)` и `(s+1)`, являющихся «соседями» для `s`-й МП; `Q_v^min` и `Q_v^max`– минимальное и максимальное значения `v`-го ПК `(v=1,V)` соответственно.
Расстояние скученности для `s`-й МП с учетом двух ПК может быть вычислено как:
`tau_s=(Q_(s-1,1)-Q_(s+1,1))/(Q_1^max-Q_1^min)+(Q_(s-1,2)-Q_(s+1,2))/(Q_2^max-Q_2^min)` .
В итоге, при реализации расчетов `s`-я МП будет считаться лучшей, чем `z`-я модель, если: `R_s<R_z` или (`R_s=R_z` и `tau_s>tau_z`).
С учетом вышеизложенного многоцелевой МАКО (ММАКО) может быть описан следующей последовательностью шагов [16].
- Сгенерировать популяцию антител, каждое из которых кодируется на основе СБД и определяет некоторую МП.
- Отсортировать популяцию антител по «недоминированию» на основе значений двух ПК МП – значения показателя аффинитета `Aff ` (1) и значения показателя несовпадения тенденций `Tendency ` (2).
- Осуществить выбор антител-родителей для формирования следующего поколения антител-клонов на основе рангов и вычисленных «расстояний скученности», соответствующих МП для текущей популяции антител.
- Перейти к п. 5, если достигнуты желаемые значения ПК или исчерпано количество поколений в МАКО. В противном случае перейти к п. 2.
- Выбрать в последней популяции антител антитело с минимальным значением показателя аффинитета `Aff ` (1) и считать его искомым («лучшим») антителом. Использовать «лучшее» антитело для построения искомой МП с целью выполнения краткосрочных и среднесрочных прогнозов.
В результате реализации предлагаемого алгоритма будет получено Парето-множество недоминируемых (Парето-оптимальных) МП, обеспечивающих лучшие сочетания значений используемых ПК МП для рассматриваемого ВР.
Очевидно, что ММАКО требует больших вычислительных затрат по сравнению с исходным МАКО [9 – 11]. Для сокращения времени прогнозирования групп ВР предлагается использовать алгоритмы кластерного анализа. Такие алгоритмы, как алгоритм четких -средних, алгоритм нечетких -средних, EM-алгоритм и т.п. позволяют в ходе итерационных вычислений выполнить разбиение группы объектов на заранее заданное число кластеров «» в соответствии с некоторым критерием оптимальности [14, 15]. При этом определяются координаты центроидов кластеров. В контексте решения задачи кластеризации ВР координаты центроидов могут быть использованы для формирования обобщающих ВР-центроидов, характеризующих частные (отдельные) ВР, входящие в соответствующие кластеры (рисунок 3). Очевидно, что для ВР-центроида возможна разработка некоторой МП, которая в дальнейшем может быть использована либо непосредственно для прогнозирования частных ВР (отнесенных к данному кластеру), либо в качестве базовой модели – с целью ее дальнейшего уточнения и последующего применения для прогнозирования частных ВР.
Для учета степени актуальности значений элементов ВР в процессе кластеризации ВР, предлагается использовать модифицированную евклидову метрику:
`d(v_r,t_i)=sqrt(sum_(j=1)^n((j/n)*(v_r^j-t_i^j)^2)` (4)
где `d(v_r,t_i)` – расстояние между центром кластера `v_r` и объектом `t^i`; `n` – число характеристик объекта.
Целесообразность такой модификации евклидовой метрики объясняется тем, что при построении МП большее предпочтение следует отдавать самым близким к моменту прогнозирования элементам ВР. Использование весовых коэффициентов вида «`j"/"n`» позволяет считать наиболее значимыми расхождения между значениями самых актуальных элементов ВР (так, при `j=n` значение весового коэффициента равно «1», а при `j=1` – равно «`1"/"n`»).
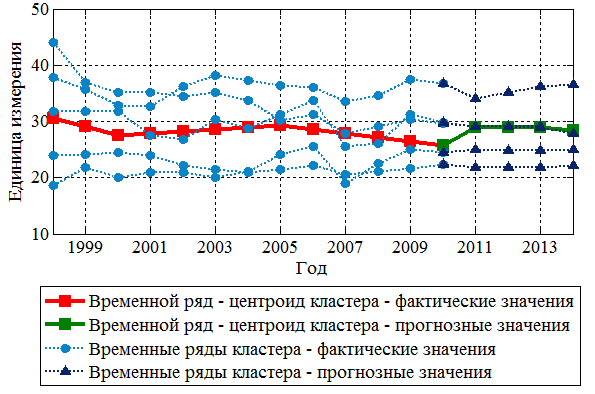
Рис. 3. Подгруппа временных рядов и ВР-центроид
Формула (4) позволяет не только удовлетворить требование учета актуальности элементов ВР, но и, ввиду высокой чувствительности к разнонаправленности тенденций ВР, обеспечивает объединение в кластеры на основе сходства тенденций [14, 15].
Еще одна проблема, возникающая в процессе кластеризации ВР, связана с их разной масштабностью по причине того, что они характеризуют те или иные показатели, имеющие различные единицы измерения, различные диапазоны изменения и соответствующие им статистические характеристики (математическое ожидание и т.п.).
Для решения этой проблемы целесообразно использование алгоритмов нормализации, которые широко применяются в статистике, математической экономике и эконометрике. Суть их состоит в определении некоторого среднего уровня – медианы, относительно которой выравниваются все анализируемые ВР [14, 15]. В качестве медианы может выступать, в частности, ВР-центроид `S`, элементы `S_j` которого определяются как:
`S_j=1/m*sum_(i=1)^m(t_i^j)` (5)
где `t_i^j` – `j`-й элемент `i`-го ВР; `i=1,m`; `j=1,n`; `m `– количество ВР; `n` – количество элементов ВР-центроида.
Преобразованные таким образом ВР в дальнейшем могут быть использованы для группирования ВР в кластеры с применением, например, алгоритма четких `c`-средних. Так как центроиды кластеров выражают общие тенденции для подгрупп ВР, формирующих соответствующие кластеры, то целесообразна разработка моделей прогнозирования на основе СБД и ММАКО для ВР-центроидов. При этом следует отметить, что прогнозирование ВР с использованием общих МП не ведет к получению одинаковых для подгруппы (кластера) ВР прогнозов. МП определяет лишь математический закон изменения значений элементов ВР посредством формируемой с применением ММАКО аналитической зависимости. Сами же прогнозные значения для каждого частного ВР будут уникальными, поскольку будут вычисляться при подстановке в общую МП известных значений элементов частного ВР. Экспериментальные исследования Апробация предлагаемого метода прогнозирования групп ВР была выполнена с использованием ВР для 19 макроэкономических показателей Российской Федерации, взятых с сайта World DataBank за период с 1999 г. по 2014 г. (http://databank.worldbank. org/data/views/reports/tableview. aspx?isshared=true#).
По результатам реализации алгоритма четких `c`-средних, в котором расстояния между ВР вычислялись в соответствии с формулой (4), все ВР были разделены на 6 кластеров (подгрупп ВР). Информация об их содержимом представлена в первом столбце табл. 1. Для каждой группы ВР были построены общие МП на основе одного и двух ПК. В каждом случае данные за период с 1999 г. по 2011 г. были использованы для разработки общих МП, а за период с 2011 г. по 2014 г. – для прогнозирования частных ВР, входящих в группу, на 5 шагов вперед. При этом по результатам прогнозирования на 5 шагов вперед была вычислена средняя относительная ошибка прогнозирования Error ` `:
Error= `100/5*sum_(j=k+1)^n|(f^j-d^j)/d^j|` (6)
в которой при `n=13` величины `f^j` и `d^j` с индексами `j=14`, `j=15` и `j=16` соответствовали предсказанному (прогнозному) и реальному значениям элементов ВР за 2012, 2013 и 2014 годы.
Таблица 1. Результаты прогнозирования макропоказателей с использованием одного ПК
|
№
п/п
|
Наименование
показателя
|
Единица
измерения
|
AFER,
%
|
1
|
2
|
3
|
4
|
5
|
Error
|
Tendency
|
|
1 кластер
|
|
1
|
Ожидаемая продолжительность жизни при рождении
|
Количество лет
|
1,46
|
5,11
|
3,42
|
4,47
|
4,48
|
5,11
|
4,52
|
0,3
|
|
2
|
Улучшенные средства санитарии
|
%
|
2,45
|
0,38
|
0,92
|
7
|
7,03
|
7,03
|
4,47
|
0,3
|
|
3
|
Добавленная стоимость в сфере услуг
|
% ВВП
|
0,28
|
6,34
|
2,18
|
3,99
|
0,64
|
2,25
|
30,8
|
0,5
|
|
Среднее значение по кластеру
|
1,40
|
3,94
|
2,17
|
5,16
|
4,05
|
4,80
|
4,02
|
0,37
|
|
2 кластер
|
|
4
|
Коэффициент подростковой фертильности (в возрасте 15-19 лет)
|
Число рождений на 1000 женщин
|
0,8
|
1,36
|
0,74
|
2,49
|
5,1
|
7,56
|
3,45
|
0,1
|
|
5
|
Экспорт товаров и услуг
|
% ВВП
|
1,35
|
4,19
|
9,03
|
1,86
|
11,5
|
0,97
|
5,51
|
0,2
|
|
6
|
Доходы, за исключением грантов
|
% ВВП
|
1,32
|
4,46
|
2,91
|
1,55
|
5,17
|
4,51
|
3,72
|
0,3
|
|
7
|
Смертность в возрасте до 5 лет
|
%
|
1,43
|
5,14
|
2,52
|
4,04
|
1,48
|
0,59
|
2,75
|
0,2
|
|
8
|
Добавленная стоимость в промышленности
|
% ВВП
|
1,17
|
7,14
|
6,96
|
7,91
|
2,82
|
2,46
|
5,46
|
0,5
|
|
Среднее значение по кластеру
|
1,21
|
4,46
|
4,43
|
3,57
|
5,21
|
3,22
|
4,18
|
0,26
|
|
3 кластер
|
|
9
|
Коэффициент рождаемости
|
Число рождений на 1000 женщин
|
2,81
|
0,63
|
5,63
|
10,93
|
4,63
|
5,79
|
5,52
|
0,1
|
|
10
|
Военные расходы
|
% ВВП
|
1,08
|
5,14
|
2
|
4,16
|
2,28
|
5,79
|
3,87
|
0,5
|
|
Среднее значение по кластеру
|
1,95
|
2,88
|
3,81
|
7,54
|
3,45
|
5,79
|
4,70
|
0,30
|
|
4 кластер
|
|
11
|
Экспорт высоких технологий
|
%
|
1,11
|
4,25
|
8,33
|
6,53
|
6,15
|
3,5
|
5,75
|
0,56
|
|
12
|
Начало процедур для регистрации бизнеса
|
Количество
|
0,29
|
0
|
0
|
0,63
|
14,29
|
8,06
|
4,59
|
0
|
|
Среднее значение по кластеру
|
0,70
|
2,13
|
4,17
|
3,58
|
10,22
|
5,78
|
5,17
|
0,28
|
|
5 кластер
|
|
13
|
Валовое накопление капитала
|
% ВВП
|
1,57
|
1,08
|
0,98
|
0,48
|
0,48
|
1,01
|
0,81
|
0,2
|
|
14
|
Импорт товара и услуг
|
% ВВП
|
0,47
|
4,24
|
5,56
|
4,61
|
5,21
|
4,66
|
4,86
|
0,45
|
|
Среднее значение по кластеру
|
1,02
|
2,66
|
3,27
|
2,55
|
2,85
|
2,83
|
2,83
|
0,33
|
|
6 кластер
|
|
15
|
Процент иммунизации против кори
|
%
|
2,01
|
4,08
|
4,08
|
3,77
|
3,77
|
3,11
|
3,76
|
0
|
|
16
|
Количество деторождений при помощи квалифицированного медицинского персонала
|
%
|
0,01
|
0
|
0
|
0,16
|
0,21
|
0,28
|
0,13
|
0
|
|
17
|
Соотношение девочек и мальчиков в системе начального и среднего образования
|
%
|
0,05
|
0,2
|
0,3
|
0,43
|
0,01
|
1,02
|
0,39
|
0,4
|
|
18
|
Улучшенные источники воды
|
%
|
0,04
|
1,24
|
2,06
|
1,26
|
1,8
|
1,5
|
1,57
|
0,1
|
|
19
|
Процент населения, имеющее начальное образование, всего
|
%
|
0,17
|
1,56
|
4,74
|
0
|
0,01
|
1,27
|
1,51
|
0,56
|
|
Среднее значение по кластеру
|
0,46
|
1,42
|
2,24
|
1,12
|
1,16
|
1,44
|
1,47
|
0,22
|
Таблица 2. Результаты прогнозирования макропоказателей с использованием двух ПК
|
№
п/п
|
Наименование
показателя
|
Единица
измерения
|
AFER,
%
|
1
|
2
|
3
|
4
|
5
|
Error
|
Tendency
|
|
1-й кластер
|
|
1
|
Ожидаемая продолжительность жизни при рождении
|
Количество лет
|
0,09
|
5,55
|
3,89
|
4,40
|
4,20
|
3,35
|
4,28
|
0,1
|
|
2
|
Улучшенные средства санитарии
|
%
|
0,24
|
2,32
|
0,67
|
2,36
|
2,03
|
3,54
|
2,18
|
0,2
|
|
3
|
Добавленная стоимость в сфере услуг
|
% ВВП
|
0,15
|
1,89
|
0,98
|
1,58
|
0,79
|
1,88
|
1,42
|
0,5
|
|
Среднее значение по кластеру
|
0,16
|
3,25
|
1,84
|
2,78
|
2,34
|
2,92
|
2,63
|
0,27
|
|
2-й кластер
|
|
4
|
Коэффициент подростковой фертильности (в возрасте 15-19 лет)
|
Число рождений на 1000 женщин
|
0,18
|
0,11
|
3,04
|
1,45
|
4,86
|
1,93
|
2,28
|
0
|
|
5
|
Экспорт товаров и услуг
|
% ВВП
|
0,8
|
1,66
|
0,34
|
0,03
|
2,51
|
1,93
|
1,29
|
0
|
|
6
|
Доходы, за исключением грантов
|
% ВВП
|
1,15
|
5,21
|
3,72
|
4,68
|
5,17
|
5,89
|
4,93
|
0
|
|
7
|
Смертность в возрасте до 5 лет
|
%
|
0,47
|
2,08
|
0,00
|
5,88
|
3,19
|
2,52
|
2,74
|
0,2
|
|
8
|
Добавленная стоимость в промышленности
|
% ВВП
|
0,18
|
3,64
|
5,57
|
0,35
|
4,78
|
4,59
|
3,79
|
0
|
|
Среднее значение по кластеру
|
0,63
|
2,54
|
2,53
|
2,48
|
4,10
|
3,37
|
3,01
|
0,04
|
|
3 кластер
|
|
9
|
Коэффициент рождаемости
|
Число рождений на 1000 женщин
|
0,72
|
0,63
|
1,88
|
9,29
|
0,00
|
0,83
|
2,52
|
0,2
|
|
10
|
Военные расходы
|
% ВВП
|
1,42
|
2,97
|
5,50
|
1,47
|
3,58
|
0,76
|
2,86
|
0,1
|
|
Среднее значение по кластеру
|
1,07
|
1,80
|
3,69
|
5,38
|
1,79
|
0,79
|
2,69
|
0,05
|
|
4 кластер
|
|
11
|
Экспорт высоких технологий
|
%
|
0,51
|
2,63
|
2,62
|
0,48
|
1,56
|
3,85
|
2,23
|
0,2
|
|
12
|
Начало процедур для регистрации бизнеса
|
Количество
|
0,67
|
1,88
|
1,88
|
1,26
|
0,71
|
0,38
|
1,22
|
0,1
|
|
Среднее значение по кластеру
|
0,59
|
2,25
|
2,25
|
0,87
|
1,14
|
2,12
|
1,72
|
0,15
|
|
5 кластер
|
|
13
|
Валовое накопление капитала
|
% ВВП
|
1,09
|
0,40
|
1,63
|
3,01
|
2,85
|
2,66
|
2,11
|
0,2
|
|
14
|
Импорт товара и услуг
|
% ВВП
|
1,04
|
2,30
|
3,59
|
4,11
|
1,69
|
3,61
|
3,06
|
0,1
|
|
Среднее значение по кластеру
|
1,07
|
1,35
|
2,61
|
3,56
|
2,27
|
3,13
|
2,58
|
0,15
|
|
6 кластер
|
|
15
|
Процент иммунизации против кори
|
%
|
0,04
|
0,51
|
0,51
|
0,84
|
0,84
|
0,12
|
0,56
|
0
|
|
16
|
Количество деторождений при помощи квалифицированного медицинского персонала
|
%
|
0,01
|
0,15
|
0,10
|
0,11
|
0,16
|
0,20
|
0,14
|
0,1
|
|
17
|
Соотношение девочек и мальчиков в системе начального и среднего образования
|
%
|
0,04
|
0,05
|
0,25
|
0,17
|
0,45
|
1,91
|
0,57
|
0,1
|
|
18
|
Улучшенные источники воды
|
%
|
0,04
|
0,62
|
0,41
|
0,51
|
0,06
|
0,17
|
0,35
|
0,2
|
|
19
|
Процент населения, имеющее начальное образование, всего
|
%
|
1,22
|
1,24
|
4,74
|
3,01
|
2,05
|
2,06
|
2,62
|
0,2
|
|
Среднее значение по кластеру
|
0,27
|
0,51
|
1,20
|
0,93
|
0,71
|
0,89
|
0,85
|
0,12
|
В табл. 1 и 2 приведены значения показателей `Aff` `(AFER)` и `Tendency` при `n=13` за период с 1999 г. по 2011 г.; значения Error средних относительных ошибок прогнозирования на 5 шагов вперед за период с 2011 г. по 2014 г.; средние значения `AFER`, `Tendency` и Error по каждому кластеру и по всем кластерам в целом по результатам построения МП по одному и двум ПК соответственно.
Сравнив значения средней относительной ошибки прогнозирования на 5 шагов вперед (рисунок 4), показателя аффинитета (рисунок 5) и показателя несовпадения тенденций (рисунок 6), можно сделать следующие выводы:
- учет нескольких ПК при построении МП ведет к уменьшению ошибки прогнозирования как при среднесрочном, так и при краткосрочном прогнозировании;
- учет дополнительного ПК МП – показателя несовпадения тенденций, позволяет сохранять низкий уровень значений ошибки прогнозирования при увеличении горизонта прогнозирования.
Рис. 4. Сравнение значений средней относительной ошибки прогнозирования
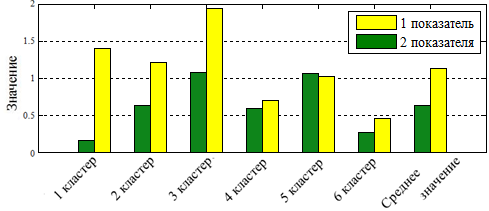
Рис. 5. Сравнение значений показателя аффинитета
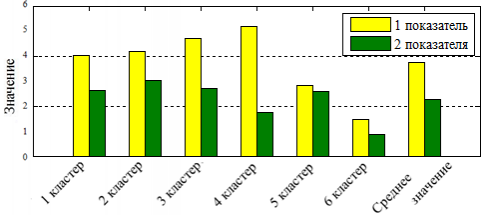
Рис. 6. Сравнение значений показателя несовпадения тенденций
В рассматриваемом примере было выполнено 400 итераций МАКО для популяции из 20 антител при коэффициентах клонирования антител и размножения клонов, равных соответственно 0,3 и 0,8. Была использована ПЭВМ, работающая под 64-разрядной версией Windows 7, с оперативной памятью 2 Гб и двухядерным процессором Pentium 4 с тактовой частотой каждого ядра 3,4 ГГц. В этом случае на построение одной МП потребовалось 77 секунд. Таким образом, для построения 6 общих МП необходимо 462 секунд (7 минут 42 секунды), а для построения 19 индивидуальных МП потребовалась бы 1 463 секунда (24 минут 23 секунды), что больше в 3,2 раза.
При реализации предлагаемого метода прогнозирования групп ВР необходимы дополнительные временные затраты, обусловленные необходимостью выполнения процедуры кластеризации ВР. Однако, время, затрачиваемое на процедуру кластеризации, в рассматриваемом примере составляет всего 0,254 секунды. Это гораздо меньше времени, которое необходимо потратить на построение еще 19 МП (это время составляет 1463 секунды, т.е. 24 минуты 23 секунды). При этом при выполнении расчетов использовалась среда программирования системы инженерных и научных расчетов MATLAB R2009b. Заключение Предлагаемый метод прогнозирования групп ВР реализует совместное применение алгоритма четких с-средних и моделей прогнозирования на основе СБД и ММАКО. Это позволяет обеспечить получение индивидуальных (частных) прогнозных значений в краткосрочной и среднесрочной перспективе для всех ВР группы с приемлемыми временными затратами. При этом очевидна возможность реализации распараллеливания вычислений, что позволит увеличить скорость выполнения расчетов.
Результаты вычислительных экспериментов, полученные в ходе прогнозирования макроэкономических показателей Российской Федерации, подтверждают перспективность применения и дальнейшего развития предлагаемого метода прогнозирования групп ВР. При этом требуемая точность прогноза для частного ВР может быть достигнута в процессе уточнения общей МП с применением ММАКО.
Работа поддержана грантом РФФИ, номер 16-08-00771, тема «Интеллектуальные программно-математические средства индивидуального и группового прогнозирования временных рядов».
Библиография
|
1.
|
Андерсен Т. Статистический анализ временных рядов. Москва: Мир. 1976. 756 с.
|
|
2.
|
Белов В.В. Проблемы факторного прогнозирования социально-экономических показателей // Вестник Московского государственного университета приборостроения и информатики. 2005. № 2. С. 116–122.
|
|
3.
|
Терехов А.А. Идентификация статистического материала и консолидация временных рядов // Вестник Рязанского государственного радиотехнического университета. 2009. № 27. С. 62–70.
|
|
4.
|
Петрушин В.Н., Рытиков Г.О. Формализация временного ряда методом двойного сглаживания // Cloud of Science. 2014. Т. 1.№ 2. С. 230–238.
|
|
5.
|
Демидова Л. А. Разработка однофакторных нечетких моделей для анализа тенденций временных рядов с использованием генетического алгоритма // Научно-технические ведомости СПбГПУ. 2007. № 52-2. С. 156–164.
|
|
6.
|
Demidova L.A. Genetic Algorithm For Optimal Parameters Search In The One-Factor Forecasting Model Based On Continuous Type-2 Fuzzy Sets // Automation and Remote Control. 2013. Т. 74. № 2. С. 313–320.
|
|
7.
|
Паклин Н.Б. Бизнес-аналитика от данных к знаниям / Паклин Н.Б., Орешков В.И. Санкт-Петербург: Питер, 2013. 704 с.
|
|
8.
|
Чубукова И.А. Data Mining: учеб. пособие. М.: Интернет-университет информационных технологий: БИНОМ: Лаборатория знаний. 2006. 382 с.
|
|
9.
|
Демидова Л.А., Корячко А.В., Скворцова Т.С. Модифицированный алгоритм клонального отбора для анализа временных рядов с короткой длиной актуальной части // Системы управления и информационные технологии. 2010. Т. 42. № 4.1. С. 131–136.
|
|
10.
|
Демидова Л. А. Модели прогнозирования временных рядов с короткой актуальной частью на основе модифицированного алгоритма клонального отбора // Вестник Рязанского государственного радиотехнического университета. 2012. № 39-2. С. 64–71.
|
|
11.
|
Демидова Л.А. Оценка качества моделей прогнозирования на основе строго бинарных деревьев и модифицированного алгоритма клонального отбора // Cloud of Science. 2014. Т. 1. № 2. С. 202–222.
|
|
12.
|
Demidova L.A. Time series forecasting models on the base of modified clonal selection algorithm // В сборнике: 2014 International conference on computer technologies in physical and engineering applications (ICCTPEA) Editor: E. I. Veremey. Санкт-Петербургский государственный университет; IEEE (IEEE Catalog number CFP14BDA-USB). 2014. С. 33–34.
|
|
13.
|
Астахова Н.Н., Демидова Л.А. Метод прогнозирования групп временных рядов с применением алгоритмов кластерного анализа // Прикаспийский журнал Управление и высокие технологии. 2015. № 2. С. 59–79.
|
|
14.
|
Astakhova N.N., Demidova L.A., Nikulchev E.V. Forecasting Method For Grouped Time Series With The Use Of K-Means Algorithm // Applied Mathematical Sciences, Vol. 9, no. 97. 2015, p. 4813–4830.
|
|
15.
|
Astakhova N.N., Demidova L.A., Nikulchev E.V. Forecasting Of Time Series' Groups With Application Of Fuzzy C-Mean Algorithm // Contemporary Engineering Sciences, Vol. 8, no 35. 2015, p. 1659–1677.
|
|
16.
|
Демидова Л.А., Астахова Н.Н. Многоцелевая оптимизация для моделей прогнозирования на основе строго бинарных деревьев // Вестник Рязанского государственного радиотехнического университета. 2016. № 55. С. 118-130.
|
|
17.
|
Астахова Н.Н., Демидова Л.А. Cравнительный анализ вариантов оптимизации при разработке моделей прогнозирования на основе строго бинарных деревьев // Прикаспийский журнал: управление и высокие технологии. 2016. № 2 (34). С. 9–25.
|
|
18.
|
Bentley P.J., Wakefield J.P. Finding Acceptable Solutions in the Pareto-Optimal Range using Multiobjective Genetic Algorithms // In Proceedings of the 2nd On-Line World Conference on Soft Computing in Engineering Design and Manufacturing. 1997. pp. 126–140.
|
|
19.
|
Branke J. Memory Enchanced Evolutionary Algorithms for Changing Optimization Problems, Institute AIFB, University of Karlsruhe, 1999. pp. 1049–1063.
|
|
20.
|
Coello Coello C.A., Cruz Cortés N. An approach to solve multiobjective optimization problems based on an artificial immune system // Proceedings of the First International Conference on Artificial Immune Systems, University of Kent at Canterbury, UK, September 9–11. 2002. pp. 212–221.
|
|
21.
|
Campelo, F., Guimarães, F. G., Saldanha, R. R., Igarashi, H., Noguchi, S., Lowther, D. A., & Ramirez, J. A. A novel multiobjective immune algorithm using nondominated sorting. In 11th International // IGTE Symposium on Numerical Field Calculation in Electrical Engineering. 2004.
|
|
22.
|
Deb K., Pratap A., Agarwal S., Meyarivan T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA II // KanGAL Report No. 200001. Indian Institute of Technology. Kanpur, India. 2000. pp. 182–197.
|
|
23.
|
Deb K., Jain H. An evolutionary many-objective optimization algorithm using reference-point based non-dominated sorting approach, Part I: Solving problems with box constraints. IEEE Transactions on Evolutionary Computation. 2014. Vol. 18(4). pp. 577–601.
|
|
24.
|
Deb K. Multiobjective Optimization using Evolutionary Algorithms. Chichester. UK: Wiley. 2001. pp. 221–232.
|
|
25.
|
Eberhart R.C., Kennedy J. A new optimizer using particle swarm theory //Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, Piscataway, NJ: IEEE Service Center. 1995. pp. 39-43.
|
|
26.
|
Fonseca C.M., Fleming P.J. Multiobjective optimization and multiple constraint han-dling with evolutionary algorithms-Part I: A unified formulation // Technical report 564. University of Sheffield, Sheffield. UK. January. 1995. pp. 1–16.
|
|
27.
|
Goldberg D.E. Genetic Algorithms in Search, Optimization, and Machine Learning // Reading. Massachusetts: Addison-Wesley. 1989. 372 p.
|
|
28.
|
Jiao L., Gong M., Shang R., Du H., Lu B. Clonal selection with immune dominance and anergy based multiobjective optimization // 3rd International Conference on Evolutionary Multi-Criterion Optimization. 2005. pp. 474–489.
|
|
29.
|
Jiao L., Gong M., Du H., Bo L. Multiobjective immune algorithm with nondominated neighbor-based selection // Evolutionary Computation. Vol. 16. Issue 2. Summer. 2008. pp. 225–255.
|
|
30.
|
Horn J., Nafpliotis N., Goldberg D.E. A niched Pareto genetic algorithm for multiobjective optimization // In Proceedings of the First IEEE Conference on Evolutionary Computation. Piscataway. Vol. 1. 1994. pp. 82–87.
|
|
31.
|
Kennedy J., Eberhart R. C. A discrete binary version of the particle swarm algorithm // Proc. 1997 Conf. on Systems, Man, and Cybernetics Piscataway, NJ: IEEE Service Center. 1997. pp. 4104–4109.
|
|
32.
|
Knowles J., Corne D. The Pareto archived evolution strategy: A new baseline algorithm for multiobjective optimization // Proceedings of the 1999 Congress on Evolutionary Computation. Piscataway. New Jersey: IEEE Service Center. 1999. pp. 98–105.
|
|
33.
|
Luh G.-C., Chueh C.-H., Liu W.-W. MOIA: Multi-Objective Immune Alghorithm //Computers and Structures Vol. 82. 2004. pp. 829–844.
|
|
34.
|
Zitzler E., Thiele L. Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach. IEEE transactions on evolutionary computation. 1999. pp. 257–271.
|
|
35.
|
Srinivas N., Deb K. Multiple-Objective function optimization using non-dominated sorting genetic algorithms //Evolutionary Computation. Vol. 2. 1995. pp. 221–248.
|
|
36.
|
Wang, X. L., & Mahfouf, M. ACSAMO: An Adaptive Multiobjective Optimization Algorithm using the Clonal Selection Principle //2nd European Symposium on Nature-Inspired Smart Information Systems. 2006. pp. 1–12.
|
|
37.
|
Zhang, Z. Constrained Multiobjective Optimization Immune Algorithm: Convergence and Application //Computers and Mathematics with Applications. 2006. Vol. 52(5). pp. 791–808.
|
|
38.
|
Schaffer, J.D. Multiple objective optimization with vector evaluated genetic algorithms // In J. J. Grefenstette (Ed.), Proceedings of an International Conference on Genetic Algorithms and Their Applications, Pittsburgh, PA, 1985. pp. 93–100.
|
References
|
1.
|
Andersen T. Statisticheskii analiz vremennykh ryadov. Moskva: Mir. 1976. 756 s.
|
|
2.
|
Belov V.V. Problemy faktornogo prognozirovaniya sotsial'no-ekonomicheskikh pokazatelei // Vestnik Moskovskogo gosudarstvennogo universiteta priborostroeniya i informatiki. 2005. № 2. S. 116–122.
|
|
3.
|
Terekhov A.A. Identifikatsiya statisticheskogo materiala i konsolidatsiya vremennykh ryadov // Vestnik Ryazanskogo gosudarstvennogo radiotekhnicheskogo universiteta. 2009. № 27. S. 62–70.
|
|
4.
|
Petrushin V.N., Rytikov G.O. Formalizatsiya vremennogo ryada metodom dvoinogo sglazhivaniya // Cloud of Science. 2014. T. 1.№ 2. S. 230–238.
|
|
5.
|
Demidova L. A. Razrabotka odnofaktornykh nechetkikh modelei dlya analiza tendentsii vremennykh ryadov s ispol'zovaniem geneticheskogo algoritma // Nauchno-tekhnicheskie vedomosti SPbGPU. 2007. № 52-2. S. 156–164.
|
|
6.
|
Demidova L.A. Genetic Algorithm For Optimal Parameters Search In The One-Factor Forecasting Model Based On Continuous Type-2 Fuzzy Sets // Automation and Remote Control. 2013. T. 74. № 2. S. 313–320.
|
|
7.
|
Paklin N.B. Biznes-analitika ot dannykh k znaniyam / Paklin N.B., Oreshkov V.I. Sankt-Peterburg: Piter, 2013. 704 s.
|
|
8.
|
Chubukova I.A. Data Mining: ucheb. posobie. M.: Internet-universitet informatsionnykh tekhnologii: BINOM: Laboratoriya znanii. 2006. 382 s.
|
|
9.
|
Demidova L.A., Koryachko A.V., Skvortsova T.S. Modifitsirovannyi algoritm klonal'nogo otbora dlya analiza vremennykh ryadov s korotkoi dlinoi aktual'noi chasti // Sistemy upravleniya i informatsionnye tekhnologii. 2010. T. 42. № 4.1. S. 131–136.
|
|
10.
|
Demidova L. A. Modeli prognozirovaniya vremennykh ryadov s korotkoi aktual'noi chast'yu na osnove modifitsirovannogo algoritma klonal'nogo otbora // Vestnik Ryazanskogo gosudarstvennogo radiotekhnicheskogo universiteta. 2012. № 39-2. S. 64–71.
|
|
11.
|
Demidova L.A. Otsenka kachestva modelei prognozirovaniya na osnove strogo binarnykh derev'ev i modifitsirovannogo algoritma klonal'nogo otbora // Cloud of Science. 2014. T. 1. № 2. S. 202–222.
|
|
12.
|
Demidova L.A. Time series forecasting models on the base of modified clonal selection algorithm // V sbornike: 2014 International conference on computer technologies in physical and engineering applications (ICCTPEA) Editor: E. I. Veremey. Sankt-Peterburgskii gosudarstvennyi universitet; IEEE (IEEE Catalog number CFP14BDA-USB). 2014. S. 33–34.
|
|
13.
|
Astakhova N.N., Demidova L.A. Metod prognozirovaniya grupp vremennykh ryadov s primeneniem algoritmov klasternogo analiza // Prikaspiiskii zhurnal Upravlenie i vysokie tekhnologii. 2015. № 2. S. 59–79.
|
|
14.
|
Astakhova N.N., Demidova L.A., Nikulchev E.V. Forecasting Method For Grouped Time Series With The Use Of K-Means Algorithm // Applied Mathematical Sciences, Vol. 9, no. 97. 2015, p. 4813–4830.
|
|
15.
|
Astakhova N.N., Demidova L.A., Nikulchev E.V. Forecasting Of Time Series' Groups With Application Of Fuzzy C-Mean Algorithm // Contemporary Engineering Sciences, Vol. 8, no 35. 2015, p. 1659–1677.
|
|
16.
|
Demidova L.A., Astakhova N.N. Mnogotselevaya optimizatsiya dlya modelei prognozirovaniya na osnove strogo binarnykh derev'ev // Vestnik Ryazanskogo gosudarstvennogo radiotekhnicheskogo universiteta. 2016. № 55. S. 118-130.
|
|
17.
|
Astakhova N.N., Demidova L.A. Cravnitel'nyi analiz variantov optimizatsii pri razrabotke modelei prognozirovaniya na osnove strogo binarnykh derev'ev // Prikaspiiskii zhurnal: upravlenie i vysokie tekhnologii. 2016. № 2 (34). S. 9–25.
|
|
18.
|
Bentley P.J., Wakefield J.P. Finding Acceptable Solutions in the Pareto-Optimal Range using Multiobjective Genetic Algorithms // In Proceedings of the 2nd On-Line World Conference on Soft Computing in Engineering Design and Manufacturing. 1997. pp. 126–140.
|
|
19.
|
Branke J. Memory Enchanced Evolutionary Algorithms for Changing Optimization Problems, Institute AIFB, University of Karlsruhe, 1999. pp. 1049–1063.
|
|
20.
|
Coello Coello C.A., Cruz Cortés N. An approach to solve multiobjective optimization problems based on an artificial immune system // Proceedings of the First International Conference on Artificial Immune Systems, University of Kent at Canterbury, UK, September 9–11. 2002. pp. 212–221.
|
|
21.
|
Campelo, F., Guimarães, F. G., Saldanha, R. R., Igarashi, H., Noguchi, S., Lowther, D. A., & Ramirez, J. A. A novel multiobjective immune algorithm using nondominated sorting. In 11th International // IGTE Symposium on Numerical Field Calculation in Electrical Engineering. 2004.
|
|
22.
|
Deb K., Pratap A., Agarwal S., Meyarivan T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA II // KanGAL Report No. 200001. Indian Institute of Technology. Kanpur, India. 2000. pp. 182–197.
|
|
23.
|
Deb K., Jain H. An evolutionary many-objective optimization algorithm using reference-point based non-dominated sorting approach, Part I: Solving problems with box constraints. IEEE Transactions on Evolutionary Computation. 2014. Vol. 18(4). pp. 577–601.
|
|
24.
|
Deb K. Multiobjective Optimization using Evolutionary Algorithms. Chichester. UK: Wiley. 2001. pp. 221–232.
|
|
25.
|
Eberhart R.C., Kennedy J. A new optimizer using particle swarm theory //Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, Piscataway, NJ: IEEE Service Center. 1995. pp. 39-43.
|
|
26.
|
Fonseca C.M., Fleming P.J. Multiobjective optimization and multiple constraint han-dling with evolutionary algorithms-Part I: A unified formulation // Technical report 564. University of Sheffield, Sheffield. UK. January. 1995. pp. 1–16.
|
|
27.
|
Goldberg D.E. Genetic Algorithms in Search, Optimization, and Machine Learning // Reading. Massachusetts: Addison-Wesley. 1989. 372 p.
|
|
28.
|
Jiao L., Gong M., Shang R., Du H., Lu B. Clonal selection with immune dominance and anergy based multiobjective optimization // 3rd International Conference on Evolutionary Multi-Criterion Optimization. 2005. pp. 474–489.
|
|
29.
|
Jiao L., Gong M., Du H., Bo L. Multiobjective immune algorithm with nondominated neighbor-based selection // Evolutionary Computation. Vol. 16. Issue 2. Summer. 2008. pp. 225–255.
|
|
30.
|
Horn J., Nafpliotis N., Goldberg D.E. A niched Pareto genetic algorithm for multiobjective optimization // In Proceedings of the First IEEE Conference on Evolutionary Computation. Piscataway. Vol. 1. 1994. pp. 82–87.
|
|
31.
|
Kennedy J., Eberhart R. C. A discrete binary version of the particle swarm algorithm // Proc. 1997 Conf. on Systems, Man, and Cybernetics Piscataway, NJ: IEEE Service Center. 1997. pp. 4104–4109.
|
|
32.
|
Knowles J., Corne D. The Pareto archived evolution strategy: A new baseline algorithm for multiobjective optimization // Proceedings of the 1999 Congress on Evolutionary Computation. Piscataway. New Jersey: IEEE Service Center. 1999. pp. 98–105.
|
|
33.
|
Luh G.-C., Chueh C.-H., Liu W.-W. MOIA: Multi-Objective Immune Alghorithm //Computers and Structures Vol. 82. 2004. pp. 829–844.
|
|
34.
|
Zitzler E., Thiele L. Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach. IEEE transactions on evolutionary computation. 1999. pp. 257–271.
|
|
35.
|
Srinivas N., Deb K. Multiple-Objective function optimization using non-dominated sorting genetic algorithms //Evolutionary Computation. Vol. 2. 1995. pp. 221–248.
|
|
36.
|
Wang, X. L., & Mahfouf, M. ACSAMO: An Adaptive Multiobjective Optimization Algorithm using the Clonal Selection Principle //2nd European Symposium on Nature-Inspired Smart Information Systems. 2006. pp. 1–12.
|
|
37.
|
Zhang, Z. Constrained Multiobjective Optimization Immune Algorithm: Convergence and Application //Computers and Mathematics with Applications. 2006. Vol. 52(5). pp. 791–808.
|
|
38.
|
Schaffer, J.D. Multiple objective optimization with vector evaluated genetic algorithms // In J. J. Grefenstette (Ed.), Proceedings of an International Conference on Genetic Algorithms and Their Applications, Pittsburgh, PA, 1985. pp. 93–100.
|
Ссылка на эту статью
Просто выделите и скопируйте ссылку на эту статью в буфер обмена. Вы можете также
попробовать найти похожие
статьи
|





