|
ГЛАВНАЯ
> Вернуться к содержанию
Кибернетика и программирование
Правильная ссылка на статью:
Перминова М.Ю.
Анализ алгоритма декомпозиции полиномов, основанного на разбиениях
// Кибернетика и программирование.
2015. № 6.
С. 21-34.
DOI: 10.7256/2306-4196.2015.6.17169 URL: https://nbpublish.com/library_read_article.php?id=17169
Анализ алгоритма декомпозиции полиномов, основанного на разбиениях
Перминова Мария Юрьевна
аспирант, кафедра промышленной электроники, Томский государственный университет систем управления и радиоэлектроники
634045, Россия, Томская область, г. Томск, пр. Ленина, 40
Perminova Maria Yur'evna
graduate student, Department of Industrial Electronics, Tomsk State University of Control Systems and Radioelectronics
634045, Russia, Tomskaya oblast', g. Tomsk, pr. Lenina, 40

|
mary42rus@gmail.com
|
|
 |
|
DOI: 10.7256/2306-4196.2015.6.17169
Дата направления статьи в редакцию:
02-12-2015
Дата публикации:
19-01-2016
Аннотация:
Объектом исследования являются производящие функции, которые представляют собой эффективный инструмент решения разнообразных математических задач комбинаторики, теории вероятности, математической физики, анализа алгоритмов и т. д. Предметом исследования является один из классов производящих функций - полиномы. Особое внимание уделяется задаче декомпозиции полиномов, которая имеет множество решений. Для решения этой задачи предлагается новый алгоритм декомпозиции полиномов, основанный на разбиениях. Приводятся его краткое описание и пример работы. Определяется вычислительная сложность данного алгоритма, которая состоит из временных сложностей генерации разбиений, получения монома и решения уравнения. Временная сложность алгоритма декомпозиции полиномов, основанного на разбиениях, рассчитана на основании результатов, полученных Д. Кнутом и представленных в энциклопедии целочисленных последовательностей. Представлен оригинальный алгоритм нахождения декомпозиции полинома. Показано, что временная сложность алгоритма равна O(n^2). Проведено сравнение алгоритма с его аналогами. Анализ показал, что большинство алгоритмов декомпозиции полиномов имеют вычислительную сложность O(n^2). Представлены экспериментальные кривые вычислительной сложности алгоритма декомпозиции полиномов, основанного на разбиениях, и известных алгоритмов.
Ключевые слова:
декомпозиция полиномов, генерация разбиений, алгоритм, вычислительная сложность алгоритма, производящие функции, полином, системы компьютерной алгебры, композиция, моном, решение уравнений
УДК: 519.16:004.02
Abstract: The research focuses on the generating function, which is an effective tool for solving various mathematical problems in combinatorics, probability theory, mathematical physics, analysis of algorithms, etc. The subject of research is one class of generating functions – polynomials. Special attention is paid to the problem of polynomial decomposition, which has a number of solutions. The author proposes a new polynomial decomposition algorithm based on partitions. The article gives a brief description of the algorithm and gives an example of its usage. The study determines computational complexity of the algorithm, which consists of the time complexity of generating partitions, producing a monomial and solving the equation. The time complexity of the polynomial decomposition algorithm based on partitions is calculated on the basis of the results obtained by D. Knuth and given in the On-Line Encyclopedia of Integer Sequences. The original polynomial decomposition algorithm is also given. It is shown that the time complexity of the algorithm is O (n^2). The author compares the described algorithm with its analogs. The analysis shows that most of the decomposition algorithms have polynomial computational complexity of O (n^2). The experimental curves of the computational complexity of the polynomial decomposition algorithm based on partitions and known algorithms are shown.
Keywords: Decomposition of polynomials, Generation of partitions, algorithm, the computational complexity of the algorithm, generating functions, polynomial, computer algebra systems, composition, monomial, solution of equations
Введение В настоящее время при решении задач моделирования и математического анализа широко применяются системы компьютерной алгебры, относящиеся к классу систем символьных вычислений [1,2,3]. Одной из функций таких систем является представление полинома `F(x)` в виде композиции двух полиномов `B(A(x))`. Задача представления полинома `F( x)` в виде композиции двух полиномов `B(A(x))` имеет множество решений [4,5,6,7]. Для решения этой задачи предложен новый алгоритм (рис. 1), основанный на использовании методов нахождения коэффициентов композиции производящих функций [8] и на генерации разбиений [9]. На вход алгоритма подается исходный полином `F(x)`, на выходе получаются два полинома, композиция которых представляет собой полином `F(x)` [10].
|
GetDecomposition(F(x)) :=
D = {am=1},
T = GetT(m, s),
// для каждого уравнения
for (j = 1, j `!=` #T + 1, j++ ) do
Poly = { },
// получаем моном и решаем уравнение
for ( L = First(m,s,Tj), L `!=` null, L = Next(m,s,Tj) ) do
P = GetPartition(L), // получаем разбиение P числа Tj
M = GetMonom(P), // получаем моном M для Tj, k
Poly = Poly + M, // добавляем моном M в полином Poly
// получаем уравнение Eq,
// подставляем в него значения известных коэффициентов из D
Eq = GetEquation(Poly)
end
S = Solve(Eq), // получаем решение S линейного уравнения Eq
D = D + S // добавляем S в список D
end
|
Рис. 1 – Алгоритм декомпозиции полиномов, основанный на разбиениях
Алгоритм работает следующим образом. В список известных коэффициентов D записываем заданное значение коэффициента am, то есть D = {am=1}. Формируем список номеров уравнений T функцией GetT. Затем для каждого уравнения из списка T генерируется список разбиений P, по P получается список мономов M. Далее из мономов составляется уравнение Eq и находится его решение S. Найденные коэффициенты добавляются в список известных коэффициентов D. Пример работы алгоритма Пусть дан полином` `
`F(x)=2x^12-6x^11-6x^10+28x^9+3x^8-48x^7+5x^6+36x^5-5x^4-11x^3+x^2+x,`
при этом ` t = 12. ` Представим `F(x)` композицией полиномов `B(A(x))` при `m=4` и `s=3` (`m` и `s` — степени полиномов `A(x)` и` B(x)` соответственно).
Список `D={a_4=1}`.
Функция GetT формирует список номеров уравнений `T={ 12, 11, 10, 9, 8, 1 }`. Рассмотрим конкретные типичные итерации работы алгоритма.
Итерация цикла для `j = 1`, при этом `T_1=12`. Получаем разбиение `P = { 4, 4, 4 }`. По разбиению `P` с помощью функции GetMonom получаем моном `((3),(3))a_4^3 b_3` , затем — уравнение `a_4^3 b_3=f_12`. Подставив известные коэффициенты `a_4=1` и `f_12=2`, получаем уравнение `b_3=2`. Список известных коэффициентов `D={ a_4=1, b_3=2 }`.
Итерация для `j=2`, при этом `T_2=11`, разбиение `P={ 3, 4, 4 }.` По разбиению `P` получаем моном `((3),(1)) ((2),(2))a_3^1 a_4^2 b_3`, затем — уравнение `3a_3a_4^2 b_3=f_11`. Подставив известные коэффициенты `D= {a_4=1, b_3=2 }` и `f_11=-6`, получаем уравнение `6a_3=-6`. Список известных коэффициентов `D={ a_4=1, b_3=2, a_3=-1 }`.
Итерация для `j=5`, `T_5=8`. Получаем первое разбиение `P={ 0, 4, 4 }`. По разбиению `P`получаем моном`((2),(2)) a_4^2 b_2` . Получаем второе разбиение `P={ 1, 3, 4 }`. По разбиению `P` получаем моном `((3),(1)) ((2),(1)) ((1),(1)) a_1^1a_3^1a_4^1b_3`. Получаем третье разбиение`P={ 2, 2, 4 }`. По разбиению `P` получаем моном `((3),(2)) ((1),(1)) a_2^2a_4^1b_3`. Получаем четвертое разбиение `P={ 2, 3, 3 }`. По разбиению `P`получаем моном
`((3),(1)) ((2),(2)) a_2^1 a_3^2 b_3`. Получаем уравнение из всех мономов `a_4^2b_2+6a_1a_3a_4^1b_3+3a_2^2a_4b_3+3a_2a_3^2 b_3=f_8`. Подставив известные коэффициенты`D={ a_4=1, b_3=2, a_3=-1, a_2=-2, a_1=1 }`и `f_8=3`, получим уравнение `b_2-12+24-12=3`. Список известных коэффициентов
`D={ a_4=1, b_3=2, a_3=-1, a_2=-2,a_1=1, b_2=3 }`.
Получение и решение остальных уравнений аналогично. Таким образом, находим все коэффициенты полиномов композиции —`{a_4=1, b_3=2, a_3=-1,a_2=-2,a_1=1,b_2=3,b_1=1 }`. Тогда искомые полиномы `A(x)` и `B(x)` будут иметь вид:
`A(x)=x-2x^2-x^3+x^4,quad B(x)=x+3x^2+2x^3.` Исследование алгоритма Определим вычислительную сложность `z(n)` рассмотренного алгоритма GetDecomposition. В соответствии с алгоритмом для каждого уравнения из списка `T` генерируется список разбиений `P`, по `P`получается список мономов `M`. Далее из мономов составляется уравнение `Eq` и находится его решение `S`.
Таким образом, `z(n)` состоит из нескольких частей, каждая из которых рассматривается далее.
1. Временная сложность генерации разбиений.
В работе [11] приведена временная сложность алгоритма разбиения числа `n` на `s` частей. Там же Д. Кнут ввел обозначение числа разбиений `n` не более чем на `s` частей как `|[n],[s]|` . В отличие от разбиений Кнута, авторами рассматриваются разбиения, у которых ограничены еще и сами части. Взяв за основу обозначение Д. Кнута, в данной работе используется расширенное обозначение `|[n],[[m,s]]|` — число разбиений `n` не более чем на `s` частей, каждая из которых не превосходит `m`.
В обозначениях, введенных в данной статье, временная сложность алгоритма разбиения числа `n` на `s` частей имеет вид
![f(s,n)=3 |[n],[s]|+s,](http://www.e-notabene.ru/mimetex.php?%5Cdisplaystyle%7Bf%7B%7B%5Cleft(%7Bs%7D%2C%7Bn%7D%5Cright)%7D%7D%7D%3D%7B3%7D%7B%5Cleft%7C%5Cmatrix%7B%7Bn%7D%5C%5C%7Bs%7D%7D%5Cright%7C%7D%2B%7Bs%7D%2C)
где `|[n],[s]|` — число операций для подсчета числа разбиений натурального числа `n`, количество частей которых не превышает `s`.
Данная временная сложность `f(s,n)` будет выше, чем временная сложность для генерации ограниченных разбиений, рассматриваемых в данной статье, так как ещё сами части разбиения ограничены числом `m`. Поэтому примем `f(s,n)` в качестве верхней границы для `z_1(m,s,n) = 3|[n],[[m,s]]| + s` — временной сложности генерации ограниченных разбиений числа `n`, каждая часть которых не превышает `m` и число частей не больше `s`.
2. Временная сложность получения монома.
В исследуемом алгоритме моном строится по разбиению, поэтому временная сложность получения мономов складывается из временной сложности генерации разбиений. Длина одного разбиения равняется `s` . Таким образом, получим временную сложность получения монома `z_2(m,s,n)=s |[n],[[m,s]]|.`
3. Временная сложность решения уравнения.
Временная сложность решения уравнения определяется числом подстановок известных коэффициентов из списка `D` в `(m+s-1)` уравнений:
`z_3(m,s)=frac{(m+s-1)(m+s)}{2}.`
Таким образом, временная сложность в п. 1 и п. 2 рассмотрена только для одного уравнения. Учитывая временную сложность для всех уравнений, число которых равняется `m+s-1` , получим `z(m,s)`:
`z(m,s)=z_1(m,s,n)+z_2(m,s,n)+z_3(m,s)= sum_(j=1)^(m+s-1) ( 3 |[n],[[m, s]]| + s + s | [n], [[m, s]]|) + frac{(m+s-1)(m+s)}{2}.`
Предположим, что `m approx s`. Введем обозначение `q(n)=|~ sqrt{n}~|` при условии `sm=n`. Таким образом, `m approx s approx q(n)`. Произведем замену при расчете временной сложности алгоритма декомпозиции:
`z(n)=sum_(j=1)^(2q(n)-1) (3 |[n],[[q(n),q(n)]]| + q(n) + q(n) |[n],[[q(n),q(n)]]| ) + frac{(2q(n)-1)(2q(n))}{2}.`
Упростим полученное выражение:
`z(n)=sum_(j=1)^(2q(n)-1) ( 3 |[n],[[q(n),q(n)]]| +q(n)+q(n) |[n],[[q(n),q(n)]]| )+q(n)cdot (2q(n)-1)= (3+q(n)) sum_(j=1)^(2q(n)-1) (|[n],[[q(n),q(n)]]| )+2q(n)cdot (2q(n)-1).`
Рассмотрим временную сложность алгоритма генерации числа разбиений, когда `|[n/2],[[q(n), q(n)]]|`, то есть когда для нахождения решения берутся уравнения с номерами `i approx t/2`(самые сложные и длинные).
В энциклопедии OEIS представлена приблизительная формула для нахождения числа разбиений `|[n^2/2],[[n,n]]|`, имеющая ошибку около 0.0001% [12]:
`|[n^2/2],[[n,n]]| approx frac{sqrt{3}}{pi} cdot frac{4^n}{n^2+frac{3n}{5}+frac{1}{5}}.`
Применим данную формулу для рассматриваемой временной сложности генерации разбиений:
`|[n/2],[[q(n),q(n)]]| approx frac{sqrt{3}}{pi} cdot frac{4^{q(n)}}{n+frac{3q(n)}{5}+frac{1}{5}}.`
Таким образом, получено, что при решении уравнений с номерами `i approx t/2`, алгоритм генерации разбиений будет иметь экспоненциальную сложность, так как `|[n/2],[[q(n),q(n)]]|` имеет в числителе экспоненциальную функцию `4^{q(n)}`, а в знаменателе — полином. Но `m approx s approx q(n)`, поэтому в нашем случае решаются уравнения с номерами `1 le i le s-1` и `t-m le i le t`. Поэтому необходимо найти временную сложность генерации разбиений для данных уравнений.
1. Первые `s-1`уравнений будут иметь номера 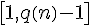 : :
`|[q(n)],[[q(n),q(n)]]| = 1.`
2. Последние `m`уравнений будут иметь номера `[n-q(n), n]`:
`|[n-q(n)],[[q(n),q(n)]]| le n.`
Таким образом, `z(n)=( 3n+nq(n) ) ( 2q(n)-1 )+4n-2q(n)=(5n-2)q(n)+n+2n^2`, то есть вычислительная сложность `z(n)=O (n^2)`.
Сравним вычислительную сложность представленного алгоритма с его аналогами.
Алгоритм декомпозиции полиномов Д. Р. Бартона и Р. Е. Зиппель [4] имеет вычислительную сложность `O (n^2)`. Упрощенная версия этих алгоритмов, представленная Алагар и Тан в работе [5], имеет вычислительную сложность того же порядка, что и у их предшественников. Алгоритм декомпозиции полиномов Д. Козен и С. Ландау [6] имеет вычислительную сложность `O (n^2)`. Алгоритм декомпозиции полиномов Джун-Кюн Сон, Мен-Су Ким и Г. Элбера [7] состоит из нескольких частей. Время работы алгоритма нахождения внутреннего полинома композиции составляет `O(kn)`, а алгоритма нахождения внешнего полинома композиции — `O (n^2)`, где `n`— степень полинома композиции. Вычислительная сложность общего алгоритма равна `O (n^3)`, так как алгоритм нахождения внешнего полинома содержит в себе алгоритм поиска внутреннего полинома.
Анализ показал, что большинство алгоритмов декомпозиции полиномов имеют вычислительную сложность `O (n^2)`.
В работе [7] говорится о том, что для практических целей используются полиномы, представленные композицией, степень которых не превышает 30. На рисунке 2 приведено наглядное сравнение вычислительных сложностей алгоритма декомпозиции полиномов, основанного на разбиениях, с его аналогами при `n le 30`.
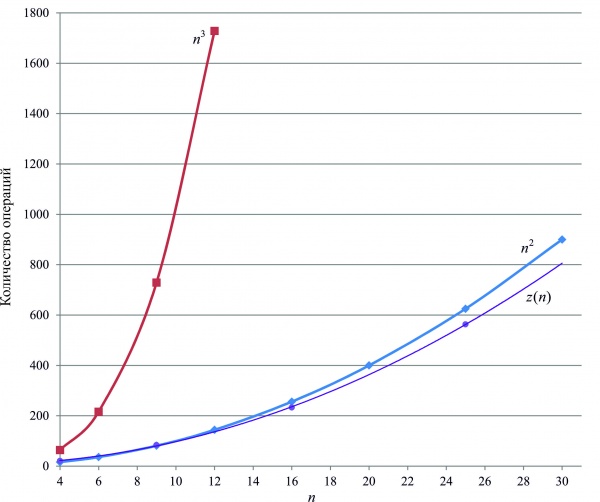
Рис. 2 – Анализ алгоритмов декомпозиции полиномов
На рисунке 2 график `z(n)`построен на экспериментальных данных. Алгоритм запускался с исходными данными `m=s`, `mlts` и `mgts` (при этом разница между `m` и `s` равна 1). При каждом запуске считалось число операций, которые выполняет алгоритм для нахождения полиномов композиции.
Предложенный алгоритм имеет вычислительную сложность `O(n^2)` в лучшем случае, то есть когда `m=s`. Если рассмотреть алгоритм в худшем случае, когда решаются уравнения с номерами близкими к `t/2` (`m`  `s`), то он будет иметь экспоненциальную временную сложность. Рассмотренные аналоги алгоритма декомпозиции полинома не были исследованы авторами в худших случаях, поэтому по ним сложно сделать какие-либо выводы. `s`), то он будет иметь экспоненциальную временную сложность. Рассмотренные аналоги алгоритма декомпозиции полинома не были исследованы авторами в худших случаях, поэтому по ним сложно сделать какие-либо выводы. Заключение Представлен оригинальный алгоритм нахождения декомпозиции полинома. Рассмотрена его вычислительная сложность. Показано, что вычислительная сложность сопоставима с известными алгоритмами.
Библиография
1. Бухбергер Б., Калме Ж., Калтофен Э. и др. Компьютерная алгебра. Символьные и алгебраические вычисления / пер. с англ. М.: Мир, 1986. 392 с.
2. Мысовских В. И. Системы компьютерной алгебры и символьные вычисления // Записки научных семинаров ПОМИ РАН. 2001. Т. 281. С. 227–236.
3. Кулябов Д. С., Кокотчикова М. Г. Аналитический обзор систем символьных вычислений // Вестник РУДН, серия «Математика. Информатика. Физика». 2007. № 1-2. С. 38–45.
4. Barton D. R., Zippel R. E. Polynomial decomposition algorithms // Journal of Symbolic Computation. 1985. Vol. 1. No. 2. Pp. 159–168.
5. Alagar V. S., Thanh M. Fast polynomial decomposition algorithms // Proceedings of European Conference on Computer Algebra. 1985. Pp. 150–153.
6. Kozen D., Landau S. Polynomial decomposition algorithms // Journal of Symbolic Computation. 1989. No. 7. Pp. 445–456.
7. Seong J.-K., Elber G., Kim M.-S. Polynomial Decomposition and Its Applications. 2003. 12 p. URL: http://www.cs.utah.edu/~seong/decomposition.pdf (дата обращения: 09.07.2015).
8. Кручинин В.В., Кручинин Д.В. Степени производящих функций и их применение. Томск: ТУСУР, 2013. 234 с.
9. Перминова М. Ю., Кручинин В. В. Алгоритмы рекурсивной генерации ограниченных разбиений натурального числа // Доклады Томского государственного университета систем управления и радиоэлектроники. №4(34), 2014. Стр. 89–94.
10. Перминова М. Ю., Кручинин В. В. Алгоритм декомпозиции полиномов, основанный на разбиениях // Доклады Томского государственного университета систем управления и радиоэлектроники. №4(38), 2015 [в печати].
11. Кнут Д. Искусство программирования / пер. с англ. М.: ООО «И. Д. Вильямс», 2007. Т. 4, вып. 3. 208 с.
12. OEIS — онлайн-энциклопедия целочисленных последовательностей. URL: https://oeis.org/A029895 (дата обращения: 03.08.2015).
References
1. Bukhberger B., Kalme Zh., Kaltofen E. i dr. Komp'yuternaya algebra. Simvol'nye i algebraicheskie vychisleniya / per. s angl. M.: Mir, 1986. 392 s.
2. Mysovskikh V. I. Sistemy komp'yuternoi algebry i simvol'nye vychisleniya // Zapiski nauchnykh seminarov POMI RAN. 2001. T. 281. S. 227–236.
3. Kulyabov D. S., Kokotchikova M. G. Analiticheskii obzor sistem simvol'nykh vychislenii // Vestnik RUDN, seriya «Matematika. Informatika. Fizika». 2007. № 1-2. S. 38–45.
4. Barton D. R., Zippel R. E. Polynomial decomposition algorithms // Journal of Symbolic Computation. 1985. Vol. 1. No. 2. Pp. 159–168.
5. Alagar V. S., Thanh M. Fast polynomial decomposition algorithms // Proceedings of European Conference on Computer Algebra. 1985. Pp. 150–153.
6. Kozen D., Landau S. Polynomial decomposition algorithms // Journal of Symbolic Computation. 1989. No. 7. Pp. 445–456.
7. Seong J.-K., Elber G., Kim M.-S. Polynomial Decomposition and Its Applications. 2003. 12 p. URL: http://www.cs.utah.edu/~seong/decomposition.pdf (data obrashcheniya: 09.07.2015).
8. Kruchinin V.V., Kruchinin D.V. Stepeni proizvodyashchikh funktsii i ikh primenenie. Tomsk: TUSUR, 2013. 234 s.
9. Perminova M. Yu., Kruchinin V. V. Algoritmy rekursivnoi generatsii ogranichennykh razbienii natural'nogo chisla // Doklady Tomskogo gosudarstvennogo universiteta sistem upravleniya i radioelektroniki. №4(34), 2014. Str. 89–94.
10. Perminova M. Yu., Kruchinin V. V. Algoritm dekompozitsii polinomov, osnovannyi na razbieniyakh // Doklady Tomskogo gosudarstvennogo universiteta sistem upravleniya i radioelektroniki. №4(38), 2015 [v pechati].
11. Knut D. Iskusstvo programmirovaniya / per. s angl. M.: OOO «I. D. Vil'yams», 2007. T. 4, vyp. 3. 208 s.
12. OEIS — onlain-entsiklopediya tselochislennykh posledovatel'nostei. URL: https://oeis.org/A029895 (data obrashcheniya: 03.08.2015).
Ссылка на эту статью
Просто выделите и скопируйте ссылку на эту статью в буфер обмена. Вы можете также
попробовать найти похожие
статьи
|
|





