|
ГЛАВНАЯ
> Вернуться к содержанию
Электроника и электротехника
Правильная ссылка на статью:
Белозеров В.В.
О вероятностно-физическом подходе к вопросу надежности и безопасности изделий электронной техники
// Электроника и электротехника.
2018. № 3.
С. 17-50.
DOI: 10.7256/2453-8884.2018.3.27552 URL: https://nbpublish.com/library_read_article.php?id=27552
О вероятностно-физическом подходе к вопросу надежности и безопасности изделий электронной техники
Белозеров Валерий Владимирович
доктор технических наук
профессор, Донской государственный технический университет, Генеральный директор, ООО "НПТ Центр ОКТАЭДР"
344091, Россия, Ростовская область, г. Ростов-на-Дону, ул. Каширская, 22
Belozerov Valerii Vladimirovich
Doctor of Technical Science
General Director at LLC “Scientific Technological Production Center OKTAEDR”; Professor at the department of Automation of Production Processes, Don State Technical University
344091, Russia, Rostov-on-Don, ul. Kashirskaya, 22-41

|
safeting@mail.ru
|
|
 |
Другие публикации этого автора
|
|
|
DOI: 10.7256/2453-8884.2018.3.27552
Дата направления статьи в редакцию:
01-10-2018
Дата публикации:
10-11-2018
Аннотация:
В статье представлены результаты разработки эффективных методов испытаний и диагностики изделий электронной техники (ИЭТ), радиоэлектронной аппаратуры (РЭА), электротехнического оборудования (ЭТО), электроприборов (ЭП) и средств вычислительной техники (СВТ) в аспектах их качества, надежности и безопасности. В результате системного анализа и последующего системного синтеза предложены вероятностно-физические модели решения проблем надежности и безопасности с помощью технологии ускоренного технологического прогона ЭП и СВТ, который с помощью модулей термоэлектронной защиты позволяет за счет электро-термо-циклирования осуществить тепловую локацию комплектующих его электрорадиоэлементов (ЭРЭ), и обнаружить отклонения от расчетных коэффициентов нагрузки, что позволяет вычислить надежность и пожаробезопасный ресурс каждого изделия. Использована методология обнаружения пожароопасных отказов ЭРЭ в ЭП и СВТ по лавинному росту температуры с последующим отключением электроприбора от сети, с предотвращением, таким образом, его загорания. Новизна предлагаемого подхода заключается в возможности периодической диагностики наработки на отказ (в рамках гарантийного обслуживания изделий), для своевременного вывода РЭА и ЭП из эксплуатации, и предотвращения таким образом социально-экономических потерь от возникающих аварий и пожаров, в следствие несоответствия технического и пожаробезопасного ресурсов.
Ключевые слова:
электрорадиоэлементы, изделия электронной техники, электротехнические приборы, средства вычислительной техники, надежность, безопасность, ускоренные испытания, термоэлектроцикл, технический ресурс, пожаробезопасный ресурс
Abstract: The article presents the results of the development of effective methods of testing and diagnostics of electronic equipment (EE), radio-electronic devices (RED), electrical appliances (EA) and computer equipment (CE) in terms of their quality, reliability and safety.As a result of the system analysis and subsequent system synthesis, probabilistic-physical models for solving reliability and safety problems are proposed using the technology of accelerated technological run of EA and CE, which with the help of thermo-electronic protection modules allows, due to electro-thermo-cycling, to carry out the thermal location of its components of electrical elements (CEE), and to detect deviations from the calculated load factors, which allows to calculate the reliability and fire-safe resource of each product.The methodology of detection of fire-dangerous failures of electrical and radio elements (ERE) in EP and CE on avalanche growth of temperature with the subsequent disconnection of the electric device from a network, with prevention, thus, its ignition is used.The novelty of the proposed approach lies in the possibility of periodic diagnostics of time-to-failure (within the warranty service of products), for the timely withdrawal of RED and CE from operation, and thus prevent socio-economic losses from emerging accidents and fires, as a result of non-compliance of technical and fire-safe resources.
Keywords: electrical and radio elements, electronic equipment, electrical appliance, computer equipment, reliability, safety, accelerated testing, thermo-electric cycle, technical resource, fire-safe resource
Введение
Расширение применения информационно-коммуникационных технологий (ИКТ) и изделий электронной техники (ИЭТ) в науке, технике и в быту, обострили проблемы разработки и применения новых и эффективных методов испытаний и диагностики электрорадиоэлементов (ЭРЭ) в радиоэлектронных и электротехнических приборах, на предмет обеспечения их надежности и безопасности.
В настоящее время в науке и практике общепринятыми способами оценки качества, надежности и безопасности ИЭТ в радиоэлектронной аппаратуре (РЭА) и электроприборах (ЭП) являются статистические методы [1-4]. Все международные и национальные стандарты используют для этих целей, как правило, экспоненциальные распределения, несмотря на то, что научно обоснована необходимость применения, как других видов статистических распределений [5,6], так и термодинамического подхода [7,8], что влечет за собой недостоверные данные о качестве, надежности, долговечности и безопасности ИЭТ, РЭА и ЭП [9-11].
Представляя КАЧЕСТВО [12], как свойство безопасной работы объекта (ИЭТ, РЭА, ЭП) во времени, т.е. как долговечность и надежность с минимальным «общественным вредом» (с минимальными материальными и моральными потерями при эксплуатации), в Ростовском государственном университете была разработана «Концепция общей безопасности» [11] и на протяжении многих лет разрабатывались отдельные модели вероятностно-физической методологии оценки надежности, долговечности и безопасности объектов и процессов, в том числе ИЭТ, РЭА и ЭП [8-13] - как основы количественного метода квалиметрии.
Проблемы надежности и долговечности РЭА и ЭП, связаны с процессами старения и деградации свойств полупроводников, диэлектриков и проводников, используемых в них, и решаются на основе определения их физико-химических состояний, и связаны с основным понятием надежности - отказом, событием, заключающимся в нарушении работоспособности изделия [1,4,12].
Определение физической природы отказов, их причин и корректное математическое описание явлений, лежащих в их основе, являются необходимыми условиями решения всех практических задач надежности. Именно поэтому правильный выбор теоретических моделей, описывающих отказы высоконадежных элементов, в частности, микросхем, транзисторов, конденсаторов, резисторов и других ЭРЭ, которые используются в РЭА и ЭП, является сложной задачей, так как в отличие от моделей отказов для слабо надежных элементов, например, механических объектов, для ЭРЭ невозможно получить данные отказов всех поставленных на испытание элементов [5,6].
Следствием деградации физико-химических свойств материалов, из которых состоят ЭРЭ, является их опасность для человека и окружающей его среды, с точки зрения диссипации запасенной или преобразуемой ими энергии, что при отказе (помимо потери работоспособности) может привести к пожару, взрыву и другим опасным факторам [12].
В последнее время все более отклоняется общепринятое деление отказов ЭРЭ в РЭА и ЭП на "внезапные" и "постепенные", что приводило к недостоверному выбору вероятностных моделей отказов [6-12].
До настоящего времени отказ считается "внезапным", если не установлена его причина и подразумевается, что отказ появился в результате мгновенного изменения какого-то параметра, чем практически отрицается существование каких-либо физических деградационных процессов - настоящих причин, приведших к отказу. При этом оказывалось, что отказ идентифицировался как "внезапный" лишь потому, что в тот момент не было средств контроля изменения всех определяющих параметров, способных его вызвать [12].
Установленные физические модели отказов многих ЭРЭ описаны довольно подробно [1,5-9], основными из которых являются: механические разрушения, интерметаллизация, электромиграция, теплоэлектрический пробой, генерация и перемещение зарядов на поверхности кристаллов, коррозия, плавление, образование поверхностных плёнок, старение материалов [12].
Таким образом, физическая природа "внезапных" (с неизвестной причиной) и "постепенных" (с известной причиной) отказов одна и та же - это результат деградационных процессов в материалах ЭРЭ, из которых собраны, РЭА и ЭП во время их испытаний, хранения и эксплуатации. Только во «внезапных случаях» процессы деградации протекают очень быстро, что приводит к отказам и к скачкообразным изменениям контролируемых параметров, и факт возникновения отказа представляется неожиданным для исследователя. В «постепенных случаях», определяющие параметры, изменения которых и вызвали отказ, контролируются, и достижение их предельных значений не является неожиданным.
Вероятностно-физическая модель надежности изделий
Вероятностно-физическая модель отказа включает в себя определение «текущих» интенсивностей отказов элементов изделий по модифицированному уравнению Аррениуса-Эйринга [13]:
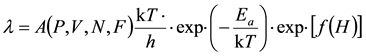 (1) (1)
где λ - текущая интенсивность отказа элемента, 1/час; А=ki∙λО –произведение безразмерных коэффициентов, зависящих от давления, влажности, вибраций и т.д.) на интенсивность отказов при хранении (λО), 1/час; k - постоянная Больцмана, 1.38·10-23 Дж/К; Т - температура элемента, ºК; h - постоянная Планка, 6.626·10-34 Дж·с; Ea- эффективная энергия активации отказа, Дж; f(H)- функция нетермической (энергетической) нагрузки.
До настоящего времени это уравнение (1) не удавалось решить (для каждого ЭРЭ в РЭА и ЭП) по трем причинам [14]:
методологическим – определение энергии активации отказа даже для одного ЭРЭ оказывалось практически не разрешимой задачей, так как приходилось выбирать превалирующий процесс деградации (термодиффузия, электромиграция, коррозия и т.д.), т.е. не измерять, а подбирать её значение;
метрологическим - точное измерение параметров окружающей ЭРЭ среды, его температуры и энергетической нагрузки было не возможно, из-за внесения самими средствами измерения (СИ) изменений и потерь в процессы электро-тепло-массобмена;
технико-экономическим – количества ЭРЭ в РЭА и ЭП измеряются десятками, сотнями и тысячами, поэтому на каждый элемент СИ не поставить.
Решение было найдено [15,16] путем термозондирования окружающего воздуха [TВОЗД(t)] и внутреннего объема РЭА или ЭП [T(t)], а также измерением потребляемой изделием энергии [E(t)], при известных минимальных (λmin), номинальных (λном) и максимальных (λмах) значениях интенсивности отказов всех элементов. Единственным допущением считалось то, что все элементы расположены на платах, установленных регулярно (вертикально или горизонтально с определенным шагом), у каждой из которых также измеряется потребляемая энергия [Wp(t)], тогда решением уравнений теплового баланса и Навье-Стокса (прямая и обратная задачи тепловой локации), определялись все текущие коэффициенты энергетических нагрузок элементов [EL(t)]:
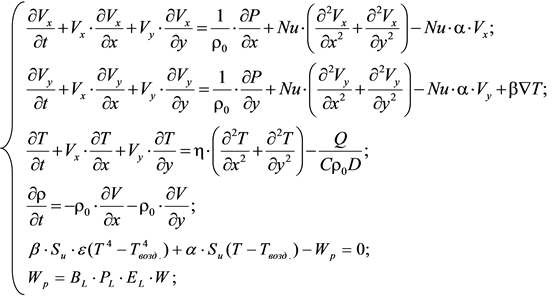 (2) (2)
где α, β, ρ, η - коэффициенты, Nu- число Нуссельта; С - теплоемкость, D- расстояние, σ - постоянная Стефана- Больцмана, Sи - площадь поверхности источника тепла (ЭРЭ), WP - потребляемая источником тепла мощность (фактическая), ТВОЗД. - температура окружающего источник тепла воздуха/зонда, Т - искомая/измеренная температура источника тепла (ЭРЭ, платы, стенки и т.д.), BL - коэффициент энергетической нагрузки конструктива (блока,изделия), PL - коэффициент энергетической нагрузки платы (модуля), W - номинальная (паспортная) потребляемая мощность, ЕL - коэффициент энергетической нагрузки ЭРЭ (микросхемы, резистора и т.п.).
Определение коэффициентов энергетической нагрузки по указанному уравнению (1), превращало λ в функцию, у которой для любого ЭРЭ известны минимальное (λО), номинальное (λном), максимальное (λмах) значения интенсивности отказов, а также интенсивность отказов при хранении (λх), что позволяло построить и аппроксимировать «семейство» λ-кривых в плоскость, ограниченную кривыми λх(Т) и λмах(Т). Далее, логарифмированием получалась функция эффективной энергии активации отказов каждого ЭРЭ - Еai(Н,Т).
Далее, подставляя в уравнения (1) текущие значения функций энергетических нагрузок каждого ЭРЭ, текущие значения температур их корпусов, текущие значения функций эффективной энергии активации отказа им соответствующие, а также текущие значения параметров окружающей среды (давления, влажности, вибрации и т.д.),получаем текущие интенсивности отказов ЭРЭ , т.е. функции λ (Н,Т,Р), которые нельзя описывать экспоненциальными распределениями [10-16].
Именно с помощью термозондирования тепловых потоков от ЭРЭ позисторами, на которые был получен Патент РФ № 2060566 от 20.05.96 [17], удалось устранить ограничения, возникающие при решении системы уравнений (2) в двумерном приближении Обербека-Бусcинеска в «прямой и обратной задачах» тепловой локации элементов, чтобы получить значения функции нетермической нагрузки f(H) [18].
Как показали исследования [10-18], полученные функции интенсивности отказов можно описывать γ-распределениями [10]. При этом нахождение параметров γ-распределения случайной величины λi в данном случае сводилось к задаче определения параметров В и С функции γ-распределения по заданному двустороннему 100% доверительному интервалу
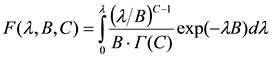 при В>0,С>0,5,Г(С)-гамма-функция (3) при В>0,С>0,5,Г(С)-гамма-функция (3)
т.е. по заданным ее квантилям λн = λmin и λв = λмах уровней вероятности соответственно L и 1-L, где L=(1-р)/2, к решению системы уравнений:
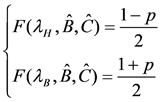 (4) (4)
с последующей заменой переменной х = 2λ/В, переводящей γ- распределение в обобщенное χ2 – распределение (для снятия ограничений относительно целочислености v), после чего делением одного уравнения на другое находится:
q (v) = λв / λн (5)
Полученные значения q (v) = χ21-L(v)/ χ2L(v) являются монотонной функцией от v, имеющей при λв/λн>О единственный корень, а по вычисленному v(а следовательно, и С= v/2), находится и второй параметр γ-распределения:
В = 2λн/χ2L(v) = 2 λв/χ2 1-L(v). (6)
Для реализации стендовых испытаний РЭА и ЭП по разработанной методологии, необходимо было рассчитать режим корректного ускорения испытаний, т.е. найти коэффициент ускорения КУ , равный [10-13]:
КУ = КНТЦ ∙ КВ , (7)
где КВ - коэффициент учета внешней среды (влажности, давления, вибраций и т.п.), кроме температуры и электрической нагрузки;
КНТЦ - коэффициент (функция) учета совместного влияния на λ: электрической нагрузки, температуры окружающей ЭРЭ среды и параметров циклирования (включения и выключения ЭРЭ).
Сопоставляя уравнения (1 и 7), найдем выражение для КУ[13]:
КУ = КВ∙КНЦ ∙КТ, (8)
где КВ = А(P,V,W,N) – коэффициент (функция) учета внешней среды, независящий от изменения электрической нагрузки и слабо коррелирующий с изменениями температуры;
КТ = kT·exp(-Ea/kT) - коэффициент (функция) учета влияния температуры, независящий от изменений внешней среды и слабо коррелирующий с изменениями электрической нагрузки;
КНЦ = exp[f(H)]/h - коэффициент (функция) учета влияния электрической нагрузки, независящий от изменений внешней среды и слабо коррелирующий с изменениями температуры, характеризуемый функцией нагрузки f(Н), рекомендуемыми значениями которой являются значения равные 0,2–0,9 от – номинальных, при этом f(Н)=0 в цикле «выключения», а непрерывный режим работы является частным случаем при частоте цикла равной 0.
Функция учета влияния электрической нагрузки f(Н) определяется как отношение заданной рабочей нагрузки WРАБ к нагрузке WНОМ номинального режима [5,6,13]:
f(Н) = WРАБ / WНОМ ,
где в качестве нагрузки W для ЭРЭ обычно выступают - мощность (для транзисторов, резисторов, микросхем), - напряжение (для конденсаторов, разъемов), - сила тока (для диодов, выключателей), - плотность тока в обмотке (для трансформаторов, дросселей).
При определении указанных нагрузок могут применяться и другие параметры режима (скважность сигналов, отношения сигналов верхнего и нижнего уровня к - номинальному и т.д.), однако во всех случаях f(Н) выражает нагрузку в долях от номинальной и является безразмерной.
Пренебрегая корреляцией КB с температурой, коэффициент ускорения КУ был определен без КB как КНТЦ, и найден из условия [13]:
λ·t = λР·tР + λЦ·v·t + λОЖ·tОЖ ,
где, в соответствии с вышеприведенными уравнениями предполагалось, что
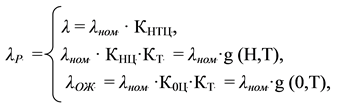
(9)
при t- общее полезное время испытаний в часах, в котором не учитываются задержки на восстановления изделий после отказов;
tР =r·t - суммарное время нахождения изделия во включенном (рабочем) состоянии в процессе испытаний, а r - доля tР в t ;
v - частота циклирования (или средняя частота, если регулярность циклирования нарушается), 1/час.;
tОЖ = t - tР = (1 - r) · t - суммарное время нахождения изделия в выключенном состоянии в процессе испытаний (т.е. в состоянии ожидания включения) при средней продолжительности:
t Ц.Р = r/v - рабочей стадии цикла, час.,
t Ц.ОЖ = (1-r)/v - нерабочей стадии цикла, час.,
λР - интенсивность отказов элемента во включенном состоянии при средней температуре ТР рабочего состояния:
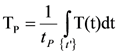 (10) (10)
где Т(t)- температура окружающей среды для элемента как функция времени t;
{t }- совокупность интервалов времени пребывания изделия во включенном состоянии в рабочих стадиях циклов;
λЦ - интенсивность внезапных отказов элемента, возникающих в момент включения или выключения изделия (на один цикл включения);
λОЖ - интенсивность отказов, возникающих в выключенном элементе при средней температуре ТОЖ ожидания работы:
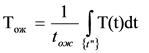 (11) (11)
где {t”} - совокупность интервалов времени пребывания изделия в выключенном состоянии - в нерабочих стадиях циклов;
Итоговое выражение для коэффициента циклирования было получено в виде
КНТЦ = r·g (Н, ТР) + (1 - r) · g (0, ТОЖ) + q·v , (12)
где q = λЦ / λном
Совмещая испытания на функционирование и надежность, и подбирая план испытаний РЭА и ЭП (диапазоны режима «термо-баро-электро-циклирования»), можно контролировать «обратимые» и «необратимые» процессы в ЭРЭ, в т. ч. по модифицированной формуле Аррениуса-Эйринга, где SO - энтропия отказа [12]:
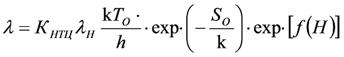 (13) (13)
Таким образом, получаем возможность продуктивно использовать экспериментальный этап, во-первых, для уточнения интенсивностей отказов λмин и λном (в режиме хранения и номинальном режиме), если баро-термо-электро-цикл «охватывает» интервал интенсивностей отказов от хранения ЭРЭ до номинального режима, а во-вторых, для получения значений функции производства энтропии - ∆S, логарифмируя «соседние» значения λ-функции и вычисляя их разность [13].
Вероятностная физико-химическая модель
Разработанные модели и методология БЭТА-анализа физико-химических свойств материалов позволили начать решение проблемы количественного определения параметров ЭРЭ, РЭА и ЭП, обуславливающих их эксплуатационную устойчивость и пожарную опасность, а также по аналогии с долговечностью (техническим ресурсом) ввести понятие пожаробезопасного ресурса, который рассчитывается по термодинамическим и вероятностно-физическим моделям [16].
Была найдена функция распределения вероятностей FЭ (Q) возможных дополнительных тепловыделений Q в элементе Э при условии его отказа [12]:
FЭ(Q) = 1 - vЭ · [1 - GЭ(z)], (Q > 0), (14)
где vЭ - доля пожароопасных отказов среди всех отказов элементов данного типа в рассматриваемых условиях;
GЭ(z)- условная функция распределения (при возникновении пожароопасного отказа) случайной величины z = lg Q ЭРЭ.
Случайная величина Q рассматривается как функция случайных аргументов I и t (R и t), исходя из общего выражения для "Джоулева тепла":
Q = k · U · I · t = k · U2 · t /R, (15)
где I, R - случайные, усредненные за время t значения силы тока и сопротивления в ЭРЭ;
U - рабочее напряжение на ЭРЭ;
k - коэффициент пересчета электрической мощности в тепло, с учетом режима работы ЭРЭ.
Для случайных величин lg I= lg U - lg R, lg t, lg R - принимались нормальные распределения и учитывались их коэффициенты корреляции r, что хорошо согласуется с полученными экспериментальными данными [10,13], вследствие чего функция F(Q) берется для вычислений в следующем виде:
FЭ (Q) = 1 - vЭ + vЭ · Ф [(z -Мz)/ δz (16)
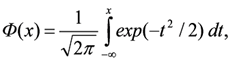 - стандартная ф-ция нормального распределения - стандартная ф-ция нормального распределения
МZ - математическое ожидание случайной величины z= lg Q;
δZ - среднеквадратическое отклонение величины z;
Флуктуациями параметров распределений величин U, I, R в моделях пожароопасных отказов, влияющими на параметры МZ и δZ , пренебрегаем, считая, что уже имеем их усредненные данные по быстротекущим процессам пробоев, коротких замыканий и т.п.
Случайная величина z = lgQ (для удобства применения имеющихся данных при оценке параметров мz и δz) представлена в формуле (14) двумя выражениями (15).
В первом случае имеем [10]:
Q = kU2t/R,
где k и U - постоянные.
Относительно случайных величин х = lgt и у = lgR предполагается, что они имеют совместное двумерное нормальное распределение, определяемое параметрами м1, м2, δ1, δ2, r, где м1, м2 - математические ожидания величин х и у; δ1, δ2 - их дисперсии; r – коэффициент корреляции между х и у. При этом плотность вероятности P (х,у) совместного распределения х и у имеет вид:
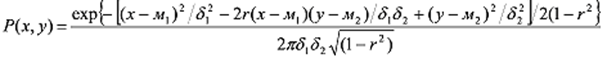 , ,
а частные распределения случайных величин х и у - нормальные с параметрами м1, δ1 и м2, δ2, оценки которых считаются известными.
Согласно уравнению (16) z = lgQ=c1+ х - у, где с1 = lg(kU2) - постоянная. Отсюда мz = c1 + мx-y, δz = δx-y, но распределение суммы (разности) величин х, у, подчиненных совместно распределению Р (х,у), как известно [11], является нормальным, и окончательно для данного случая (16) в принятых обозначениях имеем[10]:
мz = с1 + м1 - м2,
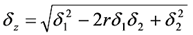 (17) (17)
где с1 = lg(kU2) = lgk + 2lgU.
Во втором случае имеем:
Q = k·U·I·t,
и в предположении совместного нормального распределения величин х=lgt и v=lgI с параметрами м1, м3, δ1, δ3, r* (где м3,δ3 - параметры частного распределения случайной величины v, а r*- коэффициент корреляции между х и v) аналогично предыдущему приходим к выражениям:
z = lgQ = c2 + х + v,
мz = с2 + м1 - м3 , (18)
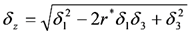
где c2 = lg(kU) = lgk + lgU.
Следует заметить, что при I = U/R имеем V = lgU - у , маргинальные (частные) распределениия v и у оказываются взаимно обусловленными и из нормальности одного вытекает нормальность другого, при простых соотношениях параметров: м3 = lgU - м2, δ3 = δ2, r*= -r. Таким образом, с учетом соотношения c2 = с1 - lgU формулы (18) оказываются эквивалентными формулам (17).
Входящий в выражения (17) коэффициент корреляции r может быть оценен обычными способами в зависимости от характера имеющихся данных: по выборке пар (хi, уi), по группированным данным и т.п.
Оценка r должна согласовываться с линейным среднеквадратическим уравнением регрессии величины у относительно х , которое проходит через точку (м1, м2) и имеет вид
у = м2 + r·δ2/δ1·(х - м1), (19)
или в более симметричном виде,
(у - м2)/δ2 = r·(х - м1)/δ1 , (20)
Теоретический вид функции условного математического ожидания м(ух) является необходимым условием утверждения вида Р (х).
Поэтому все применяемые в (17) оценки 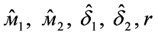 должны согласовываться (с учетом доверительных интервалов) с получаемой по методу наименьшиих квадратов регрессионной прямой вида (20). При этом теоретическое значение остаточной дисперсии равно должны согласовываться (с учетом доверительных интервалов) с получаемой по методу наименьшиих квадратов регрессионной прямой вида (20). При этом теоретическое значение остаточной дисперсии равно
δ2(ух) = δ22·(1-r2)
Для вычисления входящей в выражение (14) Fэ(Q) функции распределения вероятностей нормального закона
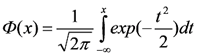
могут быть использованы различные известные аппроксимации.
Таким образом, для оценки пожарной опасности материалов и ЭРЭ из них, разработана модель, в которой тепло пожароопасного отказа ЭРЭ, вычисляемое по логнормальным функциям распределения дополнительного тепловыделения (14), нагревая электрорадиоматериал (ЭРМ), воспламеняет его при переходе процессов деструкции и пиролиза ЭРМ в самоускоряющуюся фазу по критерию Семёнова (Se=0,368), что вполне допустимо, принимая во внимание лавинообразный характер пожароопасного отказа [19]:
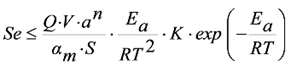 (21) (21)
где Q - тепловыделение пожароопасного события, Дж./сек.; V - объём ЭРМ, м3; S - площадь поверхности ЭРМ, м2; R - газовая постоянная, 8.31441 Дж/моль ·˚К; αm - коэффициент теплоотдачи ЭРМ, Вт/˚К ·м2; Еа - эффективная энергия активации процессов в ЭРМ, Дж/моль; Т - рабочая температура ЭРМ, ˚К; K – предэкспоненциальный множитель, получаемый по результатам термоаналитических испытаний ЭРМ; an- концентрация и порядок реакции в конденсированной фазе.
Одновременно проверяется выполнение условия зажигания каждого соседнего ЭРЭ, при возникновения пожароопасного отказа в - данном, по критическому тепловому потоку Зельдовича [9,10]:
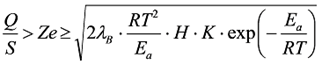 (22) (22)
где Н - тепловой эффект реакций пиролиза и деструкции ЭРМ, Дж./c; λв - теплопроводность газовой фазы, Вт/м·˚К (остальные обозначения переменных, как в уравнении 21).
Численное определение всех параметров обоих неравенств оказывается возможным, если в базе данных есть «образ» - ВФЖЦ материалов, из которых изготовлены ЭРЭ, путем решения следующей системы уравнений в точке воспламенения [20]:
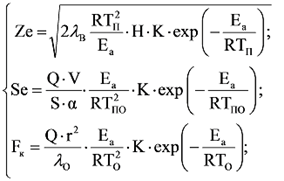 (23) (23)
где Ze – критерий Зельдовича (критическая плотность теплового потока); λв- коэффициент теплопроводности газовой фазы; R - газовая постоянная; Тп - температура печи; Еа - энергия активации пиролиза образца; Н - тепловой эффект реакции в газовой фазе; K - предэкспонент; Se – критерий Семенова (Se=0,368); Q - теплота, подведенная к образцу; V - текущий объём образца; S - текущая площадь поверхности образца; a - текущий коэффициент теплоотдачи образца; Тпо-температура поверхности образца; Fк-критерий Франк-Каменецкого (Fк=2,00); r-линейный размер образца; λо-коэф.теплопроводности образца; То-температура образца.
Расчеты по системе уравнений (23) должны проводиться для каждого ЭРЭ и его «соседей», для чего необходима их топология, а для вероятностной оценки возможности загорания и распространения огня вводится функция «маятник события», формирующая из топологии ЭРЭ в РЭА и ЭП «матрицу загораний» [12]:
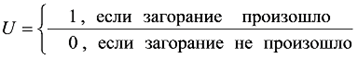
Вероятность развития пожара, т.е. распространения огня (Fр) "на соседа", т.е. распространения загорания «на соседа», формируется с помощью той же функции «маятник события» по неравенству Семенова (21) «для соседа» при критической плотности теплового потока Зельдовича, к которому добавляется дополнительный тепловой поток - ∆Qэ, обусловленный теплотой сгорания (пожаропроизводительностью) воспламенившегося ЭРМ [10,19]:
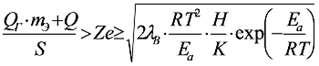 (24) (24)
где QГ - удельная теплота сгорания ЭРМ, Дж/кг; mЭ - горючая масса ЭРМ (убыль массы), кг; S - площадь поверхности ЭРМ, м2;
Математическая модель и алгоритмы, реализующие эти процедуры, позволяют определить [12]:
λПО=λ∙∑vЭ - интенсивности пожароопасных отказов ЭРЭ, как произведение текущей интенсивности отказа (1) на сумму долей пожароопасных отказов (КЗ, пробой, обрыв) в общей статистике их отказов;
λВ=λПО∙FЭ - интенсивности воспламенений элементов, как произведение интенсивности пожароопасных отказов ЭРЭ на вероятность (14) дополнительного тепловыделения - Qэ, достаточного для самовоспламенения ЭРМ по Семенову (21);
Fв=∫λВdλВ - вероятности воспламенений ЭРЭ, как интеграл функции интенсивности их воспламенений;
Fр=F(Qэ +∆Qэ)- вероятность распространения огня, как вероятности дополнительного тепловыделения ЭРЭ и горения ЭРМ, достаточного для «зажигания соседнего ЭРЭ» по Зельдовичу (24);
Fп= Fв ∙Fр - вероятность пожара, как произведение совместных событий – воспламенения по Семенову и распространения по Зельдовичу.
Таким образом, при стендовых испытаниях появляется возможность поверки полученной «матрицы пожара» на соответствие стандарту [2].
Вероятностно-физическая модель электрической опасности изделий
Cуществующие международные стандарты (МЭК) и отечественные стандарты (ГОСТ Р) применяют качественные методы оценки электробезопасности. РЭА и ЭП считаются электробезопасными для потребителя, если в выпускаемых изделиях, установленных на пробойных установках соответствующих напряжений (1 кВ, 2.7кВ, 6кВ и т.д.), пробой не наступает. Очевидно, что такой метод и критерий не позволяют получить вероятностной оценки указанной опасности в зависимости от условий эксплуатации изделий и оборудования (давления, влажности, температуры), чтобы прогнозировать его устойчивость и безопасность, а также не учитывает процессы “старения“, в результате которых изменяется и диэлектрическая проницаемость материалов и другие физические параметры. [11,17].
В данном случае прменение вероятностно-физического подхода заключается в том, что та же логнормальную модель (14) используется в качестве расчетной, где под током в цепи будет подразумеваться ток Таунсендовского разряда, зависящий от давления, напряжения и расстояния пробоя по закону Пашена, с коэффициентами ионизации, определяемыми из уравнения Ленгмюра-Саха [10-12]:
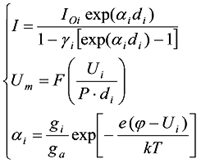 (25) (25)
где I - ток разряда; I0i - плотность тока; α,γ – первый и второй коэффициенты Таунсенда; d – междуэлектродное расстояние; gi,ga– статистические веса ионного и атомного состояний; е – заряд электрона; φ – потенциал выхода; Ui– потенциал ионизации; k – постоянная Больцмана; Р – давление газа; Um - минимальное напряжение пробоя; Т - температура
Аналогично вероятностно-химической модели, через функцию "маятник события" полученный результат "распределяется" по вероятностям последствий пробоя (поражения человека, энергии зажигания и т.п.).
В проведенных исследованиях доказано изменение условий ионизации при наличии высокочастотных полей [10-10,11], что позволяет прогнозировать процессы пробоя на высоких частотах и, как следствие, оценивать электроопасность в блоках и модулях РЭА и ЭП, где практически все электрические напряжения и подводящие их цепи питания сопровождаются электромагнитными колебаниями широкого спектра частот [12].
Термодинамическая модель надежности и безопасности
Применение термодинамического подхода в решении проблем надежности РЭА и ЭП известно давно [7], а вот ие а его использование для решения задач их безопасности разрабатывается сравнительно недавно [8,10], поэтому рассмотрим его использование для объектов различной структуры (изделия, оборудование, здания и т.д.), отметив следующие особенности[12]:
- универсальный характер термодинамических моделей и методов относительно объектов и процессов различной физической природы и сложности;
- кинетический характер термодинамических моделей, отражающих реальные необратимые процессы и явления, включая фактор времени в явном виде;
- свойство аддитивности термодинамических функций и их интегральный характер (в виде интегральной физики дефектов-отказов);
- возможности прямого и косвенного инструментального измерения термодинамических параметров объектов разной степени сложности.
Указанные особенности проявляются и в энергетике взаимодействия объектов с внешней средой (1-й закон термодинамики), и в направленности и динамике необратимого изменения состояния объектов (2-й закон термодинамики). Объединяющим 1-й и 2-й законы термодинамики является уравнение Гиббса [7,8]:
 (26) (26)
или в обобщенной форме:
 (27) (27)
Это выражение представляет типичную структуру термодинамических соотношений, включающих два класса параметров системы:
интенсивные или локальные параметры типа Xj существуют для каждой локальной точки системы (температура, плотность, давление) и имеют смысл термодинамических сил;
экстенсивные или интегральные параметры типа Yj принадлежат системе в целом (масса, объем, энтропия) и подчиняются свойству аддитивности равновесных значений параметров, а в трехмерном случае - градиентами интенсивных параметров;
Свойство аддитивности экстенсивных параметров позволяет адекватно представлять сложные, гетерогенные, многокомпонентные физические среды [12], как суперпозицию соответствующих подсистем, без усложнения применяемого аппарата. Указанные свойства, таким образом, являются основой термодинамических методов декомпозиции и агрегирования, позволяющих распространить свойства и характеристики элементов и подсистем на системы различного уровня сложности [10-16].
В классической термодинамике термодинамические величины и соотношения вводятся для равновесных состояний физических систем [12], при условии протекания квазистатических обратимых процессов, где такие величины, как температура, энтропия, существуют только для равновесных состояний. Реальные физические системы характеризуются принципиально неравновесными состояниями и соответственно необратимыми процессами, поэтому в соответствии с теорией о локальном равновесии имеем [7,8,10]:
 (28) (28)
или
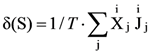 (29) (29)
Функция diS/dt, называемая производством энтропии, включает составляющие, относящиеся к необратимым процессам различного тензорного ранга:
- химические реакции,
- тепловые потоки,
- перенос вещества,
- электромагнитные процессы,
- вязкие явления.
Каждая из этих составляющих содержит два типа сомножителей [12]:
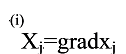 - обобщенные внутренние термодинамические силы, определяемые разностью неравновесных и равновесных значений параметров, а в трехмерном случае - градиентами интенсивных параметров; - обобщенные внутренние термодинамические силы, определяемые разностью неравновесных и равновесных значений параметров, а в трехмерном случае - градиентами интенсивных параметров;
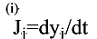 - потоки или скорости необратимых процессов сопряженные с соответствующими экстенсивными параметрами и определяемые изменением их во времени. - потоки или скорости необратимых процессов сопряженные с соответствующими экстенсивными параметрами и определяемые изменением их во времени.
Протекание необратимых процессов сопровождается производством энтропии в результате диссипации энергии:
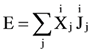 (30) (30)
Согласно 2-му закону термодинамики deltaS >0. При термодинамическом равновесии (вблизи состояния локального равновесия) зависимости между потоками и силами линейны:
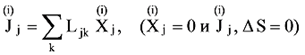 (31) (31)
где Ljk - линейные коэффициенты, подчиняющиеся соотношениям Онсагера.
В соответствии с теоремой Пригожина общее условие устойчивости записывается в виде обобщенных критериев эволюции термодинамических систем по производству энтропии [7,10]:

Используя теорему Пригожина и критерии устойчивости, интегральный критерий эволюции физических систем можно представить в виде [12]:
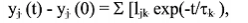 (32) (32)
где yj(0) - неравновесные или стационарные значения соответствующих параметров системы; tk - времена релаксации соответствующих необратимых процессов в системе; ljk - кинетические коэффициенты.
Очевидно, что в аналогичной форме суперпозиции экспоненциальных функций, можно представить интегральный процесс эволюции (релаксации) любых систем [7-12].
Следовательно, интегральные эволюционные и локальные процессы нарушения термодинамической устойчивости – взаимосвязаны, и в качестве такой связи между теорией термодинамического равновесия и теорией необратимых процессов является теория флуктуаций, вероятность возникновения которых для равновесных и локально-равновесных состояний определяется по формуле Эйнштейна [7,10]:
P = B exp (∆S/k) (33)
Если определить параметр - В, как «функцию масштаба начальной вероятности флуктуации», которую в данном случае можно получить интегрированием интенсивности отказа при хранении – λО, т.е. из уравнения (13), а в качестве Р использовать статистическую вероятность отказа, то логарифмирование уравнения (33) дает возможность «обратного перевода» вероятностных характеристик в функцию производства энтропии [10].
k∙(lnP - lnB) = ∆S (34)
Вероятностно-физический метод стендовых испытаний
При испытаниях РЭА и ЭП на надежность и безопасность всегда приходится решать задачу максимально эффективного использования возможностей их физических (стендовых) испытаний, в т.ч. для подтверждения конструкторских расчетов и качества выпускаемой продукции.
Технико-экономическими ограничениями при этом являются [12]:
- общая продолжительность испытаний (реально не более 2-3 месяцев при круглосуточной загрузке стенда);
- количество испытываемых изделий, с учетом разрушающего характера испытаний (реально - не более 3-5);
- затраты на идентификацию всех возникающих отказов элементов и на оперативное восстановление изделий в ходе испытаний (помимо сопровождения самого процесса испытаний).
В качестве основных физических ограничений выступают [12,13]:
- высокая надежность ЭРЭ, как причина слабой или практически нулевой наблюдаемости отказов ЭРЭ некоторых типов даже при продолжительных испытаниях;
- малая доля информативных отказов в общей массе наблюдаемых отказов, т.е. низкий процент однозначно идентифицируемых (параметрических) отказов (дефектность ЭРЭ, несоответствие нагрузочных характеристик и т.д.), в том числе «опасных» (коротких замыканий, пробоев и т.п.);
- ограниченные возможности корректного ускорения появления отказов в испытаниях с помощью повышения температуры среды и применения циклической электрической нагрузки, т.к. считается, что при ускорении деградации ЭРЭ более чем в 100 раз происходит существенное перераспределения отказов по причинам, интенсивностям, формам проявления и т.д.
Указанные ограничения предопределяют место экспериментальных методов в общей схеме проверки испытываемых изделий на соответствие требованиям квалиметрии, надежности и безопасности [13]. До настоящего времени они не позволяли продуктивно использовать экспериментальный этап для уточнения справочных интенсивностей отказов, но при надлежащей формулировке статистического критерия оставляли возможность экспериментально проверить расчетные оценки вероятностей.
Разработанный критерий сравнения проектных величин с результатами стендовых испытаний [10], основывается на разработанных физико-химических моделях и методах [12], что позволяет более точно оценивать все необходимые параметры. При этом решающим обстоятельством в выборе статистического критерия, связываемого с экспериментальными методами, является придание ему свойства относительной нечувствительности к неконтролируемому перераспределению пропорций в интенсивностях отказов ЭРЭ при форсировании испытаний изделий «ударными и циклическими» нагрузками [13,18].
Математическая модель стендовых испытаний
Пусть после завершения экспериментальных испытаний с восстановлениями отказывающих элементов всего получено N отказов ЭРЭ, в том числе o опасных отказов, m (m ≥ О) из которых вызвали опасные ситуации (пробой, воспламенение, дым и т.д.). За счет длительности форсированных испытаний количество опасных отказов o будетне слишком мало (иначе статистические выводы будут грубыми), а «ударный» режим «термобароциклирования» испытываемых изделий выбран так (в пределах ТУ), что вероятности опасных ситуаций высоки при наибольшей интенсивности отказов (например, выше 0,1).
Обозначим имевшие место опасные отказы через Пi(i =1,o) и будем рассматривать их как осуществленные взаимно независимые испытания, каждое из которых имело возможность завершиться одним из двух исходов - появлением или не появлением события C, означающего опасную ситуацию в изделии (испытания П независимы именно относительно события C).
Пусть, вычисленные любым способом, вероятности события C в каждом из испытаний Пi , а qi = 1 - рi - вероятности противоположного события C в этих испытаниях. Тогда данная совокупность независимых испытаний Пi с указанными вероятностями рi, qi (pi + qi = 1) представляет собой обобщенную схему независимых испытаний Бернулли с переменными вероятностями, приводящую к определенному распределению значений случайной величины ξ суммарного количества исходов C при реализации совокупности испытаний Пi (i=1,ō). Это распределение задается вероятностями Рк = Р (ξ=k), где Р(ξ= k) - вероятность того, что ξ принимает значение k.
Статистическим критерием расчетных вероятностей является проверка того, что каждая из вероятностей Р(ξ≤m) = Р(ξ≥m) оказывается не меньше Pi(i=1,ō)заранее заданного числа L/2 , где L - уровень значимости.
Указанные вероятности вычисляются по формулам [10,11,16]:
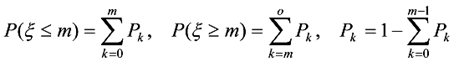 (35) (35)
а вероятности Рк(k = 0,ō) для случайной величины ξ , имеющей обобщенное биномиальное распределение с параметрами (o, р1 , р2 ,... рo ), (0 <р < 1, i = 1,ō), определяются выражениями:
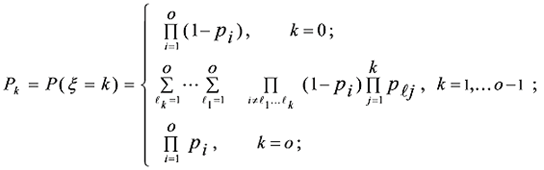 (36) (36)
При этом математическое ожидание М [ξ] и дисперсия D [ξ] случайной величины ξ, как это непосредственно следует из теорем о математическом ожидании и дисперсии, равны
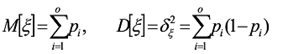 при при 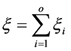 (37) (37)
где ξ - взаимно независимые случайные величины, принимающие значения 1 и 0 в испытаниях Пi, соответственно с вероятностями рi и qi, т.е. имеющие распределения Бернулли с параметрами р1, р2, ... ро соответственно.
В тех случаях, когда все рi - невелики, оказывается М[ξ] ≈ D[ξ]и подобно обычному биномиальному распределению можно, для упрощения расчетов, аппроксимировать указанное распределение (36) с достаточной точностью распределением Пуассона с параметром α = М [ξ], что подтверждается сравнением соответствующих характеристических функций:
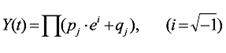 (38) (38)
Для практического применения является полезным следующее представление дисперсии D[ξ]:
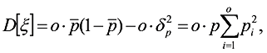 (39) (39)
где р и бр- соответственно выборочное среднее и дисперсия "варианты" рпо заданной совокупности значений р :
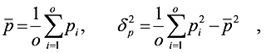 (40) (40)
Данное выражение указывает на то, что дисперсия рассматриваемого обобщенного биномиального распределения меньше дисперсии классического биномиального распределения с параметрами (о, p), причем меньше ровно на о дисперсий "варианты" p.
Таким образом, при планировании «интервалов электро-термо-баро-ударов» в стендовых испытаниях изделий [15] следует иметь в виду, что если средняя вероятность р будет оставаться постоянной, то максимум дисперсии D[ξ] будет соответствовать случаю р1 = р2 =.....= рn = р, а изменения рi в сторону их неодинаковости будут уменьшать флуктуации случайной величины ξ. Без (40) этот вывод мог бы показаться парадоксальным.
Методология реализации ускоренных испытаний
Системный анализ методов оценки надежности и ускоренных испытаний ЭРЭ, РЭА и ЭП [1,5-7], позволил выделить наиболее эффективные: американскую HAST-методику [21] и отечественные [9-20], а среди них - оптимальное направление исследований при создании стенда экспресс-диагностики изделий, в условиях тех ограничений, которые накладываются при ускорении процессов деградации полупроводников, диэлектриков и проводников [12,15].
В связи с тем, что безопасность изделий связана только с небольшой частью отказов, интенсивность которых, на один-два порядка ниже числа параметрических отказов, была обоснована взаимосвязь [9-12], необходимость [17] и эффективность [16,18] совмещения испытаний и оценки безопасности изделий и их надежности, с применением вероятностно–физических моделей. Таокй подход позволяет использовать все существующие методики и наработки в оценках, как параметров надежности (расходования ресурса), так и каждого опасного фактора: пожарной опасности, взрывоопасности, радиационной опасности, электpоопасности, токсичности, электромагнитной опасности, включая «человеческий фактор» [1,5,6,10-12], а также сконцентрировать дальнейшие усилия не на статистическом, а на их термодинамическом [7,8] или вероятностно-физическом комплексировании [12,19].
Ускоренными испытаниями РЭА и ЭП называются испытания указанных изделий в форсированных режимах с последующей экстраполяцией результатов к условиям испытаний при нормальных нагрузках [12,15].
Принимая во внимание, что результатом прогноза в нашем случае является момент времени выхода пожарных параметров за допустимые ГОСТ 12.1.004-91 границы (10-6), а натурные испытания проводятся на выборке (группе) из 3-х изделий, то предлагаемая методология является - групповой обратной методологией ускоренных испытаний [2,9-11].
Испытания 3-х электроприборов проводятся на стенде (рис.1), состоящем из следующего оборудования [10-12,13]:
1. Термобарокамеры с диапазонами изменения: температуры от минус 50˚ С до плюс 80˚ С и давления от 0,01 МПа до 0,2 МПа;
2. Пpогpаммно-технического комплекса "УНИКОНТ" УК-111 с комплектом измерительных модулей МККТП/ТC, АЦП-60 и коммутаторов повышенной мощности УФДC;
3. Комплекта интегрирующих термодатчиков (ИТДХК-68), измерительных термозондов (ИТЗТСМ-50) и измерительных шунтов (ИШRi);
4. Имитатора изменения переменного сетевого напряжения 187-242 в., мощностью до 0.9 - 8 квт. (ЛАТР и АТ-8 ОФ4.723.002П);
5. Рабочей станции (Intel Pentium);
6. Измерителей времени испытаний (таймеры УК 111 и РС).
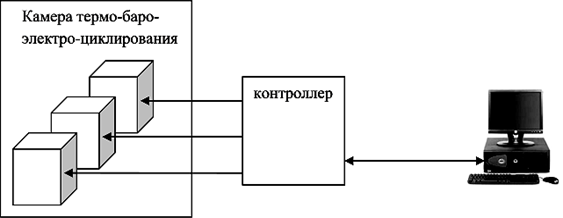
а) б) в)
Рисунок 1 - Стенд термо-баро-электро-циклирования: а) модернизированная камера 1 м3 (КТВ); б) контроллер «УНИКОНТ» (УК-111); в) рабочая станция
Все испытываемые изделия с установленными в них ИТД, ИТЗ и ИШ подключаются к испытательному стенду и помещаются в термобарокамеру, в которой с помощью РС и контроллера «УНИКОНТ» (рис. 2) устанавливаются средние по ТУ температура и давление для данного типа изделий, в которых они выдерживаются в течении 2-х часов.
После указанной выдержки изделие включают в рабочий режим с тестовой нагрузкой при сетевом напряжении 220 V 50 Гц [12], при котором их испытывают в течении суток (24 часа), после чего, полученные (установившиеся) температуры плат (блоков) и потребляемые ими мощности, обрабатываются программой расчета параметров надежности и пожарной опасности.

Рисунок 2 - Схема электрическая подключения контроллера «УНИКОНТ»
Далее, после «проветривания» термобарокамеры для остывания шунтов, датчиков и термозондов" до температуры средней по ТУ), описанный выше цикл измерений повторяется для сетевых напряжений 242 V и 187 V, 50 Гц, а затем изделия включают в режим с термо-баро-электро-циклированием, при сетевом напряжении 187 V 50 Гц. При этом термобароцикл должен иметь противофазные «квази-изотермические/квази-изобарические» участки (рис.3), во время которых должен «успевать» отрабатываться тест на работоспособность ЭП [12,13].
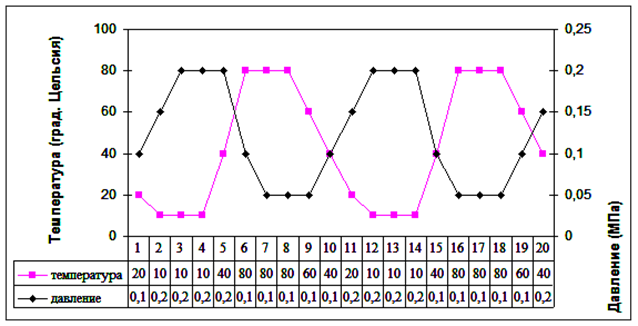
Рисунок 3 - Термо-баро-циклограмма (минуты)
Аналогично пониженному режиму (187 V) испытания проводятся для сетевых напряжений - 220 V и 242 V. Все полученные данные температурных и энергетических колебаний блоков РЭА или ЭП в целом обрабатываются программой расчета, а если в ходе испытаний происходит отказ ЭРЭ, плат и блоков электроприбора, то изделие подвергается восстановительному ремонту с фиксацией времени наработки и причины отказа. Пожароопасный отказ автоматически фиксируется УК 111 по изменению потребляемой мощности, измеряемой ИШ и соответствующему росту температуры зон, измеряемых ИТД и ИТЗ.
В таких режимах РЭА или ЭП испытывают до появления ОФП (опасных факторов пожара по ГОСТ 12.1.004), т.е. дыма или воспламенения какого-либо ЭРЭ или ЭРМ [12,13].
Если за рассчитанный срок испытаний с учетом электроциклирования воспламенение РЭА или ЭП не произошло, то изделие считается пожаробезопасным с точечными данными, полученными расчетным путем, но с более грубой доверительной оценкой при "нулевых наблюдениях" [12,13].
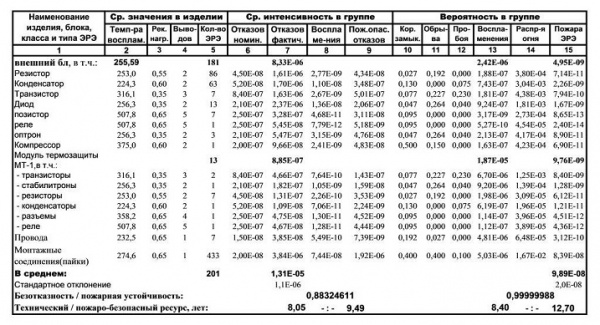
Проведенные исследования РЭА и ЭП с применением разработанных вероятностно-физических моделей свидетельствуют о том [10,15-17], что при использовании как отечественных, так и импортных ЭРЭ и рекомендуемых режимов их применения, имеет место низкий уровень их надежности и безопасности (табл.1).
Таблица 1. Надежность и пожарная безопасность ПЭВМ
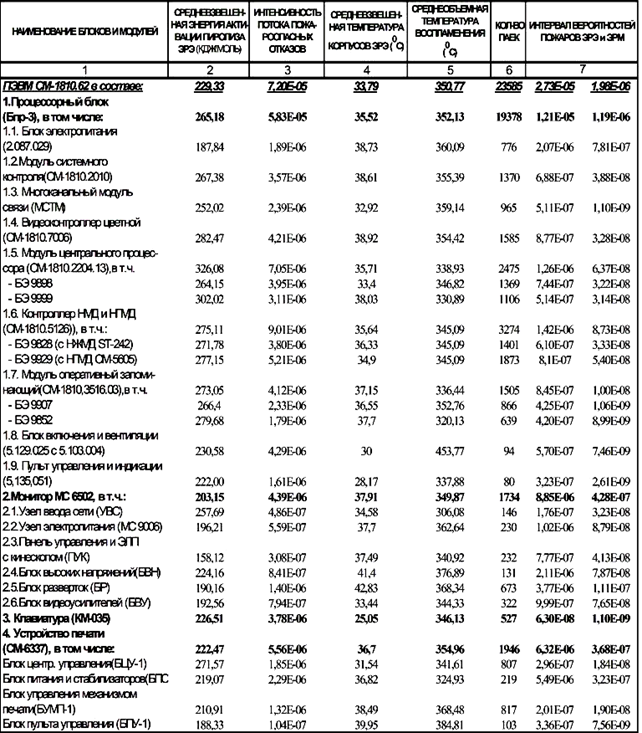
Так, например, пожарная опасность отечественного персонального компьютера (ПК) СМ-1810.62 в 27,3 раза превысила допустимый уровень вероятности пожара – 10-6, обусловленный государственным стандартом.
За исключением клавиатуры. все остальные блоки и устройства оказывались опасными уже через несколько десятков часов их эксплуатации, т.к. процессорный блок в 12,1 раза превысил допустимый уровень пожарной безопасности, монитор – в 8,8 раза, а устройство печати – в 6,3 (табл.1).
Таблица 2 - Надежность и пожарная безопасность лабораторных ЭП
Аналогичные результаты были получены при испытаниях средств вычислительной техники Украины и Литовской мини ЭВМ СМ-1700, а также при испытаниях лабораторных (таб.2) и бытовых (таб.3) электроприборов [10,13].
Таблица 3 - Надежность и пожарная безопасность бытовых ЭП
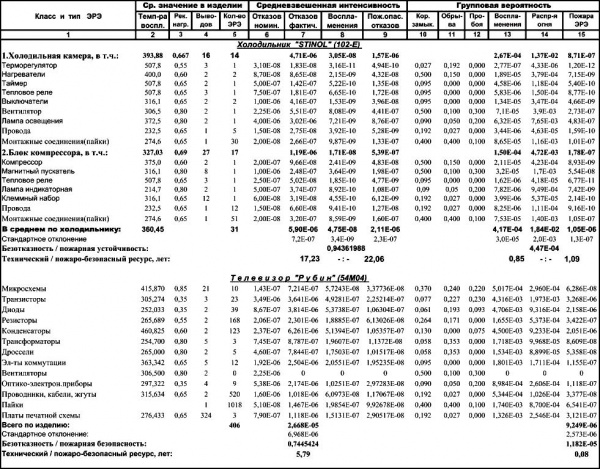
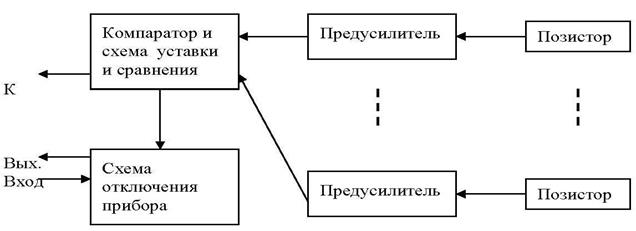
Рисунок 4 - Блок схема МСТЭЗ
Моделирование вариантов повышения надежности и снижения опасности РЭА и ЭП привели к созданию [15,16] модулей (рис.4) термоэлектронной защиты (МСТЭЗ), применение которых (при тех же конструктивных и схемотехнических решениях) поднимает уровень пожарной безопасности изделий более чем в 11 раз (таб.4), т.к. отключает их от электроэнергии при возникновении пожароопасного отказа, не допуская возникновения загорания, тем самым, делая практически соизмеримыми их эксплуатационный и пожаробезопасный ресурс [21].
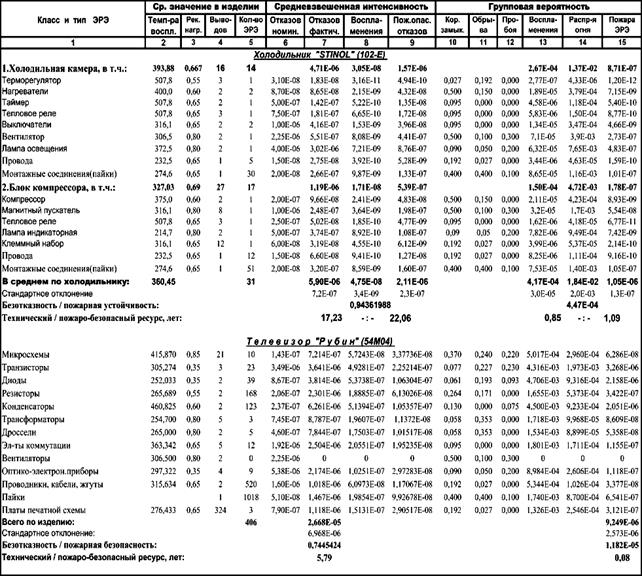
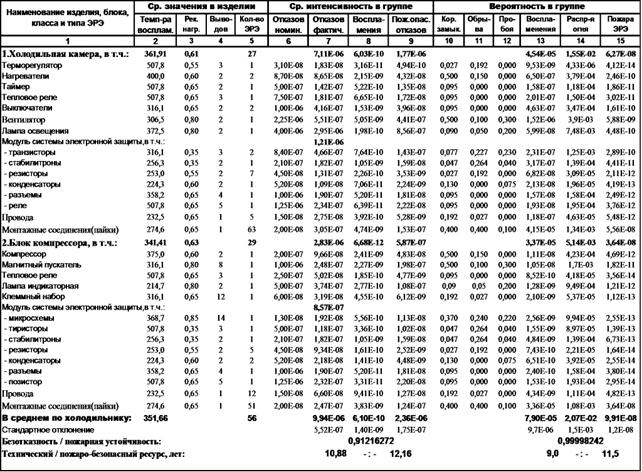
Таблица 4 - Надежность и безопасность холодильника с двумя МТЭЗ
Схемотехническая реализация МСТЭЗ (рис.4) зависит от сложности и конструктивных особенностей РЭА и ЭП т.е. определяется количеством термозондов, контролирующих тепловые потоки, и мощностью РЭА и ЭП, т.к. требует выбора тиристора или симистора, отключающих их от сети [24].
По аналогии с МТЭЗ, для современного отечественного телевизора «Горизонт» (таб.5) был разработан модуль КИП (с вентилятором и дымовым пожарным извещателем ИП 212-45).
Таблица 5 - Надежность и безопасность телевизора «Horizont» с КИП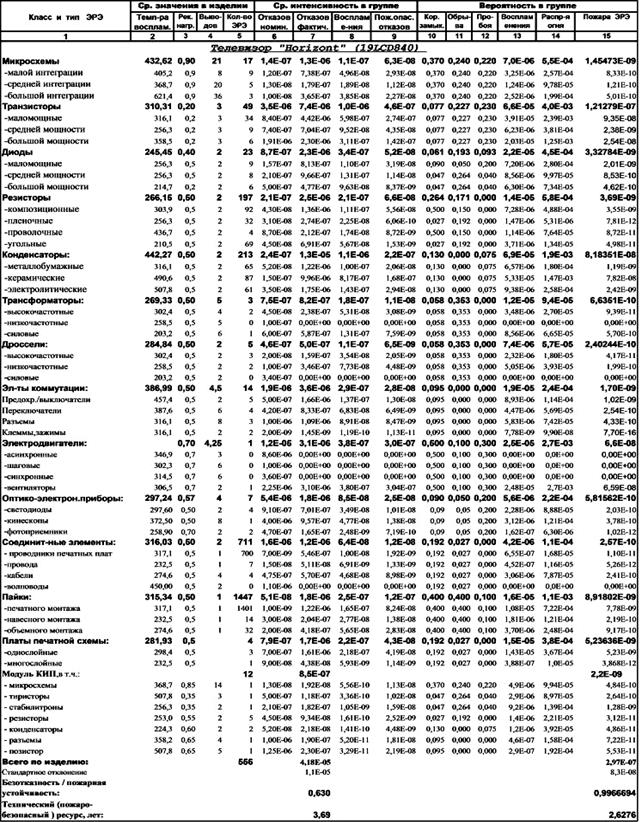
КИП, помимо воздушного охлаждения внутренних блоков, и «прокачивания» через ИП 212-45 воздуха помещения, в котором установлен телевизор, реализует тем самым, «псевдоаспирационный режим» [25] и подключается к соответствующим блокам, обеспечивая обнаружение ОФП, в т.ч. в режиме «сна». При этом пожаробезопасный ресурс был получен соизмеримым с техническим ресурсом (таб.5).
Модульные системы термоэлектронной защиты в автоматизации технологического прогона и приемо-сдаточных испытаний электроприборов.
При установке МСТЭЗ в ЭП, помимо решения проблемы их пожарной безопасности, т.е. автоматического отключения от электросети при появлении дополнительного пожароопасного тепловыделения, появляются следующие новые возможности, позволяющие повысить качество и надежность ЭП [13]:
- использование МСТЭЗ для организации ускоренного технологического прогона ЭП, вместо выборки группы изделий из промышленной серии и их испытаний, для «статистического распространения» параметров качества, надежности и безопасности на всю серию;
- если установить в МСТЭЗ разъем или порт (Wi-Fi или Bluetooth), на который вывести данные позисторов, то появляется возможность организовать для каждого ЭП или РЭА ускоренный технологический прогон с термоэлектроциклированием и тепловой локацией «их внутренностей» (без вскрытия изделий), что позволяет решить проблему прогнозирования наработки на отказ каждого изделия и его опасности, а также выявлению «ненадежных» ЭРЭ, «проскользнувших» в системе выходного контроля (у производителя ЭРЭ) и входного контроля (у производителя изделия), что является эффективным средством снижения отказов и потерь работоспособности до истечения спрогнозированного ресурса [10,15].
Как показали исследования [10-18], надежность самого изделия из-за дополнительных ЭРЭ, на которых реализована МСТЭЗ, может снижаться незначительно, т.к. в процессе его доработки и постановки на производство, появляется возможность «итерационного доведения» конструкции до оптимальной по «тепловому образу» каждого ЭРЭ и изделия в целом, получаемых по результатам ускоренного термоэлектропрогона.
Более того, использование данных МТЭЗ при ускоренном технологическом прогоне создает условия для формирования динамического гарантийного срока работы и ценообразования каждого ЭП или РЭА, вместо одинаковых гарантийных сроков и цен на всю серию [13]. Иными словами - вычисление наработки на отказ каждого изделия и его опасности по данным ускоренного технологический прогона с термо-электро-циклированием и внутренней тепловой локацией РЭА и ЭП с помощью МСТЭЗ, позволяет проставлять в паспорте каждого изделия вычисленный результат, как гарантийный срок работы, и изменять его цену, в соответствии надежностью и безопасностью каждого изделия [10].
А далее, если использовать данных ежегодной диагностики с МСТЭЗ (например, при гарантийном обслуживание РЭА и ЭП с МСТЭЗ), то возникает идея ежегодного контроля с помощью порта МСТЭЗ, при котором уточняется фактическая наработка, и возникает возможность изъять РЭА или ЭП в конце срока безопасной эксплуатации, предотвратив, таким образом, его отказ (аварию, пожар и т.д.) и возможные социально-экономические потери [13].
В частности [12,14], возможность получения и обработки данных о техническом и пожаробезопасном ресурсе каждого СВТ, создает принципиально новые условия повышения надежности различных АСУ, путем своевременной профилактике модулей и блоков, вероятность отказа в которых начинает превышать допустимый уровень. Это особенно важно в АСУТП объектов повышенной опасности (на АЭС, ГРЭС, НПЗ и т.д.).
Электроприборы - радиоизвещатели техносферной опасности и её навигации (РИТОН)
В среднем в России ежедневно в пожарах погибает около 60 человек и столько же травмируется, а прямой и косвенный материальный ущерб достигает 500,0 миллионов рублей в день. В том числе в жилом секторе в среднем ежедневно происходит 515 пожаров, в которых погибают 27 человек, и столько же травмируется. При этом наибольшая частота загораний происходит в интервале с 22 ч. вечера до 6 ч. утра, т.е. когда люди спят и не могут быстро среагировать [13,19].
Очевидно поэтому в некоторых странах (США, Германия, Польша) получили распространение автономные пожарные извещатели (АПИ), предназначенные для применения в жилых помещениях, выдающих, при обнаружении признаков пожара, прерывистый сигнал тревоги с уровнем звукового давления 85-90 дБ на расстоянии 1 м. от извещателя. Статистика свидетельствует, что применение АПИ позволяет сократить число погибших при пожарах в жилом секторе на 45% [13,15,19].
Если учесть, что более 60% пожаров возникает по электротехническим причинам (проводка, электронагревательные приборы, холодильники, телевизоры и т.д.), в которых погибают более 40% населения, то возникает идея совместить АПИ с ЭП, чем, во-первых, повысить его собственную безопасность, путем своевременного отключения от сети с помощью МСТЭЗ, если в нем возникает пожароопасный отказ, во-вторых, превратить его в устройство обнаруживающее загорание в жилом помещении вне электроприбора и оповещающее жильцов о необходимости эвакуации, в-третьих, расширить его функции оповещения об утечке бытового газа, а в-четвертых, предусмотреть наращивание функций на предмет охраны от несанкционированного проникновения в жилое помещение, включая реализацию оповещения с помощью радиоканала соответствующих «аварийных служб» (пожарной, газоаварийной и вневедомственной охраны и т.д.), как это было предложено при разработке такой системы [12,15].
Технология «интеллектуализации» была разработана в 2000 году для холодильника «СТИНОЛ-102», который являлся самым «пожароопасным» из всех холодильников, выпускаемых Липецким ЗАО «СТИНОЛ», т.к. содержал два электродвигателя-компрессора (рис.5,6), которые обеспечивали работу независимо и одновременно морозильной и холодильной камер [10,26].
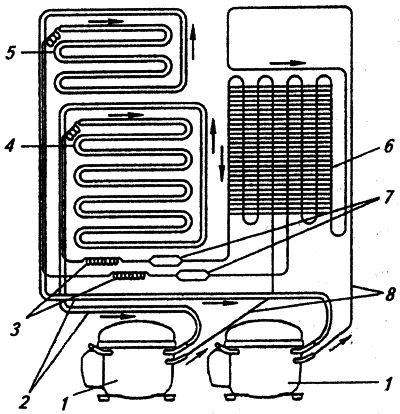
Рисунок 5 - Схема структурная агрегата
1 – компрессор, 2 - всасывающая трубка, 3 - капиллярная трубка,4 - испаритель ХК, 5 - испаритель МК, 6 – конденсатор, 7 - фильтр-осушитель, 8 - нагнетательная трубка
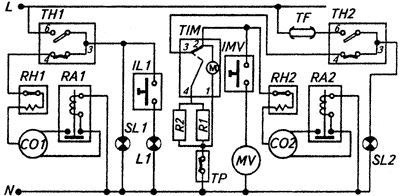
Рисунок 6 - Схема электрическая
L – Фаза, N – Нейтраль, ТН1 – терморегулятор холодильной камеры, ТН2 - терморегулятор морозильной камеры, RH1 - тепловое реле компрессора холодильной камеры, RA1 - пусковое реле компрессора холодильной камеры, RH2 - тепловое реле компрессора морозильной камеры, RA2 - пусковое реле компрессора морозильной камеры SL1 - индикаторная лампа холодильной камеры, SL2 - индикаторная лампа морозильной камеры, IL1 - выключатель лампы освещения холодильной камеры, L1 - лампа освещения холодильной камеры, TIM – таймер, TR - тепловое реле электронагревателя испарителя, IMV - выключатель вентилятора, MV – вентилятор, TF - тепловой плавкий предохранитель, CO1 - компрессор холодильной камеры, CO2 - компрессор морозильной камеры, R1 - электронагреватель испарителя, R2 - электронагреватель поддона испарителя
Модель «интеллектуализации СТИНОЛ-102» включала установку внутри корпуса холодильника проточного дымового пожарного извещателя с радиоканалом, при использовании дополнительной секции электровентилятора, который работает в системе автоматической оттайки (No Frost), и установкой МСТЭЗ в наиболее пожароопасных зонах (рис.7).
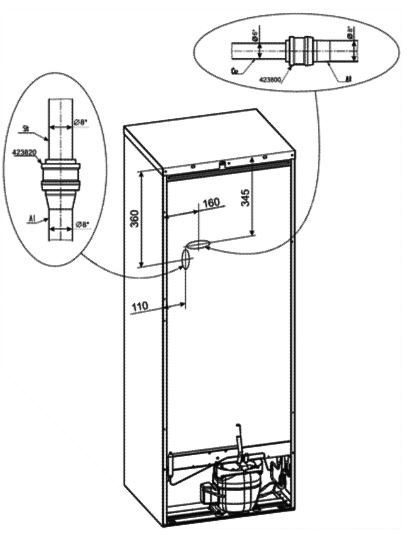
Рисунок 7 - Блок-схема холодильника-извещателя
В этом случае алгоритм круглосуточной «охраны кухни» можно представить в виде трех параллельных процессов [13,26]:
а) процесс нерерывного теплового контроля «пожароопасных зон» самого холодильника и отключение его от сети с помощью семисторов, если температура зоны превысит допустимую, с выдачей звукового аварийного сигнала «пожароопасный отказ»;
б) процесс «прокачки» объема воздуха в кухне через автономный пожарный извещатель с помощью электровентилятора и выдача прерывистого звукового сигнала «опасное задымление» в случае обнаружения «пороговой концентрации» дыма в помещении;
в) 3-х кратная верификация в течение 30 секунд концентрации дыма и, в случае непринятия жильцами мер блокировки сигнала «опасное задымление», отключение холодильника от сети с помощью семисторов и выдача непрерывного звукового сигнала «пожар», а также передача по радиоканалу сообщения на приемно-контрольный прибор в доме или прямо на ЦУСС сигнала «пожар».
В некоторых моделях холодильников «СТИНОЛ» (002,003,022,125 и 126) применяется электронная система управления вместо обычной электромеханической [13]. В таких холодильниках все функции контроля и управления сосредоточены в электронном блоке управления (рис.8).
При помощи термочувствительных датчиков, электронный блок управления собирает информацию о текущей температуре испарителей и воздуха внутри камер холодильника и управляет включением/отключением той или иной нагрузки (компрессоры, нагреватели, вентилятор и т.д.), включая самодиагностику и управление оттайкой «No Frost» [10,26].
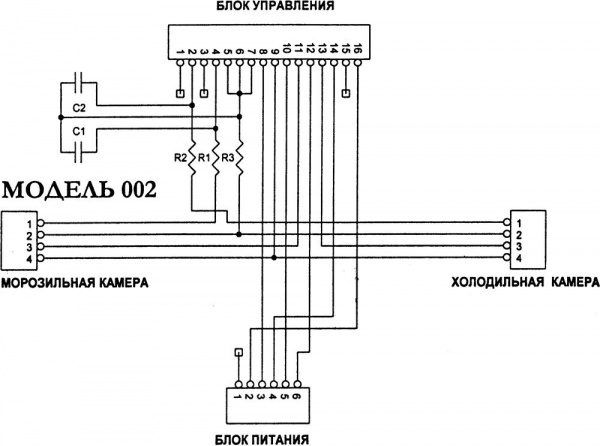
Рисунок 8 - Блок-схема электронного управления холодильником
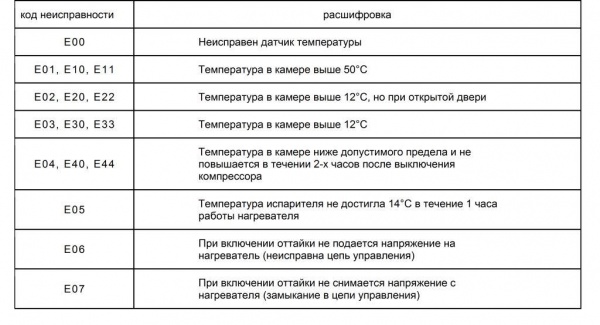
В случае обнаружения неисправности, на цифровом табло холодильника высвечивается соответствующий код (таб.6).
Таблица 6 - Система самодиагностики электронного блока
Возникновение аварийной ситуации сопровождается звуковым сигналом, свечением красного светодиода и кодом ошибки. Звуковой сигнал и код ошибки сбрасывается при нажатии любой кнопки, а с свечение красного светодиода сбрасывается только после устранения аварийной ситуации [13,26]. В этом случае функции МСТЭЗ и управление проточным извещателем, включая функцию отключения всех агрегатов при пожароопасном отказе, может быть возложена на электронный блок, при его соответствующей доработке [10,26].
По аналогии с холодильником могут быть «интеллектуализированы» телевизоры (таб.7), кондиционеры, сплит-системы (таб.8,9), СВЧ-печи и электросчетчики, защищая помещения, в которых они установлены [25-29].
Таблица 7- Надежность и безопасность телевизора «Рубин» с МСТЭЗ
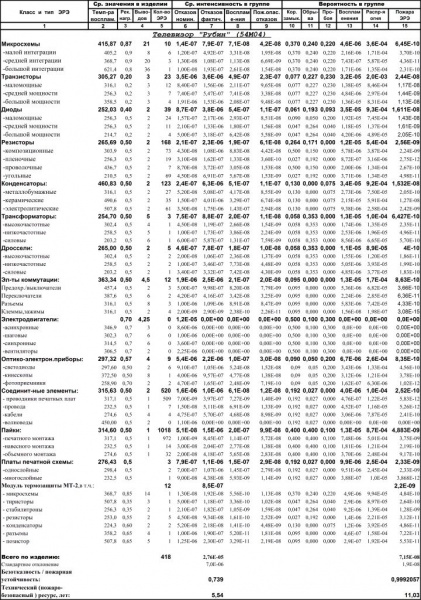
Таблица 8 - Надежность и безопасность внутреннего блока сплит-системы
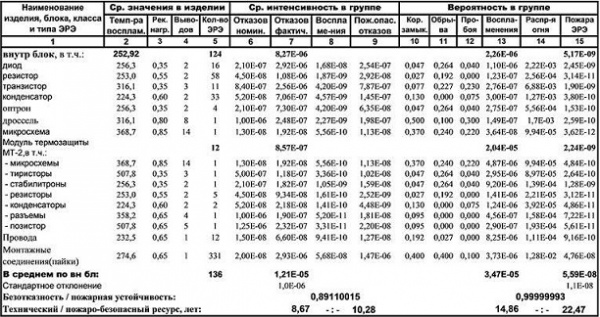
Таблица 9 - Надежность и безопасность внешнего блока сплит-системы
Следовательно, если «превратить» телевизоры и холодильники, электросчетчики и сплит-системы в автономные пожарные извещатели, то появляется возможность [10]:
- предотвратить 38,08% пожаров, которые произошли по электротехническим причинам;
- осуществить с их помощью раннее обнаружение, а следовательно и сокращение социально-экономических потерь 24,98% пожаров.
Дальнейшая «интеллектуализация» ЭП, как это отмечалось выше, возможна путем расширения функций МСТЭЗ металлооксидными (например, электрохимическими) датчиками на бытовой газ и ультразвуковыми доплеровскими датчиками обнаружения проникновения (перемещения) в помещения, при сооветствующей дифференциации сигналов вызова «аварийных служб» (пожарной, газоаварийной и вневедомственной охраны) по GSM-модему [10,29].
Таким образом, «интеллектуализация» превращает бытовые электроприборы, оснащенные микропроцессрами, в изделия двойного применения, которые помимо основных функций (холодильник, телевизор и т.д.) реализуют функции изделий «пожарно-сторожевого» назначения (пожаро-взрыво извещателей, датчиков охраны), т.е. «превращаются», таким образом, в радиоизвещатели техносферной безопасности и её навигации (РИТОН) с помощью пассивной локации источника радиоизлучения [13,15].
Тогда в соответствии с Федеральным Законом «О пожарной безопасности» (ФЗ-69, ст., ст. 26 и 29) указанные изделия освобождались бы от налога на добавленную стоимость и от налога на прибыль, что создавало бы благоприятные условия для скорейшего внедрения этой инновационной технологии и продукции. Однако, благодаря законотворчеству Российских чиновников и депутатов, новый Налоговый Кодекс «положил конец этим льготам», и продукция, которая могла бы предотвратить пожары и смерть от них – не появилась до сих пор [31].
Библиография
1. Буловский П.И., Зайденберг М.Г. Надежность приборов систем управления /Справ. пос./, Л: Машиностроение, 1975.-238с.
2. ГОСТ 12.1.004 Пожарная безопасность. Общие требования.-М.: Изд. стандартов, 1992.-77с.
3. ГОСТ 12.1.044 (МЭК 79-4; ИСО 1182 и др.) Система стандартов безопасности труда. Пожаровзрывоопасность веществ и материалов. Номенклатура показателей и методы их определения-М.: Изд. стандартов, 1990.-143с.
4. ГОСТ 27.410-87 Методы контроля показателей надежности и планы контроля испытаний на надежность-М.: Изд. стандартов.
5. Испытания радиоэлектронной аппаратуры на надежность /Груничев А.С. и др. - М: Сов.радио,1969.-288с.
6. Погребинский С.Б., Стрельников В.П. Проектирование и надежность многопроцессорных ЭВМ-М.: Радио и связь, 1988.-168с.
7. Воробьев В.Л. Термодинамические основы диагностики и надежности микроэлектронных устройств-М.: Наука, 1989.-160с.
8. Белозеров В.В., Топольский Н.Г. Термодинамический метод оценки объектов повышенной опасности и риска поражения ими ноосферы // «Информатизация систем безопасности»: материалы 2-й межд. конф. ИСБ-93.-М.: ВИПТШ МВД РФ (МАИ), 1993. с.45-51.
9. Белозеров В.В., Топольский Н.Г, Смелков Г.И. Вероятностно-физический метод определения пожарной опасности радиоэлектронной аппаратуры // «Научно-техническое обеспечение противопожарных и аварийно-спасательных работ»: материалы ХII Всероссийской науч.-практ.конф.-М.: ВНИИПО, 1993. с.23-27.
10. Белозеров В.В. Методы, модели и средства автоматизации управления техносферной безопасностью: диссертация на соискание ученой степени доктора технических наук /Академия государственной противопожарной службы. Москва, 2013.-382с
11. Белозеров В.В., Волошин В.А., Белозеров В.В. Концепция общей опасности техногенной сферы /отчет о НИР № 4.65 от 15.02.1996 (Министерство образования и науки РФ) – Ростов н/Д: РГУ, 1998.-33с.
12. Модели диагностики надежности и безопасности СВТ и АСУ объектов техносферы / В.В. Белозеров, А.Ю. Любавский, С.Н. Олейников. ‒ М.: Издательский дом Академии Естествознания, 2015. – 130 с. URL: http://os.x-pdf.ru/20fizika/396036-1-b-modeli-diagnostiki-nadezhnosti-bezopasnosti-svt-asu-obektov.php
13. Белозеров В.В. Экспериментальные методы оценки качества, надежности и безопасности электроприборов // Технологии техносферной безопасности.-2009.-№ 5.-9с. URL: http://agps-2006.narod.ru/ttb/2009-5/09-05-09.ttb.pdf
14. Любавский А.Ю. О диагностике ресурсов вычислительной техники //Технологии техносферной безопасности.-2015.-№ 3.-6с. URL: http://agps-2006.narod.ru/ttb/2015-3/45-03-15.ttb.pdf (дата обращения: 30.09.2018).
15. Белозеров В.В., Олейников С.Н. Радиоизвещатели техносферной опасности и её навигации с Интернет-системой их функционирования //Фундаментальные исследования.-2013.-№ 10-13. С. 2843-2853. http://www.fundamental-research.ru/ru/article/view?id=32921(дата обращения: 30.09.2018).
16. Белозеров В.В., Загускин С.Л., Прус Ю.В., Самойлов Л.К., Топольский Н.Г., Труфанов В.Н. Классификация объектов повышенной опасности и вероятностно-физические модели оценки их устойчивости и безопасности // Безопасность жизнедеятельности.-2001.-№ 8. С. 34-40.
17. Белозеров В.В., Гольцов Ю.И., Кулешова Н.И., Шпак Л.А. Способ получения полупроводникового керамического материала на основе титана бария, легированного ниобием - Патент РФ на изобретение № 2060566 от 20.05.96, заявка 5041179/28 от 07.05.1992, опубл. 20.05.1996.
18. Белозеров В.В., Гольцов Ю.И., Шпак Л.А., Юркевич В.Э. Позисторные датчики температуры для стенда термоэлектропрогона изделий электронно-вычислительной техники // Известия Российской академии наук. Серия физическая.-1993.-Т. 57. № 6. С. 155-159.
19. Богуславский Е.И., Белозеров В.В., Богуславский Н.Е. Прогнозирование, оценка и анализ пожарной безопасности /под ред. проф. Богуславского Е.И., рек. УМО Минобразования РФ для строительных ВУЗов – Ростов н/Д: РГСУ, 2004.-151с.
20. Белозеров В.В. Автоматизированная система испытаний электрорадиоматериалов с контролем их пожарной опасности: дис….канд. тех. наук-Академия государственной противопожарной службы.-Москва, 2008.-148с.
21. Патент США 4352239 МКИ HOIL 21/447, опубл. 05.101982 HAST-методика.
22. Иыуду К.А. Надежность, контроль и диагностика вычислительных машин и систем.-М.:Высш.шк.,1989.-216с.
23. Белозеров В.В., Иванников В.Л., Топольский Н.Г., Шпак Л.А. Новые средства оценки пожарной опасности и предотвращения пожаров в изделиях электронной техники и электроустановках: в сб. докл. "Семинара по проблемам пожарной безопасности АЭС"/Хмельницкая АЭС,г.Нетежин,28.09-02.10.92/.-М.: Интератомэнерго, 1992, с.18-27.
24. Белозеров В.В., Тетерин И.М., Топольский Н.Г. Модульные системы безопасности электроприборов //Технологии техносферной безопасности.-2005.-№ 4-3 с.
25. Филатьева Н.А. Модель телевизора-извещателя пожаровзрывобезопасности //«Студенческий научный форум-2016»: мат-лы VIII Межд. студ. электрон. науч. конф. URL http://www.scienceforum.ru/2016/pdf/26987.pdf (дата обращения: 30.09.2018).
26. Кулягин И.А. Модель холодильника-извещателя пожаровзрывоопасности // «Студенческий научный форум-2016»: материалы VIII Междунар. студ. электр. науч. конф. URL http://www.scienceforum.ru/2016/pdf/26381.pdf (дата обращения: 30.09.2018).
27. Новые технологии и материалы в производстве и строительстве: вопросы проектирования, разработки и внедрения /В.В. Белозеров, П.В. Борков, С.А. Кобелева, С.Н. Олейников, Р.Р. Насыров, Р.Р. Даминев - М.: Издательство Перо, 2012.-148с.
28. Кулягин И.А. Интеллектуализация безопасности электротехнических установок (на примере сплит-систем) // Электроника и электротехника. — 2018.-№ 1.-С.19-26. DOI: 10.7256/2453-8884.2018.1.25832. URL: http://e-notabene.ru/elektronika/article_25832.html.
29. Долаков Т.Б., Олейников С.Н. Модель автоматизированной микросистемы учета энергоресурсов и пожаровзрывозащиты жилого сектора // Электроника и электротехника. — 2018.-№ 2.-С.48-72. DOI: 10.7256/2453-8884.2018.2.26131. URL: http://e-notabene.ru/elektronika/article_26131.html.
30. Белозеров В.В., Олейников С.Н. О пространственно-временном статистическом анализе пожаров-Современные проблемы науки и образования – 2013. – № 4, c. 58-66; URL: http://science-education.ru/ru/article/view?id=9805 (дата обращения: 30.09.2018).
31. Белозеров В.В. Синергетика безопасной жизнедеятельности /монография – Ростов н/Д: Изд. центр ЮФУ, 2015. – 420с.
References
1. Bulovskii P.I., Zaidenberg M.G. Nadezhnost' priborov sistem upravleniya /Sprav. pos./, L: Mashinostroenie, 1975.-238s.
2. GOST 12.1.004 Pozharnaya bezopasnost'. Obshchie trebovaniya.-M.: Izd. standartov, 1992.-77s.
3. GOST 12.1.044 (MEK 79-4; ISO 1182 i dr.) Sistema standartov bezopasnosti truda. Pozharovzryvoopasnost' veshchestv i materialov. Nomenklatura pokazatelei i metody ikh opredeleniya-M.: Izd. standartov, 1990.-143s.
4. GOST 27.410-87 Metody kontrolya pokazatelei nadezhnosti i plany kontrolya ispytanii na nadezhnost'-M.: Izd. standartov.
5. Ispytaniya radioelektronnoi apparatury na nadezhnost' /Grunichev A.S. i dr. - M: Sov.radio,1969.-288s.
6. Pogrebinskii S.B., Strel'nikov V.P. Proektirovanie i nadezhnost' mnogoprotsessornykh EVM-M.: Radio i svyaz', 1988.-168s.
7. Vorob'ev V.L. Termodinamicheskie osnovy diagnostiki i nadezhnosti mikroelektronnykh ustroistv-M.: Nauka, 1989.-160s.
8. Belozerov V.V., Topol'skii N.G. Termodinamicheskii metod otsenki ob''ektov povyshennoi opasnosti i riska porazheniya imi noosfery // «Informatizatsiya sistem bezopasnosti»: materialy 2-i mezhd. konf. ISB-93.-M.: VIPTSh MVD RF (MAI), 1993. s.45-51.
9. Belozerov V.V., Topol'skii N.G, Smelkov G.I. Veroyatnostno-fizicheskii metod opredeleniya pozharnoi opasnosti radioelektronnoi apparatury // «Nauchno-tekhnicheskoe obespechenie protivopozharnykh i avariino-spasatel'nykh rabot»: materialy KhII Vserossiiskoi nauch.-prakt.konf.-M.: VNIIPO, 1993. s.23-27.
10. Belozerov V.V. Metody, modeli i sredstva avtomatizatsii upravleniya tekhnosfernoi bezopasnost'yu: dissertatsiya na soiskanie uchenoi stepeni doktora tekhnicheskikh nauk /Akademiya gosudarstvennoi protivopozharnoi sluzhby. Moskva, 2013.-382s
11. Belozerov V.V., Voloshin V.A., Belozerov V.V. Kontseptsiya obshchei opasnosti tekhnogennoi sfery /otchet o NIR № 4.65 ot 15.02.1996 (Ministerstvo obrazovaniya i nauki RF) – Rostov n/D: RGU, 1998.-33s.
12. Modeli diagnostiki nadezhnosti i bezopasnosti SVT i ASU ob''ektov tekhnosfery / V.V. Belozerov, A.Yu. Lyubavskii, S.N. Oleinikov. ‒ M.: Izdatel'skii dom Akademii Estestvoznaniya, 2015. – 130 s. URL: http://os.x-pdf.ru/20fizika/396036-1-b-modeli-diagnostiki-nadezhnosti-bezopasnosti-svt-asu-obektov.php
13. Belozerov V.V. Eksperimental'nye metody otsenki kachestva, nadezhnosti i bezopasnosti elektropriborov // Tekhnologii tekhnosfernoi bezopasnosti.-2009.-№ 5.-9s. URL: http://agps-2006.narod.ru/ttb/2009-5/09-05-09.ttb.pdf
14. Lyubavskii A.Yu. O diagnostike resursov vychislitel'noi tekhniki //Tekhnologii tekhnosfernoi bezopasnosti.-2015.-№ 3.-6s. URL: http://agps-2006.narod.ru/ttb/2015-3/45-03-15.ttb.pdf (data obrashcheniya: 30.09.2018).
15. Belozerov V.V., Oleinikov S.N. Radioizveshchateli tekhnosfernoi opasnosti i ee navigatsii s Internet-sistemoi ikh funktsionirovaniya //Fundamental'nye issledovaniya.-2013.-№ 10-13. S. 2843-2853. http://www.fundamental-research.ru/ru/article/view?id=32921(data obrashcheniya: 30.09.2018).
16. Belozerov V.V., Zaguskin S.L., Prus Yu.V., Samoilov L.K., Topol'skii N.G., Trufanov V.N. Klassifikatsiya ob''ektov povyshennoi opasnosti i veroyatnostno-fizicheskie modeli otsenki ikh ustoichivosti i bezopasnosti // Bezopasnost' zhiznedeyatel'nosti.-2001.-№ 8. S. 34-40.
17. Belozerov V.V., Gol'tsov Yu.I., Kuleshova N.I., Shpak L.A. Sposob polucheniya poluprovodnikovogo keramicheskogo materiala na osnove titana bariya, legirovannogo niobiem - Patent RF na izobretenie № 2060566 ot 20.05.96, zayavka 5041179/28 ot 07.05.1992, opubl. 20.05.1996.
18. Belozerov V.V., Gol'tsov Yu.I., Shpak L.A., Yurkevich V.E. Pozistornye datchiki temperatury dlya stenda termoelektroprogona izdelii elektronno-vychislitel'noi tekhniki // Izvestiya Rossiiskoi akademii nauk. Seriya fizicheskaya.-1993.-T. 57. № 6. S. 155-159.
19. Boguslavskii E.I., Belozerov V.V., Boguslavskii N.E. Prognozirovanie, otsenka i analiz pozharnoi bezopasnosti /pod red. prof. Boguslavskogo E.I., rek. UMO Minobrazovaniya RF dlya stroitel'nykh VUZov – Rostov n/D: RGSU, 2004.-151s.
20. Belozerov V.V. Avtomatizirovannaya sistema ispytanii elektroradiomaterialov s kontrolem ikh pozharnoi opasnosti: dis….kand. tekh. nauk-Akademiya gosudarstvennoi protivopozharnoi sluzhby.-Moskva, 2008.-148s.
21. Patent SShA 4352239 MKI HOIL 21/447, opubl. 05.101982 HAST-metodika.
22. Iyudu K.A. Nadezhnost', kontrol' i diagnostika vychislitel'nykh mashin i sistem.-M.:Vyssh.shk.,1989.-216s.
23. Belozerov V.V., Ivannikov V.L., Topol'skii N.G., Shpak L.A. Novye sredstva otsenki pozharnoi opasnosti i predotvrashcheniya pozharov v izdeliyakh elektronnoi tekhniki i elektroustanovkakh: v sb. dokl. "Seminara po problemam pozharnoi bezopasnosti AES"/Khmel'nitskaya AES,g.Netezhin,28.09-02.10.92/.-M.: Interatomenergo, 1992, s.18-27.
24. Belozerov V.V., Teterin I.M., Topol'skii N.G. Modul'nye sistemy bezopasnosti elektropriborov //Tekhnologii tekhnosfernoi bezopasnosti.-2005.-№ 4-3 s.
25. Filat'eva N.A. Model' televizora-izveshchatelya pozharovzryvobezopasnosti //«Studencheskii nauchnyi forum-2016»: mat-ly VIII Mezhd. stud. elektron. nauch. konf. URL http://www.scienceforum.ru/2016/pdf/26987.pdf (data obrashcheniya: 30.09.2018).
26. Kulyagin I.A. Model' kholodil'nika-izveshchatelya pozharovzryvoopasnosti // «Studencheskii nauchnyi forum-2016»: materialy VIII Mezhdunar. stud. elektr. nauch. konf. URL http://www.scienceforum.ru/2016/pdf/26381.pdf (data obrashcheniya: 30.09.2018).
27. Novye tekhnologii i materialy v proizvodstve i stroitel'stve: voprosy proektirovaniya, razrabotki i vnedreniya /V.V. Belozerov, P.V. Borkov, S.A. Kobeleva, S.N. Oleinikov, R.R. Nasyrov, R.R. Daminev - M.: Izdatel'stvo Pero, 2012.-148s.
28. Kulyagin I.A. Intellektualizatsiya bezopasnosti elektrotekhnicheskikh ustanovok (na primere split-sistem) // Elektronika i elektrotekhnika. — 2018.-№ 1.-S.19-26. DOI: 10.7256/2453-8884.2018.1.25832. URL: http://e-notabene.ru/elektronika/article_25832.html.
29. Dolakov T.B., Oleinikov S.N. Model' avtomatizirovannoi mikrosistemy ucheta energoresursov i pozharovzryvozashchity zhilogo sektora // Elektronika i elektrotekhnika. — 2018.-№ 2.-S.48-72. DOI: 10.7256/2453-8884.2018.2.26131. URL: http://e-notabene.ru/elektronika/article_26131.html.
30. Belozerov V.V., Oleinikov S.N. O prostranstvenno-vremennom statisticheskom analize pozharov-Sovremennye problemy nauki i obrazovaniya – 2013. – № 4, c. 58-66; URL: http://science-education.ru/ru/article/view?id=9805 (data obrashcheniya: 30.09.2018).
31. Belozerov V.V. Sinergetika bezopasnoi zhiznedeyatel'nosti /monografiya – Rostov n/D: Izd. tsentr YuFU, 2015. – 420s.
Ссылка на эту статью
Просто выделите и скопируйте ссылку на эту статью в буфер обмена. Вы можете также
попробовать найти похожие
статьи
|
|



