|
ГЛАВНАЯ
> Вернуться к содержанию
Кибернетика и программирование
Правильная ссылка на статью:
Галанина Н.А., Иванова Н.Н., Песошин В.А.
Способы реализации устройств кодирования цифровых сигналов вычетами в системе остаточных классов
// Кибернетика и программирование.
2013. № 1.
С. 21-36.
DOI: 10.7256/2306-4196.2013.1.8311 URL: https://nbpublish.com/library_read_article.php?id=8311
Способы реализации устройств кодирования цифровых сигналов вычетами в системе остаточных классов
Галанина Наталия Андреевна
доктор технических наук
профессор, кафедра математического и аппаратного обеспечения информационных систем, Чувашский государственный университет имени И.Н. Ульянова
428015, Россия, г. Чебоксары, Московский пр-т, д. 15
Galanina Nataliya Andreevna
Doctor of Technical Science
Professor, Department of Mathematics and Hardware of Information Systems, Ulyanov Chuvash State University
428015, Russia, g. Cheboksary, Moskovskii pr-t, d. 15

|
galaninacheb@mail.ru
|
|
 |
Другие публикации этого автора
|
|
Иванова Надежда Николаевна
428015, г. Чебоксары, Московский пр-т, д. 15
Ivanova Nadezhda Nikolaevna
428015, g. Cheboksary, Moskovskii pr-t, d. 15

|
galaninacheb@mail.ru
|
|
 |
|
Песошин Валерий Андреевич
доктор технических наук
профессор, кафедра компьютерных систем, Казанский национальный исследовательский технический университет имени А.Н. Туполева
420111, Казань, ул. К.Маркса, д.10,
Pesoshin Valerii Andreevich
Doctor of Technical Science
420111, Kazan', ul. K.Marksa, d.10,

|
galaninacheb@mail.ru
|
|
 |
|
DOI: 10.7256/2306-4196.2013.1.8311
Дата направления статьи в редакцию:
18-01-2013
Дата публикации:
1-2-2013
Аннотация:
Проведен аналитический обзор способов реализации устройств кодирования входных сигналов вычетами в системе остаточных классов и обоснован выбор их оптимальных структур. Оценены аппаратурные и временные затраты рассмотренных схемотехнических решений. Цель исследования состоит в рассмотрении всех возможных вариантов кодирования входных сигналов в остаточных классах с учетом современной элементной базы и наиболее полным использованием преимуществ системы остаточных классов, оценке аппаратной и временной сложности этих вариантов и выборе и обосновании наилучшего решения с точки зрения выше обозначенных критериев. Аппаратурные затраты для логических шифраторов выражаются количеством двухвходовых логических элементов, а для ППЗУ приводятся в виде ее информационной емкости в битах. Аппаратурные затраты шифраторов на логических схемах зависят от того, на сколько частей делятся числа входной последовательности. Делается вывод, что возможно дальнейшее упрощение таких логических шифраторов и, как следствие, – сокращение аппаратурных затрат.
Ключевые слова:
кодирование, цифровой сигнал, остаточные классы, исследование, шифратор, интегральная схема, элементная база, биты, микросхемотехника, аппаратурные затраты
Abstract: The article presents an analytical review of ways to implement encoders input residues in the residue number system and justified their selection of optimal structures. Authors evaluates instrumental and time costs considered circuit solutions. The purpose of the study is to consider all possible options encoding input signals in residual classes with the modern element base and full advantage of the system of residual classes, evaluation of hardware and time complexity of these options and the selection and justification of the best solution in terms of the criteria indicated above. Hardware cost of encoders are expressed as logical number of two-input logical elements, and to an EPROM contained in the form of its information bits in capacity. Instrumental cost of encoders on logic circuits depends on how many parts the input sequence is divided. It is concluded that it is possible to further simplify logical encoders and, as a consequence, reduce hardware expenses.
Keywords: coding, digital signal, residual classes, research, scrambler, integrated circuit, the element base, bits, microcircuitry, hardware expenses
Введение Существенную часть общих аппаратурных затрат цифровых устройств фильтрации и спектрального анализа в системе остаточных классов (СОК) составляют шифраторы. Они преобразуют целые R-разрядные числа x(kT) в RS-разрядные вычеты xS(kT) по предварительно выбранным взаимно простым модулям NS (S=`bar(1,nu)`). При этом критерием выбора способа реализации устройств кодированияявляется минимум функции Fш = Dшtш, где Dш – число двухвходовых логических элементов в шифраторе, tш – время кодирования [2, 3]. При реализации проекта на логических блоках в виде последовательно включенных матриц элементов И и ИЛИ, либо их эквивалента в другом базисе исторически первым было стремление минимизировать число логических элементов в схеме [5]. С переходом на интегральные схемы (ИС) и ростом уровня их интеграции критерием аппаратурной сложности цифровых устройств (ЦУ) стала площадь, требуемая для их размещения. Для ИС, реализуемых на кристалле, площадь измеряется в квадратных миллиметрах, а для устройств на печатной плате – числом корпусов в составе цифрового устройства. Так как корпуса ИС отличаются размерами, то их следует приводить к некоторым эквивалентным корпусам. Операции приведения соответствует оценка суммарной площади корпусов ЦУ по общему числу всех выводов корпусов ИС. Отсюда следует, что, во-первых, характеристикой сложности ИС является уровень интеграции, оцениваемый либо числом базовых логических элементов, либо числом транзисторов, которые размещены на кристалле; а, во-вторых, между всеми перечисленными выше критериями сохраняется известная связь.
Цель исследования состоит в рассмотрении всех возможных вариантов кодирования входных сигналов в остаточных классах с учетом современной элементной базы и наиболее полным использованием преимуществ СОК, оценке аппаратной и временной сложности этих вариантов и выборе и обосновании наилучшего решения с точки зрения выше обозначенных критериев.
В связи с изложенным, в приведенных результатах исследований аппаратурные затраты для логических шифраторов выражаются количеством двухвходовых логических элементов, а для ППЗУ приводятся в виде ее информационной емкости в битах. «Битам» можно поставить в соответствие количество триггеров, а затем и транзисторов, пользуясь известными соотношениями, используемыми в микросхемотехнике:
1 ячейка памяти = 1 бит = 1 разряд = 1 триггер; 1 логический элемент = 4 – 6 транзисторов [4].
Возможно несколько способов кодирования в СОК. Первый – моделирование алгоритма [1] :
`x_s(kT)=x(kT)-~|(x(kT))/N_s|~ N_slt=x(kT)>modN_s`
где `~|x|~` означает целую часть числа x, т.е. наибольшее целое число, не превосходящее x. Второй способ предусматривает совмещение функций АЦП и шифратора и применяется в автономных спецпроцессорах. Мы остановимся на третьем методе: он используется при работе устройств в СОК со стандартными магистралями традиционных устройств в позиционной системе счисления (ПСС). В таких системах шифраторы ШS переводят позиционный код в СОК. При этом ШS могут быть реализованы на ППЗУ и на логических схемах (для указания этого различия при реализации устройств кодирования будет в дальнейшем использоваться термин «логический шифратор»).
Оценка аппаратурных и временных затрат при построении шифраторов на ППЗУ При реализации шифраторов СОК на ППЗУ задача решается следующим образом: исходный код числа x(kT) является адресом заранее вычисленного и запрограммированного вычета xS(kT); время кодирования составляет tш1 = tППЗУ. При реализации шифраторов на ППЗУ в качестве аппаратурных затрат можно рассматривать информационную емкость ППЗУ в битах. Так как разрядность чисел на входе ППЗУ равна R, а на выходе разрядность вычетов чисел в S-м канале СОК – RS, то аппаратурные затраты для одного канала СОК вычисляются по формуле Dш1 = RS2R (бит) [5]. В табл. 1 представлены значения Dш1 для одного канала СОК.
Таблица 1
Аппаратурные затраты (Dш1) для одного канала СОК, бит
|
Разрядность
вычета, бит
|
Разрядность входного числа, бит
|
Максимальное
и минимальное основания СОК
|
|
R = 8
|
R = 10
|
R = 12
|
R = 16
|
|
RS = 4
|
1024
|
4096
|
16 384
|
262 144
|
NSmax=13, NSmin=11
|
|
RS = 5
|
1280
|
5120
|
20 480
|
327 680
|
NSmax=31, NSmin=17
|
|
RS = 6
|
1536
|
6144
|
24 576
|
393 216
|
NSmax=61, NSmin=37
|
Сократить аппаратурные затраты можно с помощью разбиения входного числа x(kT) на n частей. Очевидно, что:
`x_(s)(kT)<=sum_(i=1)^nx_s_i>modN_s, (2)`
где `x_S_i<=x_i2^((sum_(j=1)^(i-1)r_j))>modN_s ;`
ri – разрядность i-й части числа x(kT), i =1, 2, …, n; r0 = 0.
ППЗУ i-й части вычета xS (xSi) перепрограммируется в соответствии с (2). Его схема будет выглядеть следующим образом:

Рис. 2. Схема шифратора при разбиении x(kT) на две части
Аппаратурные затраты Dш2 будут включать затраты на организацию памяти (DППЗУ = 2(R/2+1)RS бит), к которым добавятся затраты на логические схемы И (DИ = 2RS + 1) и модульные сумматоры (`D_sum=14R_s+1`).
Кроме того, если `R/2<R_S` , то затраты на организацию памяти уменьшаются вдвое (DППЗУ = 2R/2RS), так как в этом случае «младшее» ППЗУ будет отсутствовать, а все «младшие» разряды xмл = xS1.
Временные затраты составят:
tш2=tппзу+2tср(Rs+4); tср=(tзд0,1+tзд1,0)/2, где
где tср – время срабатывания логической схемы (ЛС); tзд0,1 и tзд1,0 -
время задержки включения и выключения ИС.
Для случая разбиения x(kT) общие затраты Dш2 приведены в табл. 2.
Таблица 2
Аппаратурные затраты (Dш2) для схемы на рис. 2, бит
|
Разрядность
вычета, бит
|
Разрядность входного числа, бит
|
|
R = 8
|
R = 10
|
R = 12
|
R = 16
|
|
RS = 4
|
194
|
322
|
578
|
2114
|
|
RS = 5
|
162*
|
402
|
722
|
2642
|
|
RS = 6
|
194*
|
290*
|
866
|
3170
|
Примечание. * – этот случай связан с отсутствием «младшего» ППЗУ.
Следовательно, при использовании схемы (рис. 2) удается существенно сократить аппаратурные затраты на реализацию шифраторов: для R = 8, 10, 12, 16 – соответственно в 7,1; 15,5; 28,4; 124 (раза).
Упрощенные варианты построения шифраторов на логических схемах Проведенные исследования показали, что для значения вычета RS ≤ 6 минимальное значение целевой функции Fш = min гарантируют логические шифраторы, в которых преобразование R-разрядного входного числа x(kT) в его RS-разрядный вычет происходит при использовании логических методов синтеза схем на основе матриц дизъюнкций и конъюнкций.
Исследования выявили периодичность вариантов и возможность логического вычисления остатков. Но такое решение допустимо для небольших значений модулей NS = 5 (или NS = 7) при RS = 3, а как показывает практика, число разрядов R входной последовательности x(kT) бывает достаточно большим. В этом случае предлагается разбиение R на несколько частей с дополнительным введением сумматора (по аналогии со случаем с ППЗУ (рис. 2)). На рис. 3 представлена схема шифратора с логическими схемами LS (LS1 соответственно для «младших» разрядов, а LS2 – для «старших»).
Сумматор SM выполняется на логических двухвходовых элементах, число которых равняется 14RS + 1. При его реализации обязательно учитываются знаки чисел, так как в СОК ` N=prod_(S=1)^nuN_s , `
а за "0" считается число N/2. Поэтому положительными будут числа `(N/2+R_i)N_s,`
а отрицательными, соответственно, числа `(N/2-R_i)N_s` .
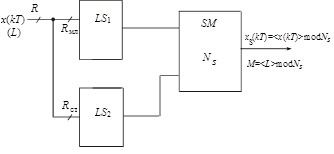
Рис. 3. Схема логического шифратора
при разбиении входной последовательности на две части
Аппаратурные затраты Fш шифраторов на логических схемах зависят от того, на сколько частей n по Ri разрядов делятся числа входной последовательности x(kT). Например, 10-разрядное число L на входе логического шифратора (рис. 3) можно разбить на 3 числа:
L=lст+lср+lмл ,
где lст = 3 (разряда); lср= 3 (разряда); lмл = 4 (разряда).
При этом Rст+Rср+Rмл = R = Rобщ; Rмл= Rs [3].
Проведенные исследования показали, что, во-первых, оптимальным является разбиение двоичного кода числа x(kT) на две части (n = 2); во-вторых, разбиение входной последовательности x(kT) на части нецелесообразно при разрядности чисел R < 8; в-третьих, R-разрядные входные числа делятся на старшую и младшую части (Rст и Rмл), каждая из которых имеет разрядность, равную R/2.
Количество двухвходовых конъюнкторов, входящих в состав логических схем LS1 (LS2), определяется по формуле: Dи=R+2R/2+13-`~|` 2R/2/Ns`|~`,
а количество дизъюнкторов Dили устанавливается по таблицам истинности.
Для практически интересного случая R = 10 аппаратурные затраты представлены в табл. 3
Таблица 3
Аппаратурные затраты шифраторов на логических схемах
|
NS
|
5
|
7
|
11
|
13
|
17
|
19
|
23
|
29
|
31
|
37
|
…
|
61
|
|
Dи
|
49
|
51
|
53
|
53
|
54
|
54
|
54
|
54
|
54
|
54
|
…
|
54
|
|
Dили
|
28
|
37
|
45
|
47
|
48
|
54
|
56
|
68
|
72
|
80
|
…
|
80
|
| |
77
|
88
|
98
|
100
|
102
|
108
|
110
|
122
|
126
|
129
|
…
|
129
|
Модулярные сумматоры содержат 14RS + 1 двухвходовых логических элементов. Максимальное время сложения в них tс = 2tср(RS + 2), т.е. в два раза больше, чем у обычного накапливающего сумматора. Окончательно получим следующие формулы для подсчета аппаратурных и временных затрат: Dш3 = 2DLS + DC; t1 = 3tср + tc = tср(7 + 2RS).
Значения Dш3 и t1 для такого случая шифраторов приведены в табл. 4.
Таблица 4
Аппаратурные (Dш3) и временные (t1) затраты шифраторов
|
NS
|
5
|
7
|
11
|
13
|
17
|
19
|
23
|
29
|
37
|
…
|
61
|
|
Dш3
|
211
|
233
|
272
|
276
|
299
|
311
|
315
|
339
|
372
|
…
|
372
|
|
t1/tср
|
13
|
13
|
15
|
15
|
17
|
17
|
17
|
17
|
19
|
…
|
19
|
Следует отметить, что возможно дальнейшее упрощение таких логических шифраторов и, как следствие, – сокращение аппаратурных затрат.
` `
Библиография
1. Акушский, И. Я. Машинная арифметика в остаточных классах / И.Я. Акушский, Д.И. Юдицкий. – М.: Сов. радио, 1968. – 440 с.
2. Галанина, Н. А. Реализация блоков шифрации и дешифрации сигналов в непозиционных устройствах ЦОС / Н.А. Галанина, Н.Н. Иванова, А.А. Иванов // Вестник Чувашского университета. – 2007. – № 2. – С. 166-173.
3. Лебедев, Е. К. Способы кодирования в непозиционных вычислительных устройствах / Е.К. Лебедев // Проектирование ЭВМ: межвуз. сб. науч. трудов. – Рязань: Изд-во РРТИ, 1992. – С. 104-109.
4. Стрекалов, Ю. А. Реализация арифметико-логического устройства, функционирующего в системе счисления в остаточных классах на ПЛИС / Ю.А. Стрекалов // Инфокоммуникационные технологии. – 2004. – Т. 2. – № 4. – С. 46-48.
5. Угрюмов, Е. П. Цифровая схемотехника: учеб. пособие для вузов / Е.П. Угрюмов. – СПб.: БХВ-Петербург, 2004. – 800 с.
6. Н.А. Галанина, Д.Д. Дмитриев Синтез БПФ на ПЛИС с применением
системы остаточных классов // Программные системы и вычислительные методы. - 2013. - 1. - C. 129 - 133. DOI: 10.7256/2305-6061.2013.01.11.
References
1. Akushskii, I. Ya. Mashinnaya arifmetika v ostatochnykh klassakh / I.Ya. Akushskii, D.I. Yuditskii. – M.: Sov. radio, 1968. – 440 s.
2. Galanina, N. A. Realizatsiya blokov shifratsii i deshifratsii signalov v nepozitsionnykh ustroistvakh TsOS / N.A. Galanina, N.N. Ivanova, A.A. Ivanov // Vestnik Chuvashskogo universiteta. – 2007. – № 2. – S. 166-173.
3. Lebedev, E. K. Sposoby kodirovaniya v nepozitsionnykh vychislitel'nykh ustroistvakh / E.K. Lebedev // Proektirovanie EVM: mezhvuz. sb. nauch. trudov. – Ryazan': Izd-vo RRTI, 1992. – S. 104-109.
4. Strekalov, Yu. A. Realizatsiya arifmetiko-logicheskogo ustroistva, funktsioniruyushchego v sisteme schisleniya v ostatochnykh klassakh na PLIS / Yu.A. Strekalov // Infokommunikatsionnye tekhnologii. – 2004. – T. 2. – № 4. – S. 46-48.
5. Ugryumov, E. P. Tsifrovaya skhemotekhnika: ucheb. posobie dlya vuzov / E.P. Ugryumov. – SPb.: BKhV-Peterburg, 2004. – 800 s.
6. N.A. Galanina, D.D. Dmitriev Sintez BPF na PLIS s primeneniem
sistemy ostatochnykh klassov // Programmnye sistemy i vychislitel'nye metody. - 2013. - 1. - C. 129 - 133. DOI: 10.7256/2305-6061.2013.01.11.
Ссылка на эту статью
Просто выделите и скопируйте ссылку на эту статью в буфер обмена. Вы можете также
попробовать найти похожие
статьи
|
|





