|
ГЛАВНАЯ
> Вернуться к содержанию
Кибернетика и программирование
Правильная ссылка на статью:
Бородин А.В.
Линейные конгруэнтные последовательности максимального периода в задачах обфускации программ
// Кибернетика и программирование.
2016. № 6.
С. 1-19.
DOI: 10.7256/2306-4196.2016.6.18499 URL: https://nbpublish.com/library_read_article.php?id=18499
Линейные конгруэнтные последовательности максимального периода в задачах обфускации программ
Бородин Андрей Викторович
кандидат экономических наук
профессор, кафедра информатики и системного программирования, ФГБОУ ВПО «Поволжский государственный технологический университет»
424000, Россия, Республика Марий Эл, г. Йошкар-Ола, пл. Ленина, 3
Borodin Andrey Viktorovich
PhD in Economics
Professor, Department of Computer Science and System Programming, Volga State University of Technology
424000, Russia, respublika Marii El, g. Ioshkar-Ola, pl. Lenina, 3

|
bor@mari-el.com
|
|
 |
Другие публикации этого автора
|
|
|
DOI: 10.7256/2306-4196.2016.6.18499
Дата направления статьи в редакцию:
26-03-2016
Дата публикации:
31-10-2016
Аннотация:
Настоящая работа посвящена разработке системы практических методов защиты программного обеспечения от рефакторинга с целью снижения вероятности нарушения авторских прав на используемые алгоритмы. В качестве базового метода защиты предлагается подход, особенностью которого является использование линейных конгруэнтных последовательностей как основы для отображения порядка расположения операторов языка на требуемый функциональностью порядок выполнения программы. Предложена конкретная технология обфускации программ, написанных на скриптовых языках, в частности на Microsoft Visual Basic. Также обсуждается вариант формального понимания степени стойкости рассматриваемой системы методов. Для формального описания понятия обфускации программ и степени стойкости обфускации используется теоретико-множественный формализм. Ряд результатов теории чисел использован в работе для обоснования существования решения задачи обфускации в предлагаемой постановке для произвольной программы. Основным результатом работы является новый практический подход к обфускации программ, написанных на скриптовых языках, который в известной степени может быть обобщен на языковые системы иной природы. Также в работе продемонстрирован парадоксальный результат - обфусцированная программа может полностью соответствовать парадигме структурного программирования при сохранении заявленной степени стойкости к рефакторингу.
Ключевые слова:
вычислительная сложность, исходный код, лексический анализ, линейный конгруэнтный метод, машинный код, обфускация, рефакторинг, спагетти-код, cтруктурное программирование, VBA
УДК: 519.71
Abstract: The article is devoted to development of the system of practical methods of protection of software against refactoring for purpose of lowering probability of infringement copyright for used algorithms. As the basic method of protection offered approach, which feature is use of the linear congruent sequences as bases for morphism of an order of layout operators of programming language to the execution order of the program, required by functionality. The specific technology of an obfuscation programs written in scripting languages, in particular on Microsoft Visual Basic, is offered. Also the notation of formal understanding of a level resistance of the considered system of methods is discussed. For the formal description of concept of an obfuscation programs and a level resistance of an obfuscation used the set-theoretic formalism. Several results of the number theory is used in article for reasons for existence of the solution of the task obfuscation in the offered setting for any program. The main result of article is new practical approach to an obfuscation programs, written in scripting languages, which can be to a certain extent generalized on language systems of other nature. Also in article the paradoxical result is shown - the obfuscation code can correspond completely to a paradigm of structured programming when saving the declared level of resistance to refactoring.
Keywords: computational complexity, source code, lexical analysis, linear congruential generator, machine code, obfuscation, code refactoring, spaghetti code, structured programming, VBA
Введение Проблема защиты интеллектуальной собственности в последние годы становится все более и более актуальной. Связано это, как с взрывным ростом количества новых идей, продуктов и технологий, так и с упрощением процедур их описания и реализации. Информационные технологии здесь оказались катализатором инновационного процесса. Они предложили гигантское множество простых для пользователя инструментов поддержки инновационной деятельности и постарались, по возможности, предложить технологии защиты интеллектуальной собственности. В то же время, очевидно, что прогресс в развитии простых и удобных в эксплуатации инструментальных средств поддержки инноваций существенно опережает создание и развитие инструментария защиты интеллектуальной собственности. В ряду инструментальных средств, для которых справедливо все выше сказанное, можно отметить продуктовую линейку Microsoft Office, многие популярные продукты компаний Corel, MindJet, CA Technologies и т. д. Эти программные средства благодаря поддержке языка программирования Visual Basic for Applications (VBA) [13] взяли на себя роль метасистем – инструментов создания инноваций в области программного обеспечения со стороны прикладных специалистов, не считавших себя ранее специалистами в области программирования. Еще ярче эта ситуация прослеживается в сфере аппаратного обеспечения. Появление и развитие таких языков описания аппаратуры как Verilog [16] и VHDL [1], с одной стороны, чрезвычайно упростило и ускорило создание множества аппаратных решений, а, с другой, сделало ряд весьма сложных, интеллектуально емких (уникальных) проектов уязвимыми к несанкционированному использованию.
Некоторым препятствием на пути утечки интеллектуальной собственности в описанном контексте являются технологии обфускации. Неформально под обфускацией понимается приведение исходного текста или исполняемого кода программы к виду, сохраняющему её функциональность, но затрудняющему анализ, понимание алгоритмов работы и модификацию после декомпиляции [14]. Таким образом, разработка новых методов обфускации с различными заданными свойствами представляет значительный интерес.
Настоящая статья посвящена обсуждению нового практического метода обфускации программ, написанных на языке программирования VBA. Особенностью предлагаемого метода является использование линейных конгруэнтных последовательностей в качестве основы для отображения порядка расположения операторов языка на требуемый функциональностью порядок выполнения программы.
Формальное понимание обфускации Формализацию понятия обфускации удобно начать с рассмотрения коммутативной диаграммы, представленной на рис. 1.
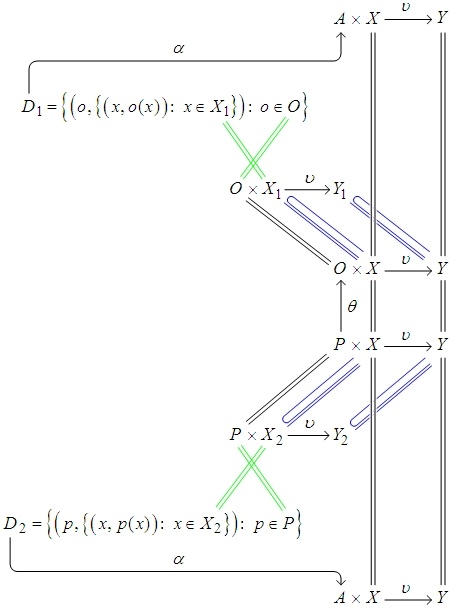
Рис. 1. Коммутативная диаграмма, иллюстрирующая понятие обфускации
На рис. 1 использованы следующие обозначения:
`P` – множество программ;
`X` – множество исходных данных для программ из множества `P` ;
`Y` – множество результатов выполнения программ из множества `P` с исходными данными из множества `X` ;
`upsilon` – отображение, реализуемое вычислителем (компьютером);
`O` – множество обфусцированных программ;
`theta` – отображение, реализуемое обфускатором (специальной программой некоторого вычислителя);
`X_1` – некоторое подмножество множества `X` , `X_1sube X` , на диаграмме это отношение представлено соответствующим удлиненным знаком синего цвета,
`Y_1` – подмножество множества `Y` , `Y_1 sube Y` , содержащее результаты выполнения обфусцированных программ из множества `O` с исходными данными из множества `X_1` ;
`D_1` – наблюдаемое атакующим субъектом множество обфусцированных программ с некоторой частью примеров их выполнения, определяемой множеством `X_1` ;
`A` – множество реконструированных атакующим субъектом программ на основе исследования элементов множества `D_1` (или `D_2` ) с использованием алгоритма реконстукции (рефакторинга), представленного на диаграмме отображением `alpha` ;
`X_2` – некоторое подмножество множества `X` , `X_2 sube X` ;
`Y_2` – подмножество множества `Y` , `Y_2 sube Y` , содержащее результаты выполнения программ из множества `P` с исходными данными из множества `X_2` ;
`D_2` – наблюдаемое атакующим субъектом множество исходных программ с некоторой частью примеров их выполнения, определяемой множеством `X_2` ;
две параллельные линии (удлиненный знак равенства) означает, что соединенные этим знаком множества – это одно и то же множество, представляемое синхронно, условно говоря, представляемое в каждый момент времени в каждой своей позиции присутствия одним и тем же своим элементом.
В связи с использованием последнего обозначения обратим внимание на отсутствие этого знака между множеством `A` , присутствующим и в верхней, и в нижней части диаграммы (это одно и то же множество, но представляемое в каждой отдельной ситуации разными своими элементами, иначе говоря, множество, представляемое на диаграмме асинхронно).
Введенная таким образом модель системы программ может быть использована для построения определения обфускации.
|
Определение 1. Алгоритм `theta` назовем обфускатором для класса программ `P` , если справедливы следующие три свойства.
1) Сохранение функциональности:
`AA p (p in P) quad AA x (x in X) quad [theta(p)(x)=p(x)]` .
2) Не более чем полиномиальное снижение эффективности:
`AA p (p in P) quad [|theta(p)| <= pi_s(|p|)]`
и/или
`AA p (p in P) quad AA x (x in X) quad [tau(theta(p)(x)) <= pi_t(tau(p(x)))]` ,
где `| p |` – сложность программы `p` по объему кода,
`pi_*` – некоторый полином,
`tau(p(x))` – время выполнения программы `p` с исходными данными `x` .
3) Стойкость к реконструкции:
`AA p (p in P) quad [tau(alpha|D_1, quadO={theta(p)}) " >> " tau(alpha|D_2, quad P={p})]` ,
где `tau(alpha|D_1, quad O={theta(p)})` – время исполнения сужения отображения `alpha` на множество `D_1` для случая, когда множество `O` содержит один элемент – результат обфускации программы `p` ,
`tau(alpha|D_2, quad P={p})` – время исполнения сужения отображения `alpha` на множество `D_2` для случая, когда множество `P` содержит один элемент – программу `p` .
|
Данное определение построено по схеме, выработанной в работах [5, 20, 25], но в терминах теории множеств. По мнению автора, предложенная нотация проще для понимания и она достаточна для постановки задачи, рассматриваемой в настоящей работе.
Заметим, что степень строгости определения 1 может быть повышена за счет уточнения смысла, вкладываемого в отношение «`">>"` », а степень специализации определения – за счет уточнения понятия отображения `alpha` и его домена. Так, например, если на рис. 1 множество исходных программ с некоторой частью примеров их выполнения `D_2` заменить на множество лишь примеров их выполнения `D_2^delta = { { (x, quad p(x)) quad : quad x in X_2} quad : quad p in P}` , а отношение «`">>"` » в третьем свойстве определения 1 понимать как отношение «`>=` », то мы приходим к определению обфускатора – «черного ящика» [20], исследование результатов работы которого предоставляет атакующему субъекту информации не больше, чем исходная программа, рассматриваемая как «черный ящик». Развитие идей, положенных в основу определения обфускатора – «черного ящика», привело к понятиям обфускатора неразличимости [20] и лучшего обфускатора [25]. Некоторые результаты в части исследования возможных практических подходов к созданию алгоритмов обфускации в названных смыслах приведены в работе [24]. Русскоязычный обзор результатов в области соответствующей теории обфускации представлен в работах [5, 7, 12]. Заметим, что во всех перечисленных публикациях в качестве нотации исследования предметной области использована теоретико-вероятностная нотация, а также язык машин Тьюринга и логических схем.
Целью настоящей работы является разработка практического метода обфускации, стойкость которого характеризуется интерпретацией отношения «`">>"` » в третьем свойстве определения 1 как простого отношения «больше». Иначе говоря, разрабатываемый метод обфускации должен усложнять полуавтоматический рефакторинг и он не претендует на строго доказанную стойкость в каком-либо смысле.
Основания разработки Разработке и исследованию практических методов обфускации посвящено огромное количество работ. Отметим некоторые из них, важные и знаковые с точки зрения данного исследования.
Очень подробный обзор практических методов обфускации дает отчет Стефана Драпе [22]. В обзорной части этого отчета, на стр. 14-16, фактически присутствует первый шаг реализации подхода, развиваемого в данном исследовании. Речь идет о статическом отображении порядка следования операторов в программе на порядок их выполнения. Остается скрыть эту статику за «ширмой» отображений, отчужденных по месту расположения в программе от функционально значимых операторов, иначе говоря, скрыть за «ширмой» динамики, реализуемой некоторой функцией, и мы получаем то, что предлагаем.
Работы [21, 23] посвящены обсуждению проблем и методов обфускации данных и, в частности, матриц. Простейшие идеи из этих двух работ эффективно могут быть использованы при обфускации констант – вспомогательного метода, способного усилить эффект разрабатываемого в данной работе подхода.
Рассматривались практические подходы к обфускации и на страницах настоящего журнала [10, 11]. Последняя из этих работ интересна упоминанием экзотических подходов к обфускации, в частности основанных на языке сетей Петри. Идеи этого подхода позволили наметить дальнейшие пути развития предлагаемого метода в направлении совместной обфускации сразу нескольких программных модулей, интерфейсный раздел которых допускает обобщение.
Идея метода Идея метода обфускации, предлагаемого в данной работе, заключается в том, что любой базовый блок программы на императивном языке программирования, см. левый столбец таблицы 1, можно представить в виде эквивалентной конструкции, см. правый столбец таблицы 1.
Таблица 1
Функционально эквивалентное преобразование базового блока программы

В таблице использованы следующие обозначения:
`g: quadNN-> NN` – биекция, которая является образующим элементом некоторой циклической группы с количеством элементов не меньше `N+1` , причем
`AA k quad (k=1, quad 2, quad ... quad, quad N+1) quad [n_i=k quad =>quad x_i=g^k(x_0)]` ,
где `g^k(x) = (@_(i=1)^k g)(x)` ;
`NN` – множество натуральных чисел;
`x_0` – некоторое начальное значение, `x_0 in NN` ;
`x_i` – значение ключа, по которому осуществляется выбор исполняемого оператора, `x_i in NN` ;
`n_i` – номер оператора, соответствующего ключу `x_i` ; `i=1, quad 2, quad ... quad, quad N+1` .
Заметим, что разные циклические образующие `g` могут порождать разные функционально эквивалентные конструкции. Дополнительное разнообразие во множество этих конструкций может внести возможность варьирования числа `x_0` . Это замечание, кстати, имеет особое значение для практики конструирования самомодифицирующихся компьютерных вирусов без сигнатур [4]. Обсуждению другой стороны этой возможности (противодействию) посвящена работа [6].
Для того, чтобы обсуждаемый подход на основе функционально эквивалентного преобразования, представленного в таблице 1, стал действительно практическим, необходимо подобрать такую биекцию `g` , которая обеспечивала бы заданный порядок порождаемой ей циклической группы и реализация которой, с одной стороны, была бы вычислительно простой, а с другой, легко бы могла быть сама подвергнута обфускации.
Хорошим кандидатом на роль такого преобразования `g` , по мнению автора, является рекуррентное соотношение, порождающее так называемые линейные конгруэнтные последовательности (ЛКП) [9]. Преобразование, порождающее ЛКП, имеет всего три параметра, соответствующий выбор которых гарантирует максимальный период последовательности, равный одному из параметров, называемому модулем, см теорему A [9, c. 29]. Поскольку период ЛКП определяет порядок циклической группы, то требование обеспечения любого заданного порядка группы выполнено. С другой стороны, ЛКП во многих случаях напоминают случайные последовательности с равномерным законом распределения элементов, что позволяет при выполнении не очень обременительных условий порождать функционально эквивалентные коды, для предположительного обнаружения экземпляра которых необходимо использовать некоторое множество сигнатур, мощность которого не меньше порядка циклической группы (периода ЛКП). Этот тезис для отрасли разработки компьютерных вирусов фактически эквивалентен следующему высказыванию: «чем больше размер кода компьютерного вируса, тем сложнее, в общем случае, делать высоко достоверный вывод о его обнаружении с использованием традиционных подходов». Проблемы, связанные с отклонением свойств ЛКП от свойств истинно случайных последовательностей, для данного приложения не вызывают проблем применимости, характерных для традиционных приложений псевдослучайных чисел, таких, как методы класса Монте-Карло и криптографические приложения [3], что также положительно характеризует наш выбор циклической образующей.
Укрупненный алгоритм метода В предыдущей главе была продемонстрирована возможность эквивалентного преобразования базового блока программы (линейного участка кода без переходов). Теперь мы рассмотрим случай, когда код содержит оператор безусловного перехода, см. таблицу 2. Нетрудно видеть, что операторы условного перехода также очень хорошо вписываются в предлагаемую модель эквивалентных преобразований.
Таблица 2
Функционально эквивалентное преобразование линейного фрагмента программы с оператором GoTo

Таким образом, мы приходим к заключению, что если некоторая программа не содержит типовых конструкций языка структурного программирования, то есть полностью представляет из себя спагетти-код [15], то она очевидным образом может быть обфусцирована предлагаемым в этой и предыдущей главах настоящей статьи методом.
Пользуясь последним замечанием можно сформулировать основные этапы предлагаемого подхода к обфускации программ:
1) лексический разбор;
2) деструктурирование кода;
3) обфускация кода;
4) обфускация переменных;
5) обфускация констант.
Из перечисленных шагов алгоритма только лексический разбор является типовым алгоритмом для данного конкретного языка программирования, на остальных этапах следует остановиться подробнее.
Деструктурирование кода В основу алгоритма деструктурирования кода положены принципы эквивалентного преобразования конструкций структурного программирования (для заданного языка программирования) в спагетти-код, см. таблицу 3.
Таблица 3
Принципы эквивалентного преобразования базовых конструкций структурного программирования языка программирования VBA


Преобразования, представленные в таблице 3, легко реализуются на основе результатов лексического разбора. При этом на первом этапе выполняются преобразования, связанные с сокращенной записью обращений к свойствам и методам объектов и классов и описанные в последней строке таблицы 3. На последующих этапах реализуется рекурсивное применение остальных преобразований таблицы 3.
Для примера рассмотрим исходный код функции, реализующей расширенный алгоритм Евклида, см. листинг 1. Этот пример будет в настоящей работе сквозным для иллюстрации всех этапов обфускации.
Листинг 1
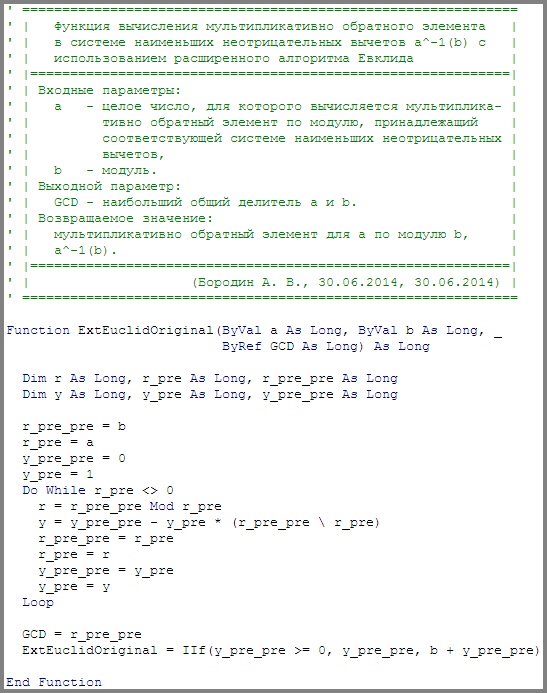
Результат деструктурирования кода, представленного на листинге1, приведен в листинге 2.
Листинг 2
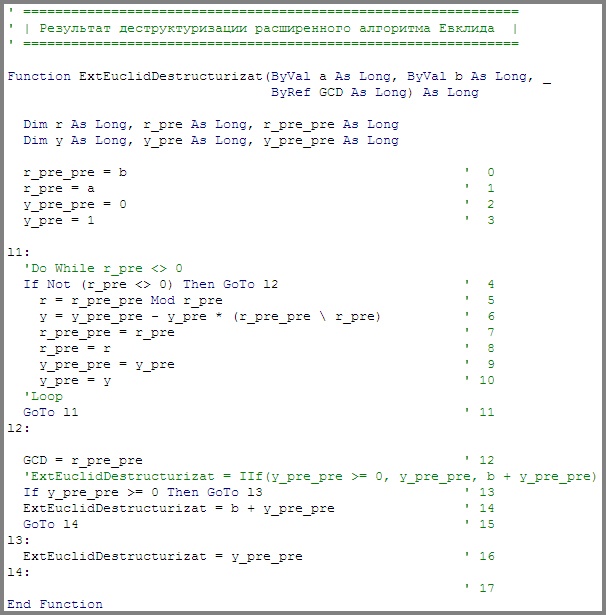
В спагетти-коде, представленном на листинге 2, сохранены отступы, позволяющие проследить прошлую структурированность программы. Также в этом коде элементы, заменившие конструкции структурного программирования, предварены комментариями, содержащими исходные элементы, а все выполнимые операторы языка пронумерованы (в заоператорных комментариях) с 0 до 16. Номер 17 соответствует выходу из функции.
Обфускация кода В программе, представленной на листинге 2, имеется 17 выполнимых операторов, пронумерованных от 0 до 16, 17-й оператор – «пустой», соответствует завершению программы. Таким образом, для обфускации программы необходима ЛКП с периодом не меньше 18. Выберем в качестве модуля линейного конгруэнтного преобразования число 18. Это означает, что преобразование `g(x)=| a x + c |_m` , где `m=18` , а `|a|_m` обозначает наименьший неотрицательный вычет числа `a` по модулю `m` , может породить ЛКП максимального периода 18, если множитель `a` и приращение `c` будут соответствовать условиям теоремы A [9, c. 29], например, `a=7` , `c=11` . В качестве начального значения `x_0` можно взять любое целое число от 0 до 17. Например, если `x_0 = 8` , то мы получаем следующий период:
`(13, quad 12, quad 5, quad 10, quad 9, quad 2, quad 7, quad 6, quad 17, quad 4, quad 3, quad 14, quad 1, quad 0, quad 11, quad 16, quad 15, quad 8) ` .
Используя эти значения и идеи преобразования кода, представленные в таблицах 1 и 2, мы можем преобразовать программный код, приведенный на листинге 2, в программный код, приведенный на листинге 3.
Листинг 3

На листинге 3 присутствуют отступы, демонстрирующие структурную организацию нового эквивалентного кода. Кроме того, добавлены строчные комментарии для «логического присутствия» меток и операторов «GoTo», а также заоператорные комментарии для номеров операторов (по порядку выполнения) и значений элементов периода, предшествующих требуемым, в соответствии с оператором «GoTo».
Как мы убедились, алгоритм преобразования оказывается очень простым.
Обфускация переменных По мнению ряда исследователей [26] проблемы с семантикой идентификаторов при рефакторинге увеличивают время, необходимое для понимания алгоритма, в среднем в два раза по отношению к ситуации, когда поток управления зависит от множества «непрозрачных» предикатов. Еще большего эффекта можно добиться при реализации идеи повторного использования идентификаторов [26], когда семантически обусловлено разные идентификаторы, но не пересекающиеся по области использования, при совпадении типов, объединяются по обфусцированному имени.
При этом, при синтезе обфусцированных идентификаторов могут применяться различные стратегии:
1) генерация имен, состоящих из допустимых случайных (псевдослучайных) символов, длиной из заданного интервала, или имен с фиксированной длиной, когда границы интервала совпадают;
2) генерация имен, состоящих из некоторого количества повторяющихся допустимых символов, в условиях, когда множество символов задано и задан интервал длин идентификаторов;
3) смешанная стратегия с равновероятным выбором стратегий 1 и 2.
В качестве примера, результат обфускации имен переменных в коде, приведенном на листинге 3, при фиксированной длине идентификаторов, равной 8, приведен на листинге 4.
Листинг 4
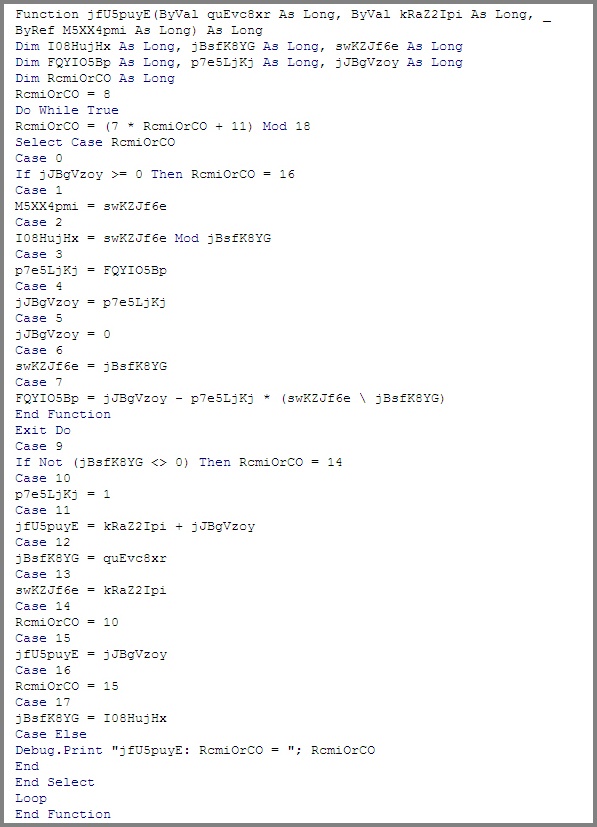
На листинге 4 отступы, демонстрирующие структурную организацию программы, и все комментарии удалены.
Таблица замены идентификаторов представлена таблицей 4.
Таблица 4
Таблица замены идентификаторов
| No |
IderOld |
IderNew |
| 1 |
ExtEuclidObfuskat1 |
jfU5puyE |
| 2 |
a |
quEvc8xr |
| 3 |
b |
kRaZ2Ipi |
| 4 |
GCD |
M5XX4pmi |
| 5 |
r |
I08HujHx |
| 6 |
r_pre |
jBsfK8YG |
| 7 |
r_pre_pre |
swKZJf6e |
| 8 |
y |
FQYIO5Bp |
| 9 |
y_pre |
p7e5LjKj |
| 10 |
y_pre_pre |
jJBgVzoy |
| 11 |
xx |
RcmiOrCO |
Обфускация констант В целом ряде случаев, знание констант, используемых в программе, способно существенно облегчить понимание семантики алгоритма. Поэтому сокрытие явного использования констант может стать одним из препятствий на пути рефакторинга программ, по крайней мере, при ручном анализе кода. Для автоматизированного анализа обфускация констант вряд ли может стать серьезным препятствием, но для непрофессионального ручного анализа она может создать заметные проблемы.
Заметим, что константы основных базовых типов языков программирования легко могут быть представлены целыми неотрицательными числами. Константа целого типа – это целое неотрицательное со знаком, вещественного типа – это целое неотрицательное со знаком для мантиссы и целое неотрицательное со знаком для порядка, константа строкового типа – это набор ординалов, соответствующих символам, иначе, набор целых неотрицательных чисел. Таким образом, задачу обфускации констант базовых типов можно свести к задаче обфускации целых неотрицательных констант.
Формализуем задачу. Пусть `C` – множество целых неотрицательных констант, используемых в обфусцируемой программе, `C sub ZZ_0^+` . Здесь `ZZ_0^+` – множество целых неотрицательных чисел. Пусть, далее, `m = max quad C quad + quad 1` , то есть `Csube ZZ_m stackrel(Def)(=) {0, quad 1, quad ... quad, quad m-1}` . Пусть `R` – множество (вспомогательных) констант, которые представлены в программе не только своими идентификаторами, но и явно записанными целыми числами без знака. Теперь можно ввести множество констант, используемых в программе и заданных явно,
`C_0(R) = C nnR` .
На первом шаге, используя данное множество констант, можно его расширить с помощью ряда линейных комбинаций:
`C_1(R, quad A_0, quad x_0)=C_0(R) quad uu quad{c: quad c in C-C_0(R), quad c=sum_(a in A_0(c)) quad x_0(c, quad a) quad a}` ,
где `A_0: quad C-C_0(R) -> 2^(C_0(R))` – некоторая функция, представляющая подмножество констант, из множества `C_0(R)` , используемых в линейной комбинации для порождения некоторых констант из множества `C-C_0(R)` на первой итерации,
`x_0: quad [C-C_0(R)] xx C_0(R) -> C_0(R)` – функция, которая при порождении некоторых констант `c` , из множества `C-C_0(R)` , сопоставляет каждому члену линейной комбинации из множества `A_0(c)` коэффициент из множества `C_0(R)` .
На последующих шагах мы можем постепенно расширять множество констант, определенных через константы предыдущих шагов:
`C_(k+1)(R, quad A_k, quad x_k) = C_k(R, quad A_(k-1), quad x_(k-1)) quad uu`
`uu quad {c: quad c in C-C_k(R, quad, A_(k-1), quad x_(k-1)), quad c=sum_(a in A_k(c)) quad x_k(c, quad a) quad a}` ,
где `A_k: quad C-C_K(R, quad A_(k-1), quad x_(k-1)) -> 2^(C_k(R, quad, A_(k-1), quad x_(k-1))` – некоторая функция, представляющая подмножество констант, из множества `C_k(R, quad A_(k-1), quad x_(k-1))` , используемых в линейной комбинации для порождения некоторых констант из множества `C-C_k(R, quad A_(k-1), quad x_(k-1))` на `(k+1)` -й итерации,
`x_k: quad [C-C_k(R, quad A_(k-1), quad x_(k-1))] xx C_k(R, quad A_(k-1), quad x_(k-1)) -> C_k(R, quad A_(k-1), quad x_(k-1))` – функция, которая при порождении некоторых констант `c` , из множества `C-C_k(R, quad A_(k-1), quad x_(k-1))` , сопоставляет каждому члену линейной комбинации из множества `A_k(c)` коэффициент из множества `C_k(R, quad A_(k-1), quad x_(k-1))` , `k=1, quad 2, quad ...` .
Очевидно, что для некоторых `R` на некоторой итерации `k'` будет достигнуто определение всех необходимых констант:
`C_(k')(R, quad A_(k'-1), quad x_(k'-1)) = C` .
Определим множество возможных параметров порождения заданного множества констант при фиксированном множестве непосредственно заданных констант:
`V(R)stackrel(Def)(=) {(k', quad (A_k, quad x_k)_(k=0)^(k=k'-1)): quad C_(k')(R, quad A_(k'-1), quad x_(k'-1))=C}` .
Теперь можно сформулировать ряд оптимизационных задач.
1) Задача минимизации количества операций при порождении заданного набора констант `C` при фиксированном множестве непосредственно определенных констант `R` :
`pi(R)stackrel(Def)(=)(k'', quad (A'_k, quad x'_k)_(k=0)^(k=k''-1))(R)=`
`="arg" quad min_(V(R)) quad sum_(k=1)^(k') quad quad sum_(c in C_k(R, quad A_(k-1), quad x_(k-1))) quad |A_k(c)|` . (1)
2) Задача минимизации количества непосредственно определенных констант среди вариантов с минимальной сложностью формул:
`R'="arg" min_(R in "Dom" quad pi) quad |R|` , (2)
где `"Dom" quad pi` – область определения функции `pi` .
Значение функции `pi(R')` можно рассматривать как оптимальную (в определенном смысле) схему обфускации констант. Следует, однако, отметить, что алгоритм точного решения задачи вычисления `pi(R')` лежит, по-видимому, в классе `"EXPSPACE"` . Поэтому на практике задача вычисления `pi(R')` решается каким-либо приближенным эмпирическим методом. Так вариант решения этой задачи для нашего сквозного примера реализован в коде, представленном на листинге 5.
Листинг 5
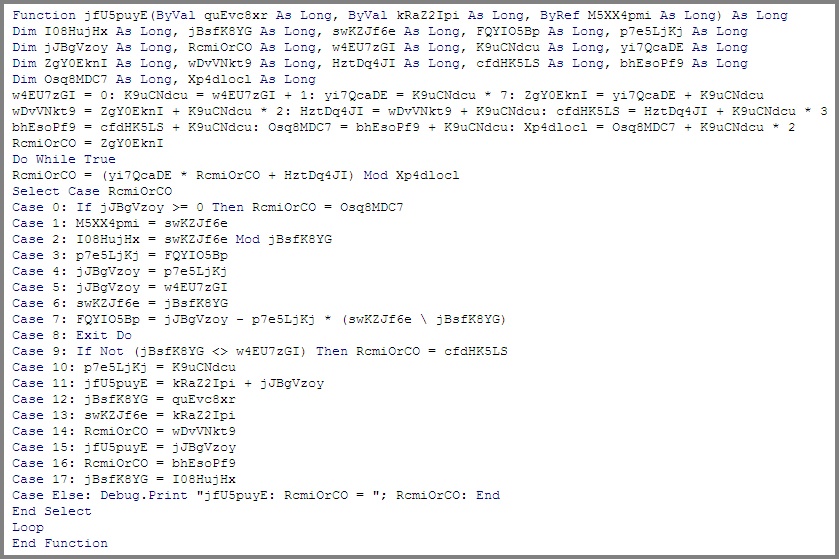
Код, представленный на листинге 5, является окончательным результатом обфускации исходного кода (листинг 1) в рамках предлагаемого подхода. Сравнив эти листинги, можно попытаться оценить перспективы соответствующего реверс-инжиниринга.
Перспективы развития Предлагаемый подход к обфускации обещает целый ряд интересных перспектив использования.
1) Предположим, что некоторое количество подпрограмм имеет одинаковый интерфейс. При этом, независимо от сложности реализации, код каждой подпрограммы может быть превращен в спагетти-код на основе идеи деструктурирования. Теперь можно вычислить суммарное количество исполнимых операторов с учетом (оператора) выхода для всех подпрограмм и построить ЛКП с соответствующей длиной периода. Если объединить эти подпрограммы под одним именем, а в их стандартный интерфейс добавить признак выбора конкретной подпрограммы и, далее, используя этот признак инициализировать `x_0` значениями из периода с шагом в длину каждой из подпрограмм, то в одну обфусцирующую конструкцию возможно уложить весь набор этих подпрограмм. Для реализации этой возможности необходимо выполнение одного дополнительного не очень обременительного (ввиду редкости возникновения прецедента) требования: объединяемые подпрограммы не должны использовать одинаковые идентификаторы для статических переменных. Очевидно, что такая смесь из кодов более чем одной подпрограммы сложнее для полуавтоматического рефакторинга, чем случай рефакторинга этих подпрограмм, обфусцированных по отдельности. И если, в случае автоматического анализа кода разделение обфусцированного кода на отдельные подпрограммы может оказаться относительно простым, то с точки зрения рефакторинга алгоритмов, использующих эти подпрограммы, такое объединение совместно с утратой семантики идентификаторов подпрограмм означает значительный рост трудоемкости [26].
2) В работе [2] был предложен метод оценки совокупной стоимости владения объектно-ориентированной метасистемой в условиях заданной модели угроз. Риск реализации угрозы в этой работе было предложено подвергнуть декомпозиции в рамках некоторой логико-вероятностной модели параллельно с декомпозицией объектной модели системы. При этом вероятность реализации активной угрозы (атаки со стороны рационального злоумышленника) здесь тем выше, чем выше степень рефакторинга целевого класса (объекта). В этом смысле предложенный подход к обфускации кода может заметно снизить вероятность реализации целенаправленной атаки. Важно, что если, с одной стороны, рост объема кода увеличивает вероятность реализации атаки, то с другой, этот же рост при применении предлагаемой технологии обфускации способен снижать эту вероятность. Таким образом, в определенных случаях, обфускация может снижать совокупную стоимость владения системами, существующими в среде некоторой объектно-ориентированной метасистемы в условиях атак, как на эти системы, так и на метасистему в целом. В этой связи отметим, что в последние годы была создана алгебраическая теория риска [17], использование методов которой позволило оценивать характеристики различных случайных величин (например, совокупной стоимости владения) с высокой степенью точности на различных интервалах времени. Таким образом, сегодня имеется возможность оценки экономической эффективности использования предлагаемого подхода к обфускации программ на заданном интервале времени в рамках использования обсуждаемой технологии в любом проектируемом приложении. Для расчетов может быть использован пакет прикладных программ (ППП) «МультиМИР» [19].
3) Часто, при исследовании программных систем, используется метод целенаправленной модификации кода с последующим изучением результатов работы модифицированного кода. Для исключения такой возможности целесообразно исследовать перспективы совместного использования предложенного подхода с технологиями доверенной загрузки программ [8].
4) В некоторых случаях предлагаемый подход может существенно усложнить реализацию некоторых позитивных педагогических идей [27]. Выход здесь просматривается в сфере более пристального внимания к программному коду работ обучающихся в части объяснения семантики алгоритмов в их тесной связи с конкретной программной реализацией.
Заключение Предложенный подход к обфускации программ был апробирован при разработке ППП «МультиМИР» версии 1.1 [18], реализованного на языке VBA, для защиты части программных модулей, содержащих элементы «know how», в связи с началом распространения данной версии ППП среди заказчиков.
В настоящее время ведутся работы по совершенствованию ряда алгоритмов предложенного метода обфускации и приведению реализации метода в состояние самостоятельного продукта.
Библиография
1. Бибило П.Н. Основы языка VHDL / П.Н. Бибило. M.: Книжный дом «ЛИБРОКОМ», 2014. 328 с.
2. Бородин А.В. Оптимизация стоимости владения объектно-ориентированной метасистемой в условиях заданной модели угроз / А.В. Бородин // Обозрение прикладной и промышленной математики. 2006. Т. 13. В. 5. С. 843–844.
3. Бородин А.В. Реконструкция и исследование датчика псевдослучайных чисел в VBA-подсистеме Microsoft Office / А.В. Бородин // NB: Кибернетика и программирование. 2014. № 4. С. 14–45. – DOI: 10.7256/2306–4196.2014.4.12648. – URL: http://e-notabene.ru/kp/article_12648.html
4. Бородин А.В. Феномен компьютерных вирусов: элементы теории и экономика существования / А.В. Бородин. Йошкар-Ола: Марийский государственный технический университет, 2004. 144 с.
5. Варновский Н.П. Математические проблемы обфускации / Н.П. Варновский, В.А. Захаров, Н.Н. Кузюрин // Труды конференции "Математика и безопасность информационных технологий" (МаБИТ-04), 28-29 октября 2004 г. М.: Московский Центр Непрерывного Математического Образования, 2004. С. 54-72.
6. Варновский Н.П. О применении методов деобфускации программ для обнаружения сложных компьютерных вирусов / Н.П. Варновский, В.А. Захаров, Р.И. Подловченко, В.С. Щербина, Н.Н. Кузюрин, А.В. Шокуров // Известия ЮФУ. Технические науки. 2006. № 7(62). С. 18-27.
7. Варновский Н.П. Современное состояние исследований в области обфускации программ: определения стойкости обфускации / Н.П. Варновский, В.А. Захаров, Н.Н. Кузюрин, А.В. Шокуров // Труды Института системного программирования РАН. 2014. Т. 26. В. 3. С. 167-198.
8. Карпов К.В. Обеспечение доверенной загрузки приложений, построенных на базе объектной модели Microsoft Excel / К.В. Карпов, А.В. Бородин // Человек, общество, природа в эпоху глобальных трансформаций: безопасность и развитие. Семнадцатые Вавиловские чтения: материалы постоянно действующей международной междисциплинарной конференции. Ч. 2. Йошкар-Ола: Поволжский государственный технологический университет, 2014. С. 252-254.
9. Кнут Д. Искусство программирования для ЭВМ. Т. 2. Получисленные алгоритмы. М.: Мир, 1977. 727 с.
10. Коробейников А.Г. Алгоритм обфускации / А.Г. Коробейников, И.М. Кутузов // NB: Кибернетика и программирование. 2013. № 3. С. 1-8. - DOI: 10.7256/2306-4196.2013.3.9356. – URL: http://e-notabene.ru/kp/article_9356.html
11. Коробейников А.Г. Анализ методов обфускации / А.Г. Коробейников, И.М. Кутузов, П.Ю. Колесников // NB: Кибернетика и программирование. – 2012. № 1. С. 31-37. – DOI: 10.7256/2306-4196.2012.1.13858. – URL: http://e-notabene.ru/kp/article_13858.html
12. Лифшиц Ю.М. Запутывание (обфускация) программ. Обзор / Ю.М. Лифшиц. СПб.: Санкт-Петербургское отделение математического института им. В. А. Стеклова РАН., 2004. – URL: http://logic.pdmi.ras.ru/~yura/of/survey1.pdf.
13. Михеев Р.Н. VBA и программирование в MS Office для пользователей / Р.Н. Михеев. СПб.: БХВ-Петербург, 2006. 384 с.
14. Обфускация (программное обеспечение) // Википедия. Свободная энциклопедия. – URL: https://ru.wikipedia.org/wiki/%D0%9E%D0%B1%D1%84%D1%83%D1%81%D0%BA%D0%B0%D1%86%D0%B8%D1%8F_(%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%BD%D0%BE%D0%B5_%D0%BE%D0%B1%D0%B5%D1%81%D0%BF%D0%B5%D1%87%D0%B5%D0%BD%D0%B8%D0%B5). Дата обращения: 28.02.2016.
15. Спагетти-код // Википедия. Свободная энциклопедия. – URL: https://ru.wikipedia.org/wiki/%D0%A1%D0%BF%D0%B0%D0%B3%D0%B5%D1%82%D1%82%D0%B8-%D0%BA%D0%BE%D0%B4. Дата обращения: 28.02.2016.
16. Стешенко В.Б. ПЛИС фирмы Altera: элементная база, система проектирования и языки описания аппаратуры / В.Б. Стешенко. М.: ДМК Пресс, 2016. 576 с.
17. Уразаева Т.А. Алгебра рисков / Т.А. Уразаева. Йошкар-Ола: Поволжский государственный технологический университет, 2013. – 209 с.
18. Уразаева Т.А. О функциональности пакета прикладных программ «МультиМИР» / Т.А. Уразаева // Современные проблемы и перспективы социально-экономического развития предприятий, отраслей, регионов. Йошкар-Ола: Поволжский государственный технологический университет, 2014. С. 261-265.
19. Уразаева Т.А. Пакет прикладных программ «МультиМИР»: архитектура и применение / Т.А. Уразаева // NB: Кибернетика и программирование. 2014. № 5. С. 34–61. – DOI: 10.7256/2306–4196.2014.5.12962. – URL: http://e-notabene.ru/kp/article_12962.html.
20. Barak, B. On the (im)possibility of obfuscating programs / B. Barak, O. Goldreich, R. Impagliazzo, S. Rudich, A. Sahai, S. Vadhan, K. Yang // Journal of the ACM. April, 2012. Vol. 59. Iss. 2. Article No. 6. 48 p. – DOI: 10.1145/2160158.2160159.
21. Drape, S. Creating transformations for matrix obfuscation / S. Drape, I. Voiculescu // Static Analysis: 16th International Static Symposium, SAS 2009. Los Angeles, CA: Springer, August, 2009. P. 273-292. – DOI: 10.1007/978-3-642-03237-0_19.
22. Drape S. Intellectual Property Protection using Obfuscation / S. Drape. Oxford: Oxford University Computing Laboratory. Wolfson Building, Parks Road, March, 2010. No. RR-10-02. 51 p. – URL: http://www.cs.ox.ac.uk/files/2936/RR-10-02.pdf.
23. Drape S. The Use of Matrices in Obfuscation / S. Drape, I. Voiculescu. Oxford: Oxford University Computing Laboratory. Wolfson Building, Parks Road, December, 2008. No. RR-08-12. 28 p. – URL: http://www.cs.ox.ac.uk/files/1851/RR-08-12.pdf.
24. Garg S. Candidate indistinguishability obfuscation and functional encryption for all circuits / S. Garg, C. Gentry, S. Halevi, M. Raykova, A. Sahai, B. Waters // 54th Annual Symposium on Foundations of Computer Science, FOCS 2013, October 2013. Berkeley: IEEE Computer Society, 2013. P. 40-49. – DOI: 10.1109/FOCS.2013.13.
25. Goldwasser, S. On best-possible obfuscation / S. Goldwasser, N. R. Guy // Fourth IACR Theory of Cryptography Conference, TCC 2007, February 21-24 2007. Amsterdam: KNAW Trippenhuis, 2007. P. 194-213.
26. Ceccato, М. A family of experiments to assess the effectiveness and efficiency of source code obfuscation techniques / M. Ceccato, M. Di Penta, P. Falcarin, F. Ricca, M. Torchiano, P. Tonella // Empirical Software Engineering. 2014. Vol. 19. Iss. 4. – P. 1040-1074. – DOI: 10.1007/s10664-013-9248-x.
27. Сидоркина И.Г., Белоусов С.А., Хукаленко К.С., Нехорошкова Л.Г. Алгоритм поиска плагиата в исходном коде программного обеспечения // Программные системы и вычислительные методы. 2013. № 3. C. 268 - 271. DOI: 10.7256/2305-6061.2013.3.9602.
References
1. Bibilo P.N. Osnovy yazyka VHDL / P.N. Bibilo. M.: Knizhnyi dom «LIBROKOM», 2014. 328 s.
2. Borodin A.V. Optimizatsiya stoimosti vladeniya ob''ektno-orientirovannoi metasistemoi v usloviyakh zadannoi modeli ugroz / A.V. Borodin // Obozrenie prikladnoi i promyshlennoi matematiki. 2006. T. 13. V. 5. S. 843–844.
3. Borodin A.V. Rekonstruktsiya i issledovanie datchika psevdosluchainykh chisel v VBA-podsisteme Microsoft Office / A.V. Borodin // NB: Kibernetika i programmirovanie. 2014. № 4. S. 14–45. – DOI: 10.7256/2306–4196.2014.4.12648. – URL: http://e-notabene.ru/kp/article_12648.html
4. Borodin A.V. Fenomen komp'yuternykh virusov: elementy teorii i ekonomika sushchestvovaniya / A.V. Borodin. Ioshkar-Ola: Mariiskii gosudarstvennyi tekhnicheskii universitet, 2004. 144 s.
5. Varnovskii N.P. Matematicheskie problemy obfuskatsii / N.P. Varnovskii, V.A. Zakharov, N.N. Kuzyurin // Trudy konferentsii "Matematika i bezopasnost' informatsionnykh tekhnologii" (MaBIT-04), 28-29 oktyabrya 2004 g. M.: Moskovskii Tsentr Nepreryvnogo Matematicheskogo Obrazovaniya, 2004. S. 54-72.
6. Varnovskii N.P. O primenenii metodov deobfuskatsii programm dlya obnaruzheniya slozhnykh komp'yuternykh virusov / N.P. Varnovskii, V.A. Zakharov, R.I. Podlovchenko, V.S. Shcherbina, N.N. Kuzyurin, A.V. Shokurov // Izvestiya YuFU. Tekhnicheskie nauki. 2006. № 7(62). S. 18-27.
7. Varnovskii N.P. Sovremennoe sostoyanie issledovanii v oblasti obfuskatsii programm: opredeleniya stoikosti obfuskatsii / N.P. Varnovskii, V.A. Zakharov, N.N. Kuzyurin, A.V. Shokurov // Trudy Instituta sistemnogo programmirovaniya RAN. 2014. T. 26. V. 3. S. 167-198.
8. Karpov K.V. Obespechenie doverennoi zagruzki prilozhenii, postroennykh na baze ob''ektnoi modeli Microsoft Excel / K.V. Karpov, A.V. Borodin // Chelovek, obshchestvo, priroda v epokhu global'nykh transformatsii: bezopasnost' i razvitie. Semnadtsatye Vavilovskie chteniya: materialy postoyanno deistvuyushchei mezhdunarodnoi mezhdistsiplinarnoi konferentsii. Ch. 2. Ioshkar-Ola: Povolzhskii gosudarstvennyi tekhnologicheskii universitet, 2014. S. 252-254.
9. Knut D. Iskusstvo programmirovaniya dlya EVM. T. 2. Poluchislennye algoritmy. M.: Mir, 1977. 727 s.
10. Korobeinikov A.G. Algoritm obfuskatsii / A.G. Korobeinikov, I.M. Kutuzov // NB: Kibernetika i programmirovanie. 2013. № 3. S. 1-8. - DOI: 10.7256/2306-4196.2013.3.9356. – URL: http://e-notabene.ru/kp/article_9356.html
11. Korobeinikov A.G. Analiz metodov obfuskatsii / A.G. Korobeinikov, I.M. Kutuzov, P.Yu. Kolesnikov // NB: Kibernetika i programmirovanie. – 2012. № 1. S. 31-37. – DOI: 10.7256/2306-4196.2012.1.13858. – URL: http://e-notabene.ru/kp/article_13858.html
12. Lifshits Yu.M. Zaputyvanie (obfuskatsiya) programm. Obzor / Yu.M. Lifshits. SPb.: Sankt-Peterburgskoe otdelenie matematicheskogo instituta im. V. A. Steklova RAN., 2004. – URL: http://logic.pdmi.ras.ru/~yura/of/survey1.pdf.
13. Mikheev R.N. VBA i programmirovanie v MS Office dlya pol'zovatelei / R.N. Mikheev. SPb.: BKhV-Peterburg, 2006. 384 s.
14. Obfuskatsiya (programmnoe obespechenie) // Vikipediya. Svobodnaya entsiklopediya. – URL: https://ru.wikipedia.org/wiki/%D0%9E%D0%B1%D1%84%D1%83%D1%81%D0%BA%D0%B0%D1%86%D0%B8%D1%8F_(%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%BD%D0%BE%D0%B5_%D0%BE%D0%B1%D0%B5%D1%81%D0%BF%D0%B5%D1%87%D0%B5%D0%BD%D0%B8%D0%B5). Data obrashcheniya: 28.02.2016.
15. Spagetti-kod // Vikipediya. Svobodnaya entsiklopediya. – URL: https://ru.wikipedia.org/wiki/%D0%A1%D0%BF%D0%B0%D0%B3%D0%B5%D1%82%D1%82%D0%B8-%D0%BA%D0%BE%D0%B4. Data obrashcheniya: 28.02.2016.
16. Steshenko V.B. PLIS firmy Altera: elementnaya baza, sistema proektirovaniya i yazyki opisaniya apparatury / V.B. Steshenko. M.: DMK Press, 2016. 576 s.
17. Urazaeva T.A. Algebra riskov / T.A. Urazaeva. Ioshkar-Ola: Povolzhskii gosudarstvennyi tekhnologicheskii universitet, 2013. – 209 s.
18. Urazaeva T.A. O funktsional'nosti paketa prikladnykh programm «Mul'tiMIR» / T.A. Urazaeva // Sovremennye problemy i perspektivy sotsial'no-ekonomicheskogo razvitiya predpriyatii, otraslei, regionov. Ioshkar-Ola: Povolzhskii gosudarstvennyi tekhnologicheskii universitet, 2014. S. 261-265.
19. Urazaeva T.A. Paket prikladnykh programm «Mul'tiMIR»: arkhitektura i primenenie / T.A. Urazaeva // NB: Kibernetika i programmirovanie. 2014. № 5. S. 34–61. – DOI: 10.7256/2306–4196.2014.5.12962. – URL: http://e-notabene.ru/kp/article_12962.html.
20. Barak, B. On the (im)possibility of obfuscating programs / B. Barak, O. Goldreich, R. Impagliazzo, S. Rudich, A. Sahai, S. Vadhan, K. Yang // Journal of the ACM. April, 2012. Vol. 59. Iss. 2. Article No. 6. 48 p. – DOI: 10.1145/2160158.2160159.
21. Drape, S. Creating transformations for matrix obfuscation / S. Drape, I. Voiculescu // Static Analysis: 16th International Static Symposium, SAS 2009. Los Angeles, CA: Springer, August, 2009. P. 273-292. – DOI: 10.1007/978-3-642-03237-0_19.
22. Drape S. Intellectual Property Protection using Obfuscation / S. Drape. Oxford: Oxford University Computing Laboratory. Wolfson Building, Parks Road, March, 2010. No. RR-10-02. 51 p. – URL: http://www.cs.ox.ac.uk/files/2936/RR-10-02.pdf.
23. Drape S. The Use of Matrices in Obfuscation / S. Drape, I. Voiculescu. Oxford: Oxford University Computing Laboratory. Wolfson Building, Parks Road, December, 2008. No. RR-08-12. 28 p. – URL: http://www.cs.ox.ac.uk/files/1851/RR-08-12.pdf.
24. Garg S. Candidate indistinguishability obfuscation and functional encryption for all circuits / S. Garg, C. Gentry, S. Halevi, M. Raykova, A. Sahai, B. Waters // 54th Annual Symposium on Foundations of Computer Science, FOCS 2013, October 2013. Berkeley: IEEE Computer Society, 2013. P. 40-49. – DOI: 10.1109/FOCS.2013.13.
25. Goldwasser, S. On best-possible obfuscation / S. Goldwasser, N. R. Guy // Fourth IACR Theory of Cryptography Conference, TCC 2007, February 21-24 2007. Amsterdam: KNAW Trippenhuis, 2007. P. 194-213.
26. Ceccato, M. A family of experiments to assess the effectiveness and efficiency of source code obfuscation techniques / M. Ceccato, M. Di Penta, P. Falcarin, F. Ricca, M. Torchiano, P. Tonella // Empirical Software Engineering. 2014. Vol. 19. Iss. 4. – P. 1040-1074. – DOI: 10.1007/s10664-013-9248-x.
27. Sidorkina I.G., Belousov S.A., Khukalenko K.S., Nekhoroshkova L.G. Algoritm poiska plagiata v iskhodnom kode programmnogo obespecheniya // Programmnye sistemy i vychislitel'nye metody. 2013. № 3. C. 268 - 271. DOI: 10.7256/2305-6061.2013.3.9602.
Ссылка на эту статью
Просто выделите и скопируйте ссылку на эту статью в буфер обмена. Вы можете также
попробовать найти похожие
статьи
|
|





