|
ГЛАВНАЯ
> Вернуться к содержанию
Историческая информатика
Правильная ссылка на статью:
Бородкин Л.И.
Сетевой анализ в исторических исследованиях: микро- макроподходы
// Историческая информатика.
2017. № 1.
С. 110-124.
DOI: 10.7256/2306-0891.2017.1.22842 URL: https://nbpublish.com/library_read_article.php?id=22842
Сетевой анализ в исторических исследованиях: микро- макроподходы
Бородкин Леонид Иосифович
доктор исторических наук
член-корреспондент РАН, профессор, заведующий кафедрой, Московский государственный университет им. М.В. Ломоносова (МГУ)
119991, Россия, г. Москва, Ломоносовский проспект, 27, корп. 4, исторический факультет МГУ
Borodkin Leonid
Doctor of History
Corresponding Member of the Russian Academy of Sciences, Professor, Head of the Department for Historical Information Science at Lomonosov Moscow State University (MSU)
119991, Russia, Moskva oblast', g. Moscow, ul. Lomonosovskii Prospekt, 27-4

|
borodkin-izh@mail.ru
|
|
 |
Другие публикации этого автора
|
|
|
DOI: 10.7256/2306-0891.2017.1.22842
Дата направления статьи в редакцию:
29-04-2017
Дата публикации:
20-05-2017
Аннотация:
Статья посвящена конкретным вопросам использования сетевого анализа в исторических исследованиях. Это сравнительно новое направление совершенствования методики и методологии исторической науки (хотя социологи рассматривают этот подход в качестве одного из ключевых с середины ХХ века). В статье рассмотрена специфика использования сетевого анализа в исторических исследованиях, которая выражается в постановке задач, особенностях структуры источников и методов их анализа. Опыт таких исследований формируется в последние годы в рамках возникшего направления Historical Network Analysis. Теоретической базой сетевого анализа является математическая теория сетей (ветвь теории графов), которая предоставляет формальный аппарат для описания структуры связей графа, его кластеров, узлов. Впервые выделяются задачи микро- и макроанализа историко-ориентированных сетей. Специальный интерес представляет задача выявления сетей индивидуумов на основе корпуса исторических текстов (типа эго-документов). В центре внимания статьи - проекты по сетевому анализу структуры средневековых русских политических и полемических текстов (при решении задач их атрибуции) и миграционных потоков в России первой четверти ХХ в.
Ключевые слова:
сетевой анализ, теория графов, матрица связи, микроанализ, макроанализ, атрибуция средневековых текстов, миграционные потоки, агрегирование, алгоритм, социальные сети
Abstract: The article addresses the issues of network analysis within historical studies. It is a comparatively new trend to modernize techniques and methodology of history (though sociology has been considering this approach as one of the main ones starting with 1950s). The article discusses the specific character of network analysis within historical studies which can bee seen in the problems set, source structure peculiarities and methods of their analysis. Such studies have been carried out within the framework of Historical Network Analysis. The theoretical basis for the network analysis is a mathematical theory of networks (a branch of graph theory) proving the formal apparatus for describing the graph links, its clusters and nodes. The goals of micro and macro analysis of history oriented networks are set for the first time. The task to find networks of individuals on the basis of historical texts (ego type documents) is a special research issue. The article focuses on the projects dealing with the network analysis of the structure of Russian medieval political and polemical texts (when the problems of their attribution are being solved) as well as migration flows in Russia in the first quarter of the 20th c.
Keywords: social networks, algorithm, aggregation, migration flows, attribution of medieval texts, macroanalysis, microanalysis, relation matrix, graph theory, network analysis
В течение последнего
десятилетия наблюдается заметный рост интереса к изучению социальных сетей
самой разной природы, прежде всего – в связи с растущей ролью электронных
коммуникаций, и, главным образом, Интернет-сетей (по М. Кастельсу, в процессе сетевизации формируется сетевое
общество). Однако уже около ста лет анализ социальных сетей развивается
социологами, рассматривающими с середины ХХ века этот подход в качестве одного
из ключевых в современной социологии. В англоязычной литературе данный социологический
подход широко известен как SNA – Social Network Analysis. В процессе развития сетевого
анализа в послевоенные десятилетия в рамках социологических исследований
формировалась теоретическая база SNA - математическая теория сетей (ветвь теории графов),
которая дает формальный аппарат для описания структуры связей графа, его
кластеров, узлов и т.д. Существующее аналитическое программное обеспечение
сетевого анализа включает модули визуализации сети.
В связи с быстрым
развитием веб-сетей, характеризующихся огромным количеством узлов и связей
между ними, непрерывным потоком разнородных сообщений, анализ таких сетей
приводит к задачам большой размерности, требующим разработки и применения
специальных алгоритмов работы с Big Data.
Теоретические и прикладные
аспекты сетевого анализа изложены в многочисленных работах социологов,
математиков, специалистов в области коммуникаций (см., например, [1],[2],[3]
[4]). Поэтому необходимости в дублировании здесь основных положений этих работ
нет. Представляет интерес, однако, рассмотрение практики использования SNA в исторических исследованиях,
которая имеет свою специфику; она выражается, прежде всего, в постановке задач,
особенностях структуры источников и методов их анализа. Этой специфике был
посвящен пленарный доклад на XVII международной конференции Ассоциации «История и
компьютер», состоявшейся в октябре 2016 г. [5].
Существующий (пока очень
скромный) опыт использования концепций SNA историками позволяет выделить,
во-первых, задачи микроанализа,
которые ставятся при работе с источником, содержащим сведения о сетях
индивидуумов; эти сведения могут быть представлены либо в явном виде (например,
при изучении личной переписки членов некоторого сообщества), либо имплицитно
(например, при изучении личных уний).
Сетевой анализ построенных графов может выявить кластеры в сложной
структуре взаимосвязей, «мосты» (индивиды, обеспечивающие соединение между кластерами), а также получить оценки центральности
(степени «влиятельности» определённого узла или кластера) и плотности сети, выявить «клики» (кластеры, в которых каждый
индивид напрямую связан с другим
индивидом), и т.д. Специальный интерес представляет задача выявления сетей
индивидуумов на основе корпуса исторических текстов (типа эго-документов). Опыт
таких исследований формируется в последние годы в рамках Historical Network Analysis (HNA). Так, в
работе [6] рассматривается задача
построения и анализа сети участников покушения на Гитлера 20 июля 1944 г. На
базе преимущественно материалов следствия по этому делу оказалось возможным
провести анализ графа связей между участниками покушения (их число превышало 200),
выявить взаимодействие различных групп: армейских генералов, дипломатов,
социал-демократов, членов профсоюзов; привлечение различных эго-документов
позволило выявить такие сетевые структуры, которые не были доступны
следователям.
Во-вторых, в практике
работы с историко-ориентированными сетями возникают и задачи макроанализа, когда источник может
содержать агрегированные, статистические сведения о связях изучаемой сети. Это
могут быть, например, данные об объеме корреспонденции между каждой парой
пунктов; интенсивности миграционных или транспортных потоков между
губерниями/областями и т.д. В этом случае сеть формализуется как взвешенный
граф, исследование которого проводится с помощью методов анализа матриц связи.
Целью такого анализа может быть выявление наиболее сильных дуг графа;
кластеров, включающих сильно связанные вершины; ядра и периферии сети и др.
* * *
Сотрудниками кафедры
исторической информатики МГУ методы сетевого анализа применяются с 1970-х гг. –
как в методически-алгоритмическом плане [7], так и в прикладном. В разное время
были реализованы проекты по сетевому анализу структуры грамматических связей в
средневековых русских текстах (при решении задач их атрибуции) [8],[9],[10], миграционных
потоков в России конца XIX – начала ХХ вв. [11],[12], историографических сетей
[13], клиентских сетей коммерческих банков дореволюционной России [14] и др.
Обзор этих работ трудно изложить в рамках одной статьи. В данной работе
рассмотрены методы, технологии и результаты более ранних исследований, дающих
примеры применения микро- и макроподходов сетевого анализа, проведенных с
участием сотрудников кафедры исторической информатики МГУ. Это позволяет
проследить отмеченную специфику сетевого анализа при рассмотрении конкретных
работ из области социально-демографической истории, а также историко-культурных
исследований. В следующей обзорной статье будет рассмотрен опыт сетевых
исследований в экономической истории и историографических исследованиях (в
рамках микроподхода).
Сетевой анализ
структуры грамматических связей
в средневековых русских
текстах
Атрибуция средневековых
русских полемических и политических произведений – одна из наиболее сложных
проблем источниковедения. Причиной тому является, прежде всего, слабость
авторского начала в произведениях той эпохи, которые до XVII в. редко имели
авторскую подпись. Задача атрибуции в данном случае требует выявления
подсознательных элементов стиля, специфики применения тем или иным автором
различных грамматических (морфологических) форм и их сочетаний. Рассмотрим
сетевой подход к решению этой задачи, основываясь на результатах исследования,
инициированного в 1970-х гг. Л.В. Миловым [8]. В рамках этого исследования автор
данной статьи предложил алгоритм, использующий теорию графов для проведения
стилометрического анализа средневековых русских политических и полемических
текстов [8],[9].
Как отмечалось в работах
ряда исследователей проблемы авторства древних и средневековых текстов, именно
частоты парной встречаемости грамматических форм слов рассматриваются как
существенные характеристики формальной структуры авторского текста. Так, В.
Фукс в своей работе, посвященной анализу стилевых характеристик библейских
текстов, отмечал, что частоты переходов для синтаксических классов слов играют
в исследованиях подлинности текстов чрезвычайно важную роль [15].
Алгоритм основан на идее
атрибуции текста, авторство которого предположительно связывается с
произведениями двух или нескольких авторов. Имея установленные образцы стиля
текстов этих авторов, можно проверить гипотезы о принадлежности атрибутируемого
текста каждому из предполагаемых авторов. С этой целью проводится сравнение матриц
частот парной встречаемости грамматических классов слов анализируемых текстов.
Алгоритм учитывает, что при большом числе n грамматических классов суммирование
незначительных различий при сравнении элементов двух матриц большого размера
приводит к тому, что небольшое число действительно важных различий
"тонет" в массе второстепенных деталей. Чтобы избежать этого, мы
положили в основу методики атрибуции построение графа "сильных
связей", конструируемого по матрице частот парной встречаемости
грамматических классов слов.
Для получения такой
матрицы необходимо: выбрать систему грамматических классов, достаточно детально
описывающую грамматические особенности языка изучаемого периода; перекодировать
последовательность слов анализируемого текста в последовательность
соответствующих обозначений грамматических классов; вычислить частоты парной
встречаемости для каждой пары классов с учетом направления развертывания текста
(слева направо), т. е. построить искомую матрицу А частот парной встречаемости на уровне грамматических классов в
данном тексте.
Мы исходим из гипотезы о
том, что стиль автора характеризуется в значительной степени его
"пристрастием" к определенным грамматическим связям, частота
появления которых в тексте высока (им соответствуют высокие значения элементов aij (i, j = 1,…,n) матрицы А). Основная же масса элементов матрицы А соответствует слабым,
несущественным статистическим связям грамматических классов; их появление в
сильной мере случайно (ведь объем исследуемых текстов ограничен). Поэтому атрибуция
должна основываться на учете существенных связей, которым соответствуют высокие
значения частот aij.
Итак, пусть
рассматривается несколько гипотез об авторстве исследуемого текста, и для
каждого предполагаемого автора имеются безусловно принадлежащие ему тексты.
Тогда алгоритм атрибуции должен включать следующие шаги.
Для каждого из имеющихся
текстов (в том числе и для исследуемого текста, подлежащего атрибуции) получаем
матрицу А частот парной встречаемости
грамматических классов (статистических связей).
Анализируя каждую
матрицу, выделяем для каждого текста совокупность грамматических связей с
высокими (т.е. превышающими некоторое пороговое значение) частотами.
При сравнении полученной
совокупности существенных связей исследуемого текста с остальными текстами определяется
автор, чей текст характеризуется наиболее близкой по некоторому критерию
совокупностью существенных грамматических связей.
Конкретизацию описанной
схемы атрибуции удобно провести, формализовав введенные понятия совокупности
существенных грамматических связей, "общеязыкового ядра", критерия
сравнения и т. д. Адекватный язык для такой формализации дает теория графов.
Как нам представляется,
достаточно подробное описание алгоритма атрибуции на языке теории графов
позволит выявить специфику историко-ориентированного
сетевого анализа.
Основным понятием для
дальнейшего изложения будет понятие графа сильных связей, с помощью которого
задается совокупность синтаксических связей с высокими частотами. Будем
обозначать такой граф G (X, V), где Х - множество вершин, а V - множество дуг
графа сильных связей. Граф сильных связей Ga (X, V) строится по матрице А следующим образом. Каждому i-му синтаксическому классу ставится в
соответствие вершина xi графа Ga (X, V). Для формирования множества V
дуг графа Ga (X, V)
назначается некоторый порог α, и тогда все связи aij (i, j = 1,...,n) оказываются
"разрезанными" на сильные aij ≥ α и слабые aij < α. Каждой
сильной связи ставится в
соответствие дуга графа Ga (X, V), идущая из вершины xi в вершину xj. Очевидно, чем больше величина порога α, тем меньше дуг содержит граф Ga (Х, V).
Пусть
построены матрица A0 частот парной встречаемости
грамматических классов для исследуемого текста и m матриц Ai (i = 1, ..., m) для
текстов, принадлежащих m известным
авторам. Задавшись некоторым порогом α,
построим графы сильной связи Gi (X, Vai) для
каждой из матриц Ai (i= 0, 1,..., m). Анализируя эти графы,
выделим "общеязыковое ядро", т. е. граф Гa, составленный
из таких дуг vi € Vai,
которые входят в множество дуг Vai не менее, чем l графов Gi (X, Vai),
i≤m. Далее произведем операцию
"удаления" полученного графа Гa из каждого графа Gi (X, Vai),
в результате чего получим графы Gi (X, Vai),
содержащие "существенные" синтаксические связи: Gi
(X, Vai) = Gi (X, Vai)
Гa (i
= 0, 1, ..., m).
Для
проверки гипотез о принадлежности исследуемого текста к одному из рассматриваемых
авторов следует в соответствии с описанным выше алгоритмом сравнить граф G0
(X, Vai) с графами Gi
(X, Vai). Учитывая специфику изучаемых текстов (в
частности, вмешательство в авторский текст переписчиков, редакторов и т. д.),
критерий для такого сравнения должен опираться не на детальное сопоставление
дуг и вершин графов G0 (X, Vai)
и Gi (X, Vai) (i=1, ..., m), а на более общие, "интегральные"
характеристики структуры этих графов.
В
данной работе критерий близости графов G0 (X, Vai)
и Gi (X, Vai) (i = 1,..,m) предлагается строить, используя понятие "узловых
вершин" этих графов (будем называть их далее узлами). Узел yi € Х определим как такую вершину графа Gi
(X, Vai) (i =
1, ...,m), в которую входит более чем β дуг. Таким образом, узлу
данного графа Gi (X, Vai)
соответствует такой грамматический класс слов, который имеет существенные связи
более чем с β классами
данного текста. Множество узлов графа Gi (X, Vai)
будем обозначать Yi.
Введем
первый критерий близости исследуемого текста к i-му тексту (i = 1, ..., m)
как отношение числа общих для данных двух текстов узлов к суммарному количеству узлов для этих двух текстов:
ρ0i=|Y0∩Yi| / |Y0UYi|, (i = 1,
..., m) (1)
Очевидно,
значение коэффициента ρ заключено в границах от 0 до 1. В том случае, если
сравниваемые тексты не имеют общих узлов, ρ = 0; если множества их узлов совпадают, ρ =1. Чем больше доля их общих узлов, тем ближе значение ρ к 1. Если для некоторого i*-гo текста значение ρoi> ρ0j (j
= 1, ..., m; j≠i*), то принимается гипотеза о принадлежности
исследуемого текста i*-му автору.
Для
описания методики выявления авторских особенностей стиля нам потребуется ввести
понятие общего графа G (X, U) для данной совокупности графов Gi (X, Vi)
(i=1,...,k). Множество дуг U общего
графа G (X, U) определим как пересечение множеств Vi (i=1,...,k): U = ∩ Vi. Таким образом, общий
граф G (X, U) построен на таких дугах, которые содержатся во всех графах Gi
(X, Vi) (i = 1, ..., k).
Введем
также второй коэффициент qi, близости каждого из графов G (X, Vi)
(i=1,..., k) к общему графу G (X, U) как отношение числа дуг, общих для графов Gi (X, Vi)
и G (X, U), к числу дуг графа Gi (X, Vi):
qi=|Vi∩U|
/ |Vi|, i = 1. ..., k. (2)
Коэффициент qi
изменяется в пределах от 0 до 1; qi=1 , если все дуги общего графа
имеются на графе Gi (X, Vi).
Для
пояснения смысла коэффициентов ρ и
q близости пары графов рассмотрим иллюстративный пример. Пусть имеются три
графа связей с множеством вершин (грамматических классов) Х={1, 2, 3, 4, 5, 6}:
Определим узел графа как
такую вершину, в которую входит не менее трех дуг. Тогда множество узлов графа
G1 составляют вершины 2 и 5, графа G2 - вершины 2 и 4, а графа G3 - 2, 5 и 3.
Перепишем формулу (1) в более простом
виде: ρ0i = nij / (ni + nj – nij) где
ni, nj - число узлов i-го
и j-го графов соответственно; nij - число общих узлов в сравниваемых графах. Легко видеть,
что вычисления по данной формуле дают для рассматриваемых графов G1,
G2, G3 следующие
значения их сходства по наборам узлов:
ρ 1,2 = 1 / (1+2-1) =1/3;
ρ 1,3 = 2 /
(2+3-2) =2/3; ρ 2,3 = 1 / (2+3-1)
=1/4.
Таким образом, наиболее близкими (по
критерию ρ) являются графы G1 и G3 .
Определим G0 - общий граф для G1,
G2 G3 :
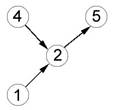
Вычисления по формуле (2)
приводят к следующим результатам сравнения структурной близости каждого из
графов G1, G2, G3 с
общим графом G0 : q1=3/8; q2=3/9; q3=3/10 . Самым близким (по
критерию q) к общему графу оказывается граф связей первого текста, самым
далеким - третьего.
Обобщив формулу (2),
можно ввести в рассмотрение коэффициент qij , измеряющий
близость структуры любой пары графов Gi и Gj как
отношение числа дуг, общих для графов Gi и Gj, к
суммарному числу различающихся дуг для рассматриваемой пары текстов:
qij=Nij / (Ni+Nj-Nij) (3)
где Ni и Nj - число дуг i-го и j-го графов соответственно; Nij - число
общих дуг в сравниваемых графах.
Вычисления по формуле (3)
дают следующие значения для сравнения структурной близости графов G1,
G2 и G3 по наборам дуг :
q12=6/(8+9-6) = 6/11; q13=5/(8+10-5) = 5/13; q23=4/(9+10-4) = 4/15.
Ближе всего по совокупности связей оказываются первый и второй
тексты, дальше всего - второй и третий.
Описанный алгоритм был реализован
автором в виде компьютерной программы, которая была апробирована в ходе анализа
нескольких произведений конца XV и XVI вв. Это три произведения Зиновия
Отенского: «Истины показание», «Похвальное слово на открытие мощей епископа
Никиты», «Слово на открытие мощей архиепископа Ионы» и два произведения Иосифа
Волоцкого: «Послание епископу Нифонту Суздальском» и «Послание Иосифа И. И. Третьякову».
Важно, что атрибуция этих текстов является общепринятой в исследовательской
литературе. Для анализа были взяты две выборки по 1000 значимых слов из
середины и конца самого большого произведения Зиновия Отенского – «Истины
показание» и по одной выборке в 1000 значимых слов из начальных разделов небольших
по объему его произведений: «Похвальное слово на открытие мощей епископа
Никиты» и «Слово на открытие мощей архиепископа Ионы», а также из начальных
разделов двух произведений Иосифа Волоцкого: «Послание епископу Нифонту
Суздальскому» и «Послание Иосифа И. И. Третьякову».
В тексте выборок был произведен
грамматический анализ слов, при котором учитывались для существительных –
падеж; для глаголов – время, лицо, инфинитив; для прилагательных – падеж, форма
(краткая или полная); для причастий – время, падеж, форма (краткость или
полнота); для местоимений – тип, падеж, а также учитывались числительные и
наречия. На основе данных характеристик была составлена таблица, в которой
каждый грамматический класс получил соответствующий кодовый номер (их общее
количество - 92). Изучаемые тексты были закодированы и представлены для
дальнейшего анализа в виде последовательности кодов. На рис. 1-4 представлены
некоторые из графов связей, выявленных в данном исследовании [8]; числа в
кружках (вершинах графов) обозначают номера грамматических классов.
Анализ структуры полученных графов,
отражающих частоты парных встречаемостей частей речи в предложениях указанных
текстов, позволил уверенно выделить те или иные части речи, являющиеся
своеобразными дистрибутивными «узлами». Совокупность окружения таких языковых
единиц широко варьируется в пределах круга произведений того или иного автора,
но центр ее постоянен. Апробация предложенного алгоритма доказала его
работоспособность в задачах атрибуции средневековых русских текстов.
В упомянутых выше работах [8],[9],[10]
показано, что, несмотря на сложность рассмотренных текстов, размытость
авторских стилевых особенностей вследствие влияния жанров и литературных
авторитетов, наличия редакторских вторжений, существуют возможности выделения
индивидуальных черт в языке отдельных авторов. Полученные с помощью теории
графов и сетевого анализа выводы в целом подтверждают гипотезу о том, что
индивидуальные авторские черты в средневековых русских произведениях
прослеживаются в особенностях расположения и связи частей речи в различных
формах в рамках предложения.
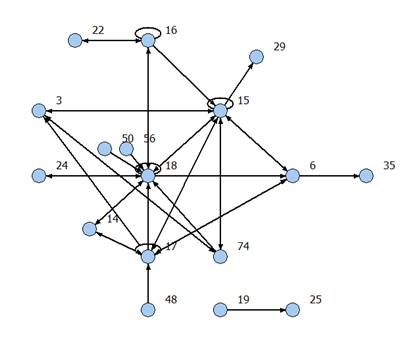
Рис. 1. Граф первой выборки из «Истины показание»
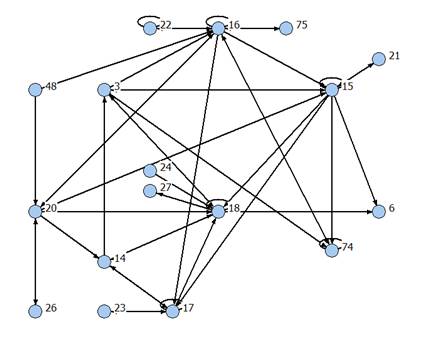
Рис. 2. Граф второй выборки из «Истины показание»
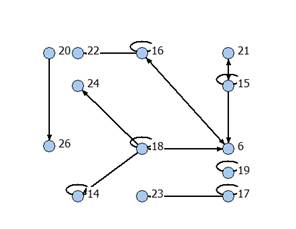
Рис. 3. Общий граф для текстов Иосифа Волоцкого
«Послания Нифонту Суздальскому» и «Послания И. И.
Третьякову»
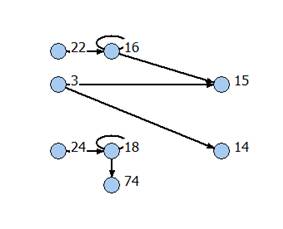
Рис. 4. Общий граф для всех произведений Зиновия Отенского
Сетевой анализ
миграционных потоков в России
конца XIX – начала ХХ вв.
Обратимся теперь к примеру
использования сетевого анализа в макро-исторических исследованиях. Речь идет о
сетевом анализе миграционных потоков; первые наши публикации по этой тематике
относятся к началу 1990-х гг. [11],[12], а затем они были продолжены в
последние годы [17],[18]. Рассматриваемый период миграций связан в истории
России с первой волной индустриализации, столыпинской реформой, войнами,
революциями. Динамизм социальных процессов эпохи выразился, в частности, в
резко возросшей миграционной активности населения, три четверти численности
которого в то время составляли крестьяне. Основным источником для проведения
сетевого анализа структуры миграционных потоков послужили сведения Всесоюзной
переписи населения 1926 г.
Полные итоги этой переписи были опубликованы в виде 56 томов. Издание включало
7 отделов. Для целей нашего исследования наибольший интерес представляет III
отдел («Семейное состояние. Место рождения и продолжительность проживания.
Увечность»), материалы которого опубликованы в 35-51-м томах. Данные об
интенсивности миграционных потоков получены на основе сводки результатов
ответов на 6-й и 7-й вопросы личного листка переписи («Где родился: здесь или
нет; если не здесь, то где и сколько времени постоянно живет здесь?»). В
таблице III отдела публикации материалов переписи («Уроженцы других районов по
месту рождения. Итоги по социальным группам») эти данные представлены в виде
матриц, содержащих показатели численности мигрантов для каждой пары регионов.
Число этих больших территорий равно 29; они соответствуют сетке госплановских
районов 1927 г.
В данной работе интерес для нас представляла матрица межрегиональных миграций
для крестьян-хозяев. Каждое число в этой матрице показывает, сколько уроженцев
одного региона постоянно проживало на момент проведения переписи в другом
регионе. Всего же перепись 1926
г. зафиксировала 3 605 314 сельских хозяев — уроженцев
других районов (т.е. переселенцев).
Для количественной оценки
интенсивности миграционных потоков в работе использовались три коэффициента,
обычно применяемых в демографических исследованиях: коэффициент прибытия (К+),
коэффициент убытия (К-) и коэффициент миграционного баланса (К).
В результате было
получено более 800 значений коэффициента К (исходя из размера матрицы 29х29),
характеризующих весь спектр теоретически возможных направлений крестьянской
миграции с территории каждого из 29 регионов.
Однако визуализация,
наглядное представление структуры миграционной сети затрудняются ввиду большого
количества незначительных межрегиональных связей на графе сети. С другой
стороны, структурное многообразие механического движения крестьянского
населения страны выразилось в примерах многократных наложений миграционных
потоков. При этом районы, сходные по структуре выезда относительно одного
направления, могли значительно различаться относительно другого. В этой связи
возникает вопрос о построении укрупненной сети миграции, где в качестве
группообразующего фактора использовалась бы структура миграционных взаимосвязей
всех 29 регионов страны. Таким образом, можно констатировать потребность в
эффективной методике, применение которой дало бы возможность построить
оптимальную укрупненную сеть, характеризующую пространственную структуру
миграций. При этом принадлежность каждого района к той или иной группе (кластеру)
определяется, исходя из общности сетевых потоков крестьянской миграции, характерных
для регионов, составивших каждую такую группу (кластер). Нами разработан алгоритм,
позволяющий решить сформулированную задачу [16]. Этот алгоритм выявления укрупненной
(агрегированной) структуры сети основан на аппроксимационном методе
агрегирования сетей (АМА), основанного на гипотезе о том, что макроструктура сети
может быть представлена в виде набора подсистем, каждая из которых состоит из
элементов, имеющих «однородные», близкие по величине связи с элементами других
подсистем. Тем самым мы переходим от исходной «калейдоскопичной» картины
связей, содержащей сотни (или тысячи) второстепенных деталей, к укрупненной
структуре сети. В результате создается возможность выявления основных потоков
связей, определения групп элементов — «поставщиков» и «потребителей», «узлов»
связей и автономных кластеров, относительно изолированных от остальных
подсистем.
Рассматриваемый метод АМА
сводится к решению экстремальной комбинаторной задачи. В итоге для заданного
числа кластеров мы получаем оптимальное разбиение элементов на кластеры (группы),
а также матрицу межгрупповых связей. Компьютерной обработке подверглась матрица
S структурных (или относительных)
коэффициентов миграции (размером 29х29), в которой каждый коэффициент sij фиксировал долю крестьян — уроженцев
i-го района, переселившихся в j-й район, относительно общего числа
крестьян - переселенцев i-го района.
Обратимся к результатам
построения структуры укрупненной сети крестьянских миграций. С помощью метода
АМА выделено восемь кластеров, состоящих из районов со схожей структурой
миграционных потоков:
1. Сибирский край;
2. Казакская АССР;
3. Северо-Кавказский край;
4. Центрально-Черноземный район, Крымская АССР,
Белорусская ССР, Полесский, Правобережный, Левобережный, Степной, Днепропетровский
и Горнопромышленный подрайоны Украинской ССР;
5. Киргизская АССР, Узбекская ССР, Туркменская ССР;
6. Дагестанская АССР, Закавказский край;
7. Якутская АССР, Бурято-Монгольская АССР,
Дальне-Восточный край;
8. Северный, Ленинградско-Карельский, Западный,
Центрально-Промышленный, Вятский, Нижне-Волжский, Средне-Волжский и Уральский
районы РСФСР, Башкирская АССР.
Обращает на себя внимание
тот факт, что каждый из пяти полученных составных кластеров состоит из
территориально смежных районов. Это позволяет рассматривать каждый такой
кластер как достаточно однородный, отдельный макрорайон, что заметно облегчает
интерпретацию полученной миграционной сети. Исходя из территориальной общности
этих макрорайонов, будем в дальнейшем именовать их следующим образом: I. Сибирский; II. Юго-Западный; III.
Северо-Кавказский; IV. Казакский; V. Средне-Азиатский; VI. Закавказский; VII.
Северо-Восточный; VIII. Центральный.
Особо отметим выделение в
миграционной макро-сети Сибири, Казакской АССР и Северного Кавказа в качестве
самостоятельных и уникальных по характеру участия в миграционных процессах
макрорайонов страны. Это представляется вполне естественным, особенно с учетом
того, что из числа крестьян, сменивших в течение исследуемого периода регион проживания,
59, 6% переселились именно в эти три региона.
Интересный материал для
интерпретации дают вычисления средних значений коэффициентов убытия,
характеризующих структуру миграционных потоков между полученными кластерами
(см. матрицу связи, табл. 1 и рис.5).
Таблица 1. Укрупненная сетевая структура межрегиональной миграции крестьян:
матрица средних значений относительных коэффициентов убытия.
|
Укрупненные регионы (кластеры) миграционной сети
|
|
|
I
|
II
|
III
|
IV
|
V
|
VI
|
VII
|
VIII
|
|
I
|
-
|
31.8
|
5.2
|
1.5
|
0.5
|
0.1
|
9.5
|
2.1
|
|
II
|
19.0
|
-
|
8.9
|
1.6
|
7.3
|
0.1
|
0.8
|
3.6
|
|
III
|
10.6
|
27.5
|
-
|
2.7
|
1.3
|
5.1
|
1.8
|
2.0
|
|
IV
|
27.5
|
14.3
|
12.3
|
3.5
|
0.3
|
0.3
|
1.7
|
1.3
|
|
V
|
1.5
|
42.4
|
3.0
|
0.8
|
14.0
|
1.3
|
0.2
|
1.7
|
|
VI
|
1.2
|
1.6
|
62.1
|
1.1
|
0.4
|
11.4
|
0.1
|
1.3
|
|
VII
|
40.9
|
2.4
|
2.5
|
0.8
|
0.1
|
0.0
|
16.6
|
1.5
|
|
VIII
|
45.4
|
9.9
|
4.1
|
0.7
|
0.2
|
0.1
|
0.8
|
4.0
|
Примечание: состав указанных восьми кластеров приводится выше.
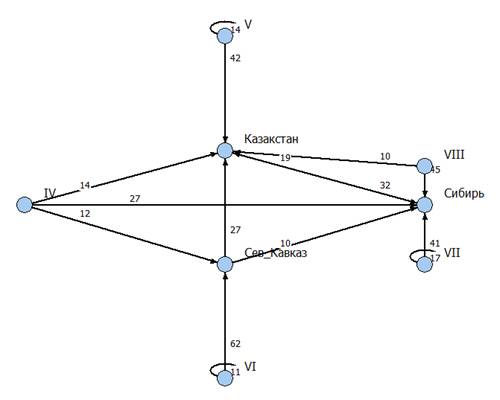
Рис. 5. Макроструктура сети
миграционных потоков крестьян в первой четверти ХХ в. (веса дуг графа имеют тот
же смысл, что и в табл. 1). На графе отражены только связи, превышающие 10%.
Если проследить
направления крестьянской миграции из трех главных макрорайонов-«потребителей» -
Сибирского, Казакского и Северо-Кавказского, то можно заметить, что крестьяне,
проживавшие раньше в этих трех регионах, но решившие по тем или другим причинам
сменить свое «благодатное» местожительство, в остальном не составляли
исключения из общего правила, продвигаясь, в первую очередь, в одном из двух
оставшихся основных направлений миграционных потоков. Крупнейший, объединяющий
большую часть территорий европейской части России Центральный макрорайон
отличает выраженная миграционная ориентация на Сибирь (в среднем 45,4% для
каждого района этой группы) при значительно меньшей, хотя и достаточно сильной,
— на Казакскую АССР (10%).
Говоря о специфике
Юго-Западного макрорайона, следует указать на бросающийся в глаза факт: данный
макрорайон последовательно вобрал в себя все территории, отмеченные наибольшим
оттоком из них крестьянских мигрантов (см. табл. 1). Именно это обстоятельство и
предопределило главную черту, присущую структуре направлений выходящих из этого
макрорайона миграционных потоков, которая выразилась в выполняемой им роли
универсального поставщика мигрантов по всем трем «генеральным» направлениям:
Сибирском (27, 5%), Казакском (14, 3%) и Северо-Кавказском (12, 3%). Подробное
изложение результатов сетевого анализа крестьянских миграций дано в упомянутых
выше публикациях [11],[12].
Отметим, что в тех
случаях, когда изучаемая сеть имеет пространственную структуру, сетевой анализ
естественным образом дополняется картографической интерпретацией. В данном
случае использование ГИС-технологий расширяет возможности пространственной
визуализации результатов сетевого анализа. Использовалась ГИС MapInfo PRO. Разработка цифровой картографической
основы была проведена на базе карты хозяйственных районов ЦСУ СССР на
23.08.1927 (не отличающейся, впрочем, высоким качеством, хотя и достаточным,
если исходить из задач визуализации структуры межрайонных миграций). Были
сформированы ГИС-слои с экспортом статистической информации и ее привязкой к
объектам карты. Эти слои включали границы 29 хозяйственных районов страны,
восьми полученных кластеров, города, направления миграций и др. [17,18]. На ГИС-карте
показаны направления и интенсивности основных крестьянских потоков миграции
между макрорайонами (Рис. 6).
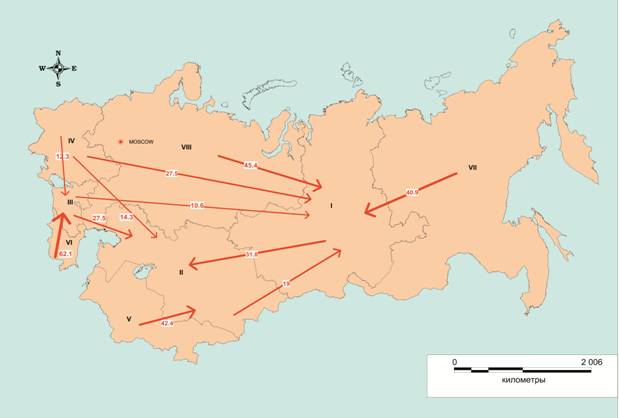
Рис. 6.
Пространственная репрезентация результатов сетевого анализа миграционных
потоков (использовалась
ГИС MapInfo PRO;
толщина стрелки и связанное с ней число характеризуют интенсивность
миграционного потока).
* * *
Методы сетевого анализа
постепенно занимают свое место в арсенале профессионального инструментария
историка. Рассмотренные в статье задачи микро- и макроанализа
историко-ориентированных сетей выявляют их специфику, которая выражается в
постановке задач, особенностях структуры источников и методов их анализа.
Сетевой анализ расширяет сферу применения в исторических исследованиях математических
методов, компьютерных моделей, востребовав методы теории графов.
Библиография
1. Hanneman R. A. and Riddle M. (2005) Introduction to social network methods. Riverside, CA: University of California, Riverside. 2005.
2. Faust K. 2005. Social networks analysis: Methods and applications. New York: Cambridge University. 2005.
3. Scott J., Carrington P. The SAGE Handbook of Social Network Analysis. Sage Publications, 2011.
4. Градосельская Г.В. Сетевые измерения в социологии. Учебное пособие. М., 2004.
5. Бородкин Л.И. Сетевой анализ в исторических исследованиях: специфика предметной области // Информационный бюллетень Ассоциации «История и компьютер» №45, 2016. С. 7-8.
6. L. von Keyserlingk. An historical network analysis on the assassination attempt of July 20 1944 // Информационный бюллетень Ассоциации «История и компьютер» №45, 2016. Международная конференция "Исторические исследования в цифровую эпоху: информационные ресурсы, методы, технологии"-XV конференция Ассоциации "История и Компьютер", Звенигород, Россия, 7-9 октября 2016. С. 134.
7. Borodkin, L. Algorithm for approximating empirical graphs-probabilistic approach // Automation and Remote Control, vol.39, № 11, 1978.
8. Л.И. Бородкин, Л.В. Милов, Л.Е. Морозова. К вопросу о формальном анализе авторских особенностей стиля в произведениях Древней Руси // Математические методы в историко-экономических и историко-культурных исследованиях / Отв. ред. И.Д. Ковальченко. М.: Наука, 1977.
9. Borodkin L., Milov L. Some Aspects of the Application of Quantitative Methods and Computers in the Analysis of Narrative Texts. In: Soviet Quantitative History / Ed. by D.K. Rowny. Sage Publications. Beverly Hills/London/New Delhi, 1984.
10. Бородкин Л.И. Математические методы и компьютер в задачах атрибуции текстов // От Нестора до Фонвизина: Новые методы определения авторства / Л. В. Милов, Л. И. Бородкин, Т. В. Иванова и др.; под ред. Л. В. Милова. М., Прогресс, 1994.
11. Бородкин Л.И., Максимов С.В. Крестьянские миграции в России/СССР в первой четверти ХХ в. (Макроанализ структуры миграционных потоков) // Отечественная история. 1993, № 5.
12. Borodkin L., Maksimov S. Network Analysis of Migration Flow Structure: The Case of Russia/USSR in the First Quarter of the 20th Century. In: The Art of Communication. Proceedings of the VIII International Conference of the Association for History and Computing. Graz,1995.
13. Гарскова И.М. Библиометрический и сетевой анализ историографии // Информационный бюллетень Ассоциации «История и компьютер», № 37, 2001.
14. Саломатина С.А. Международные корреспондентские сети московских коммерческих банков накануне Первой мировой войны // Экономическая история. Обозрение / Под ред. Л.И.Бородкина. Вып. 11. М., 2005
15. Фукс В. По всем правилам искусства (Точные методы в исследованиях литературы, музыки и изобразительного искусства) // Искусство и ЭВМ. М., 1975.
16. Borodkin, L. Algorithm for approximating empirical graphs-probabilistic approach // Automation and Remote Control, vol.39, № 11, 1978.
17. Borodkin, L. Spatial Analysis of Peasants’ Migrations in Russia/USSR in the First Quarter of the 20th Century // Information Fusion and Geographic Information Systems (IF&GIS' 2015). Springer, 2015.
18. Бородкин Л.И. Пространственная структура крестьянских переселений в России/СССР по материалам переписи населения 1926 г.: ГИС-анализ и формирование объясняющих гипотез // Информационный бюллетень Ассоциации "История и компьютер". 2015. № 43. с. 3–7.
References
1. Hanneman R. A. and Riddle M. (2005) Introduction to social network methods. Riverside, CA: University of California, Riverside. 2005.
2. Faust K. 2005. Social networks analysis: Methods and applications. New York: Cambridge University. 2005.
3. Scott J., Carrington P. The SAGE Handbook of Social Network Analysis. Sage Publications, 2011.
4. Gradosel'skaya G.V. Setevye izmereniya v sotsiologii. Uchebnoe posobie. M., 2004.
5. Borodkin L.I. Setevoi analiz v istoricheskikh issledovaniyakh: spetsifika predmetnoi oblasti // Informatsionnyi byulleten' Assotsiatsii «Istoriya i komp'yuter» №45, 2016. S. 7-8.
6. L. von Keyserlingk. An historical network analysis on the assassination attempt of July 20 1944 // Informatsionnyi byulleten' Assotsiatsii «Istoriya i komp'yuter» №45, 2016. Mezhdunarodnaya konferentsiya "Istoricheskie issledovaniya v tsifrovuyu epokhu: informatsionnye resursy, metody, tekhnologii"-XV konferentsiya Assotsiatsii "Istoriya i Komp'yuter", Zvenigorod, Rossiya, 7-9 oktyabrya 2016. S. 134.
7. Borodkin, L. Algorithm for approximating empirical graphs-probabilistic approach // Automation and Remote Control, vol.39, № 11, 1978.
8. L.I. Borodkin, L.V. Milov, L.E. Morozova. K voprosu o formal'nom analize avtorskikh osobennostei stilya v proizvedeniyakh Drevnei Rusi // Matematicheskie metody v istoriko-ekonomicheskikh i istoriko-kul'turnykh issledovaniyakh / Otv. red. I.D. Koval'chenko. M.: Nauka, 1977.
9. Borodkin L., Milov L. Some Aspects of the Application of Quantitative Methods and Computers in the Analysis of Narrative Texts. In: Soviet Quantitative History / Ed. by D.K. Rowny. Sage Publications. Beverly Hills/London/New Delhi, 1984.
10. Borodkin L.I. Matematicheskie metody i komp'yuter v zadachakh atributsii tekstov // Ot Nestora do Fonvizina: Novye metody opredeleniya avtorstva / L. V. Milov, L. I. Borodkin, T. V. Ivanova i dr.; pod red. L. V. Milova. M., Progress, 1994.
11. Borodkin L.I., Maksimov S.V. Krest'yanskie migratsii v Rossii/SSSR v pervoi chetverti KhKh v. (Makroanaliz struktury migratsionnykh potokov) // Otechestvennaya istoriya. 1993, № 5.
12. Borodkin L., Maksimov S. Network Analysis of Migration Flow Structure: The Case of Russia/USSR in the First Quarter of the 20th Century. In: The Art of Communication. Proceedings of the VIII International Conference of the Association for History and Computing. Graz,1995.
13. Garskova I.M. Bibliometricheskii i setevoi analiz istoriografii // Informatsionnyi byulleten' Assotsiatsii «Istoriya i komp'yuter», № 37, 2001.
14. Salomatina S.A. Mezhdunarodnye korrespondentskie seti moskovskikh kommercheskikh bankov nakanune Pervoi mirovoi voiny // Ekonomicheskaya istoriya. Obozrenie / Pod red. L.I.Borodkina. Vyp. 11. M., 2005
15. Fuks V. Po vsem pravilam iskusstva (Tochnye metody v issledovaniyakh literatury, muzyki i izobrazitel'nogo iskusstva) // Iskusstvo i EVM. M., 1975.
16. Borodkin, L. Algorithm for approximating empirical graphs-probabilistic approach // Automation and Remote Control, vol.39, № 11, 1978.
17. Borodkin, L. Spatial Analysis of Peasants’ Migrations in Russia/USSR in the First Quarter of the 20th Century // Information Fusion and Geographic Information Systems (IF&GIS' 2015). Springer, 2015.
18. Borodkin L.I. Prostranstvennaya struktura krest'yanskikh pereselenii v Rossii/SSSR po materialam perepisi naseleniya 1926 g.: GIS-analiz i formirovanie ob''yasnyayushchikh gipotez // Informatsionnyi byulleten' Assotsiatsii "Istoriya i komp'yuter". 2015. № 43. s. 3–7.
Ссылка на эту статью
Просто выделите и скопируйте ссылку на эту статью в буфер обмена. Вы можете также
попробовать найти похожие
статьи
|
|




